Hallar la ecuacion general de la CIRCUNFERENCIA conociendo el centro y el radio EJEMPLO 1
Summary
TLDREn este video educativo, el presentador guía a los espectadores a través del proceso de encontrar la ecuación general de una circunferencia, sabiendo su centro y radio. Se explica cómo utilizar la ecuación canónica (x-h)² + (y-k)² = r² y reemplazar los valores correspondientes. Luego, se resuelven los cuadrados de los binomios y se simplifica la ecuación hasta obtener la forma general ax² + by² + dx + ey + f = 0. El video es parte de un curso completo sobre ecuaciones de circunferencias y se anima a los espectadores a suscribirse y explorar más contenido en el canal.
Takeaways
- 📘 La ecuación canónica de una circunferencia cuando se conoce el centro y el radio es (x-h)² + (y-k)² = r².
- 🔢 Se utilizan las coordenadas del centro (h, k) y el radio r para formar la ecuación canónica.
- 📐 Para obtener la ecuación general, se expande y se resuelve el cuadrado de los binomios.
- ✅ Se resuelve el cuadrado de un binomio siguiendo la fórmula (primero)² + 2*(primero)*(segundo) + (segundo)².
- 🔄 Se manejan los signos correctamente al expandir los binomios, recordando que el producto de dos negativos es positivo.
- 📉 Se reemplazan los valores de h, k y r en la ecuación canónica para obtener la ecuación general.
- 🔢 Se realizan operaciones algebraicas para simplificar la ecuación hasta obtener la forma general x² + y² + Dx + Ey + F = 0.
- ➡️ Se organiza la ecuación general siguiendo el orden: términos cuadráticos, términos lineales y constante.
- 🔄 Se traspasan los términos para que la ecuación quede en la forma estándar x² + y² + Dx + Ey + F = 0.
- 🎓 El vídeo ofrece un ejemplo práctico para ilustrar cómo se obtiene la ecuación general de una circunferencia.
Q & A
¿Qué es la ecuación canónica de una circunferencia?
-La ecuación canónica de una circunferencia es de la forma \( (x - h)^2 + (y - k)^2 = r^2 \), donde \( h \) y \( k \) son las coordenadas del centro y \( r \) es el radio.
¿Cómo se encuentran los valores de \( h \), \( k \) y \( r \) en la ecuación canónica?
-Los valores de \( h \) y \( k \) se obtienen directamente del centro de la circunferencia, y \( r \) es el radio que se conoce previamente.
¿Qué es la ecuación general de una circunferencia?
-La ecuación general de una circunferencia es \( x^2 + y^2 + Dx + Ey + F = 0 \), donde \( D \), \( E \) y \( F \) son constantes que dependen de la posición y tamaño de la circunferencia.
¿Cómo se obtiene la ecuación general de una circunferencia a partir de la canónica?
-Para obtener la ecuación general, se expande y se resuelve la ecuación canónica, \( (x - h)^2 + (y - k)^2 = r^2 \), reemplazando y resolviendo los términos cuadrados y binomios.
¿Qué es el producto notable del cuadrado de un binomio?
-El producto notable del cuadrado de un binomio es \( (a - b)^2 = a^2 - 2ab + b^2 \), que se utiliza para expandir los términos en la ecuación canónica.
¿Cuál es el resultado de \( 3^2 \) en el ejemplo proporcionado?
-El resultado de \( 3^2 \) es 9, ya que \( 3 \times 3 = 9 \).
¿Cómo se resuelven los signos en la ecuación general de una circunferencia?
-Los signos en la ecuación general se mantienen consistentes con los de la ecuación canónica, donde los términos con signo negativo se mantienen negativos y los positivos, positivos.
¿Qué significa el término constante en la ecuación general de una circunferencia?
-El término constante en la ecuación general, que se obtiene tras expandir y simplificar, representa el desplazamiento de la ecuación con respecto al origen.
¿Cómo se determina si una ecuación representa una circunferencia y no una parábola o una línea?
-Una ecuación representa una circunferencia si tiene la forma \( x^2 + y^2 + Dx + Ey + F = 0 \) con \( D^2 + E^2 - 4F > 0 \), lo que garantiza que la ecuación describe una circunferencia y no otra curva.
¿Por qué es importante ordenar los términos en la ecuación general de una circunferencia?
-Es importante ordenar los términos en la ecuación general para que coincida con la forma estándar, lo que facilita la identificación de los coeficientes y la interpretación geométrica de la circunferencia.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Hallar la ecuación general de la CIRCUNFERENCIA conociendo el centro y el radio EJEMPLO 2

Ecuación de la circunferencia con centro fuera del origen (tercera parte).

Circunferencias: De general a ordinaria | Matemáticas | Khan Academy en Español

Find center and radius of circumference (completing perfect square trinomial)
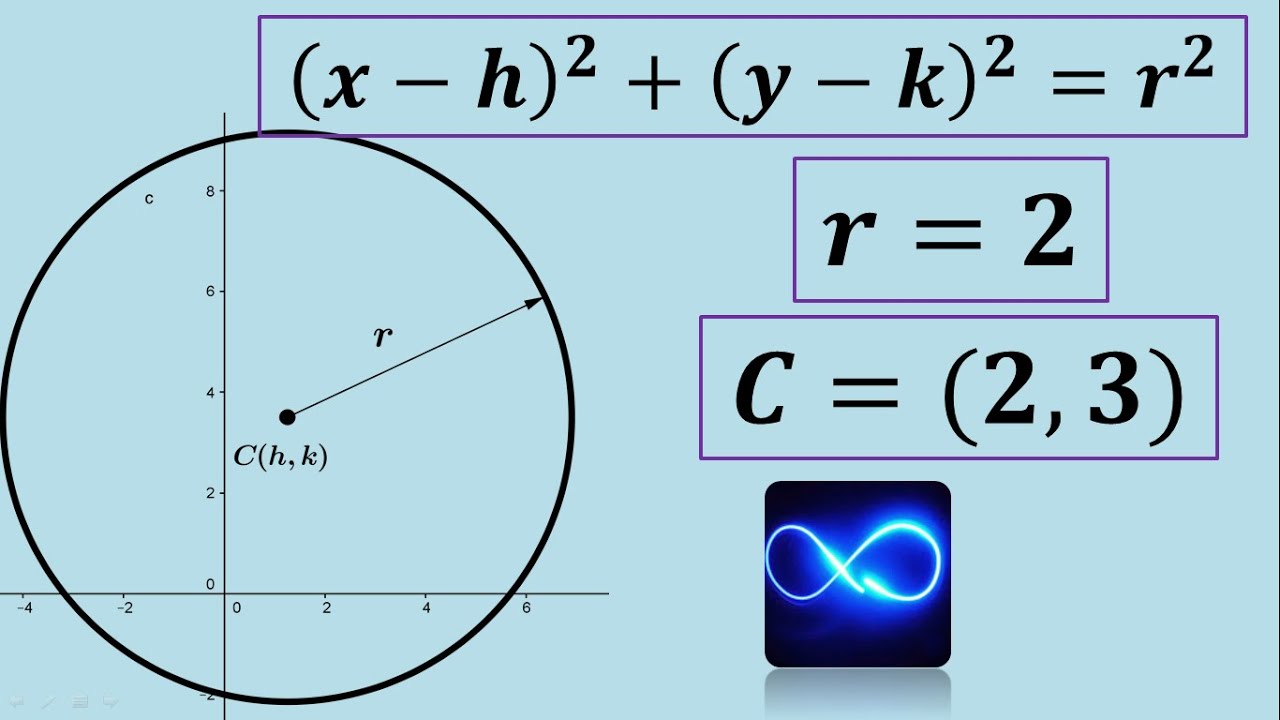
Ordinary and general equation of circumference with given center and radius (Example 1)

Ejercicio 4 de Circunferencia
5.0 / 5 (0 votes)
