Introduction to Probability, Basic Overview - Sample Space, & Tree Diagrams

Summary

This lesson delves into the concept of probability, defining it as the likelihood of an event occurring, calculated as the ratio of favorable outcomes to total possible outcomes. It introduces the sample space, the set of all possible outcomes, using coin flips as examples to illustrate how to determine the sample space for different numbers of coin tosses. The video explains how probabilities range from 0 (impossible) to 1 (certain), and provides practical examples, such as flipping coins and rolling dice, to demonstrate how to calculate probabilities for various events. It concludes with a guide to further explore topics like conditional probability and mutually exclusive events.

Takeaways

• 📚 Probability is a measure of the likelihood of an event occurring, calculated as the number of favorable outcomes divided by the total possible outcomes.
• 🎰 The sample space represents all possible outcomes of an experiment, such as flipping a coin or rolling a die.
• 🌳 A tree diagram is a useful tool for visualizing the sample space when multiple events are combined, like flipping multiple coins.
• 🔢 Probability values range from 0 (impossible event) to 1 (certain event), and can be expressed as percentages or decimals.
• 🚗 Example: The probability of selecting a person who drives a blue car from a population is 0.20, meaning 20 out of 100 randomly selected people might drive a blue car.
• 🎯 When flipping two coins, the probability of getting at least one head is 0.75, as there are three favorable outcomes (HH, HT, TH) out of four possible outcomes.
• 🎲 For flipping three coins, the probability of getting at least two tails is 0.5, with four favorable outcomes (TTH, THT, HTT, TTT) out of eight possible outcomes.
• 🎯 The probability of getting exactly one tail when flipping three coins is 0.375, with three favorable outcomes (HTH, THH, HHT) out of eight possible outcomes.
• 🎯 When tossing a six-sided die, the probability of rolling a specific number like '2' is 1/6 or approximately 16.7%, as there is one favorable outcome out of six possible outcomes.
• 📈 Probability calculations can be applied to various scenarios, including conditional, independent, and mutually exclusive events, which are covered in more detail in the speaker's statistics playlist.

Q & A

What is the definition of probability?

Probability is a measure of the likelihood that a particular event will occur. It is calculated as the number of favorable outcomes divided by the total number of possible outcomes.

What is meant by the term 'sample space' in the context of probability?

The sample space refers to the set of all possible outcomes that can occur in a given situation or experiment.

If you toss a fair coin, what is the sample space?

The sample space for tossing a fair coin is {Heads, Tails}, as there are only two possible outcomes: getting a head or getting a tail.

How many possible outcomes are there when flipping two coins?

When flipping two coins, there are four possible outcomes: HH (Heads-Heads), HT (Heads-Tails), TH (Tails-Heads), and TT (Tails-Tails).

What is the probability of getting at least one head when flipping two fair coins?

The probability of getting at least one head when flipping two fair coins is 3/4 or 75%, as there are three favorable outcomes (HH, HT, TH) out of four possible outcomes.

What is the sample space for flipping three coins?

The sample space for flipping three coins consists of eight possible outcomes: HHH, HHT, HTH, HTT, THH, THT, TTH, and TTT.

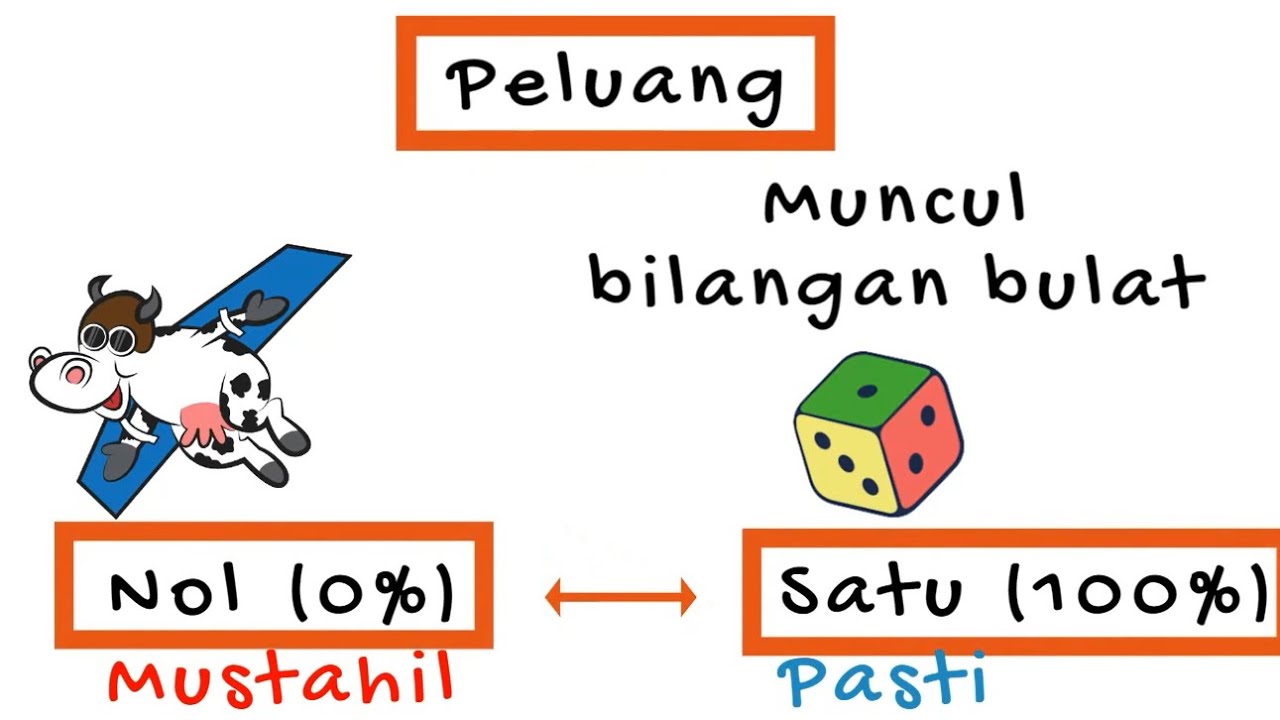
What is the probability range for any event?

The probability of an event is always between 0 and 1, where 0 means the event cannot happen and 1 means the event will always happen.

If the probability of an event is 0.3, what does this imply?

A probability of 0.3 implies that there is a 30% chance of the event occurring, meaning that out of 100 trials, approximately 30 would result in the event happening.

What is the probability of getting exactly one tail when flipping three coins?

The probability of getting exactly one tail when flipping three coins is 3/8 or 37.5%, as there are three favorable outcomes (HTH, THH, HHT) out of eight possible outcomes.

How can you calculate the probability of rolling a two with a six-sided die?

The probability of rolling a two with a six-sided die is 1/6 or approximately 16.7%, as there is only one favorable outcome (rolling a two) out of six possible outcomes.

What is the probability of rolling a number greater than three on a six-sided die?

The probability of rolling a number greater than three on a six-sided die is 1/2 or 50%, as there are three favorable outcomes (rolling a four, five, or six) out of six possible outcomes.