Simplifying Rational Expressions
Summary
TLDRThis lesson focuses on simplifying rational expressions by factoring and canceling common factors. The instructor demonstrates how to simplify expressions like 35x^5/49x^2 by reducing and subtracting exponents. Techniques for factoring out the greatest common factor (GCF) and using the difference of squares are explained. Examples include simplifying expressions with polynomials and factoring trinomials. The lesson concludes with practice problems to reinforce the concepts of factoring, taking out the GCF, and canceling to achieve the simplest form of rational expressions.
Takeaways
- 📘 Simplifying rational expressions involves reducing terms and cancelling common factors.
- 🔢 To simplify expressions with exponents, divide the coefficients and subtract the exponents of like bases.
- 📉 Factoring is a crucial step in simplifying expressions, especially when dealing with polynomials.
- 🔄 When simplifying, look for opportunities to cancel out common factors in both the numerator and the denominator.
- 📐 The greatest common factor (GCF) is often used to simplify expressions by dividing both the numerator and the denominator by it.
- ➗ In expressions with unlike terms, factoring out a negative one can help in simplifying and cancelling terms.
- 🔴 The difference of squares technique is useful for factoring expressions of the form x^2 - a^2 into (x + a)(x - a).
- 🔵 Factoring trinomials involves finding two numbers that multiply to the constant term and add up to the linear coefficient.
- 🎯 Practice is key to mastering the simplification of rational expressions, as demonstrated by the various examples provided.
- 📌 The process of simplifying rational expressions includes factoring, taking out the GCF, and cancelling common terms.
Q & A
What is the primary focus of the lesson described in the transcript?
-The primary focus of the lesson is simplifying rational expressions.
How does the process of simplifying the expression 35x^5/49x^2 begin?
-The process begins by reducing 35 and 49 by their greatest common divisor, which is 7.
What is the final simplified form of the expression 35x^5/49x^2?
-The final simplified form of the expression is 5x^3/7.
What mathematical property allows for the subtraction of exponents when dividing like bases?
-When dividing like bases, the property of subtracting exponents is used because it follows the rule of exponents which states that a^m / a^n = a^(m-n) when a is not zero.
In the example 4x^2 + 8x divided by 3x + 6, what is the first step in simplifying the expression?
-The first step is to factor out the greatest common factor (GCF) from the terms in the numerator and the denominator.
What is the final simplified form of the expression (4x^2 + 8x)/(3x + 6) after factoring and canceling?
-The final simplified form is 4x/3 after canceling the common factors.
How is the expression x^2 - 16 factored in the lesson?
-The expression x^2 - 16 is factored using the difference of squares technique, resulting in (x + 4)(x - 4).
What is the importance of factoring completely when simplifying rational expressions?
-Factoring completely is important to identify all possible common factors that can be canceled out, leading to the simplest form of the expression.
In the context of the lesson, what does GCF stand for and why is it significant?
-GCF stands for Greatest Common Factor, and it is significant because identifying and factoring out the GCF is a key step in simplifying expressions by canceling out common factors.
What is the strategy for simplifying the expression 5 - x/x - 5 as described in the transcript?
-The strategy involves factoring out a negative one from the numerator, which changes the signs of the terms and allows for the cancellation of (x - 5) in the numerator and denominator, resulting in the simplified answer of -1.
How does the lesson demonstrate the simplification of the expression 72x^8y^7/64x^5y^4?
-The lesson demonstrates the simplification by first expressing each term as a product of its prime factors, then canceling out the common factors (8, x^5, and y^4) to arrive at the simplified form of 9x^3y^3/8.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

MULTIPLICATION AND DIVISION OF RATIONAL ALGEBRAIC EXPRESSIONS || GRADE 8 MATHEMATICS Q1
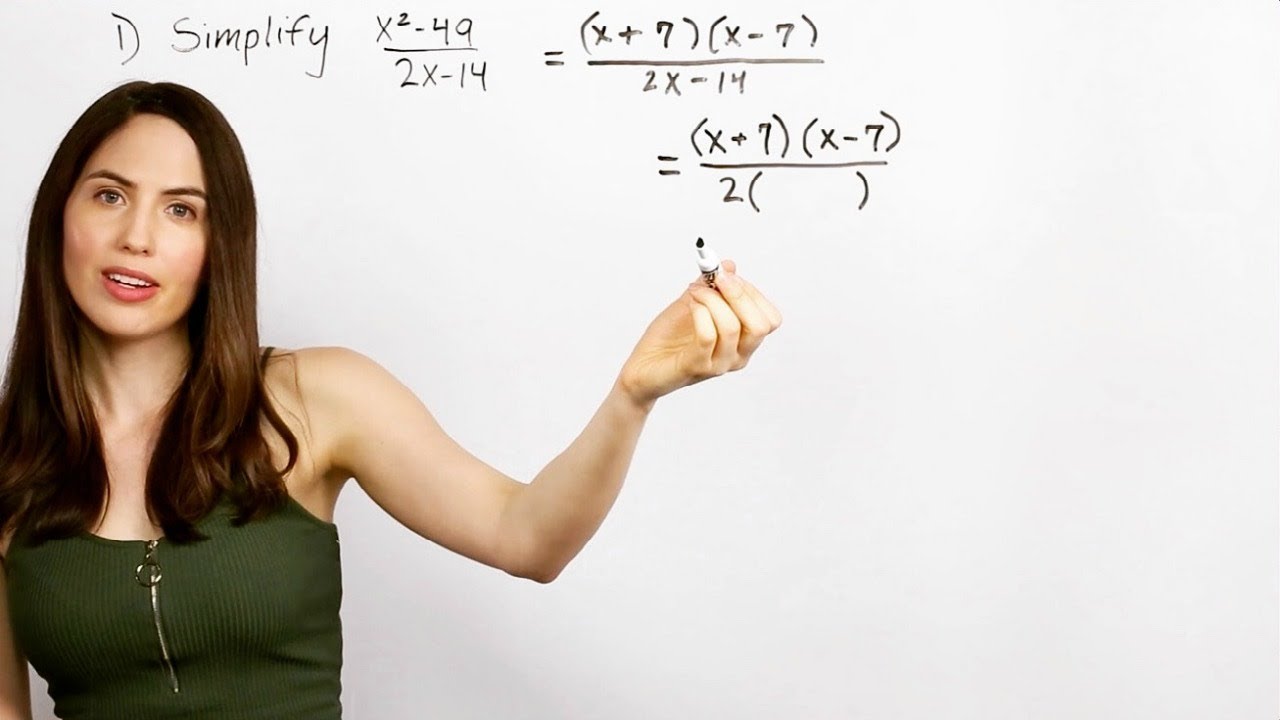
Simplifying Rational Expressions... How? (NancyPi)

Multiplying Rational Expressions

Adding and Subtracting Rational Expressions With Unlike Denominators

Solving Rational Equations

SIMPLIFYING RATIONAL ALGEBRAIC EXPRESSION || GRADE 8 MATHEMATICS Q1
5.0 / 5 (0 votes)
