El problema de la recta tangente.
Summary
TLDREl problema de la recta tangente fue crucial en el desarrollo del cálculo en el siglo 17. Se destacaron matemáticos como Newton y Leibniz, quienes trabajaron en la aproximación de la pendiente de la recta tangente a una curva en un punto específico. La solución general se basa en el uso de la recta secante, que pasa por dos puntos de la curva, y cuya pendiente se hace más precisa a medida que el segundo punto se acerca al punto de tangencia. La definición de tangente se complica en curvas no circulares, pero la pendiente de la tangente se calcula a través del límite del cociente de diferencias cuando estos tienden a cero, proporcionando una aproximación precisa de la curva en el punto de interés.
Takeaways
- 📚 El problema de la recta tangente fue un tema central en el desarrollo del cálculo en el siglo 17.
- 👨🔬 Pierre de Fermat, René Descartes, Christiaan Huygens, Isaac Barrow y otros matemáticos contribuyeron a soluciones parciales del problema.
- 🌟 La primera solución general del problema de la recta tangente se atribuye a Isaac Newton y a Gottfried Wilhelm Leibniz.
- 🔍 Newton trabajó en este problema influenciado por su interés en la refracción de la luz y la óptica.
- 📐 En una circunferencia, la recta tangente en un punto es perpendicular al radio que pasa por ese punto.
- 🤔 Para curvas generales, definir la recta tangente se vuelve más complicado y no siempre se ajusta a las definiciones simples.
- 📈 La pendiente de la recta tangente en un punto se puede aproximar usando la pendiente de la recta secante que pasa por ese punto y otro punto cercano.
- 📊 A medida que los puntos utilizados para la recta secante se acercan al punto de tangencia, la aproximación a la pendiente de la recta tangente se vuelve más precisa.
- 💡 La definición formal de la recta tangente con pendiente 'm' se basa en el límite del cociente de incrementos cuando delta x tiende a cero.
- 📖 La recta tangente a una función en un punto dado es aquella que pasa por ese punto y tiene una pendiente igual al límite del cociente de diferencias de 'y' sobre 'x'.
Q & A
¿Cuáles fueron los cuatro problemas que impulsaron el desarrollo del cálculo en el siglo 17?
-Los cuatro problemas fueron: 1) El problema de la recta tangente, 2) El problema de la velocidad y la aceleración, 3) El problema de los máximos y mínimos, 4) El problema del área.
¿Qué es el problema de la recta tangente y cómo se relaciona con el cálculo?
-El problema de la recta tangente consiste en aproximar la pendiente de la recta tangente a una gráfica en un punto dado. Se determina la pendiente de la secante que va de un punto de la gráfica a otro punto, y a medida que este segundo punto se acerca al punto dado, la aproximación se vuelve más exacta.
¿Quiénes fueron algunos de los matemáticos que contribuyeron a las soluciones parciales del problema de la recta tangente?
-Pierre de Fermat, René Descartes, Christiaan Huygens e Isaac Barrow fueron algunos de los matemáticos que propusieron soluciones parciales al problema de la recta tangente.
¿A quién se le atribuye generalmente la primera solución general al problema de la recta tangente?
-La primera solución general al problema de la recta tangente se suele atribuir a Isaac Newton y a Gottfried Wilhelm Leibniz.
¿De qué manera el interés de Isaac Newton por la refracción de la luz y la óptica influyó en su trabajo sobre la recta tangente?
-El trabajo de Newton sobre la recta tangente se originó de su interés en la refracción de la luz y la óptica. Esto lo llevó a definir la recta tangente en una circunferencia como la recta perpendicular al radio que pasa por el punto de tangencia.
¿Cómo se complica el problema de definir la recta tangente en curvas generales más allá de las circunferencias?
-En curvas generales, el problema se complica porque no es tan claro cómo definir las rectas tangentes, ya que pueden tocar la curva en el punto de tangencia sin cruzarla, o pueden cruzarla en más de un punto.
¿Cómo se puede aproximar la pendiente de la recta tangente a una curva en un punto dado?
-La pendiente de la recta tangente se puede aproximar usando la recta secante que pasa por el punto de tangencia y otro punto cercano de la curva. A medida que el segundo punto se acerca al punto de tangencia, la aproximación se vuelve más precisa.
¿Cuál es la definición formal de la recta tangente con pendiente 'm' en un punto 'c' de una función?
-Si una función está definida en un intervalo abierto que contiene 'c', y existe el límite de (f(c + Δx) - f(c)) / Δx al tender Δx a cero, entonces ese límite es igual a 'm'. La recta que pasa por el punto (c, f(c)) y tiene pendiente 'm' es la recta tangente a la gráfica de la función en el punto (c, f(c)).
¿Cómo se relaciona la pendiente de la recta tangente con la pendiente de la gráfica de una función en un punto específico?
-La pendiente de la recta tangente en un punto 'c' de la gráfica de una función se llama también pendiente de la gráfica de la función en x igual a 'c'. Esta pendiente representa la tasa de cambio instantánea de la función en ese punto.
¿Qué implica la aproximación de la pendiente de la recta tangente tomando puntos más cercanos al punto de tangencia?
-Tomar puntos más cercanos al punto de tangencia para aproximar la pendiente de la recta tangente implica que la aproximación se vuelve más precisa, ya que el cambio en 'y' se ajusta más estrechamente al cambio en 'x' en el punto de tangencia.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA, CÁLCULO DIFERENCIAL

¿Qué es la derivada? EXPLICACIÓN DESDE CERO

PENDIENTE DE LA RECTA TANGENTE: METODO DERIVADA DE LOS 4 PASOS.

Razón de cambio promedio e instantaneo
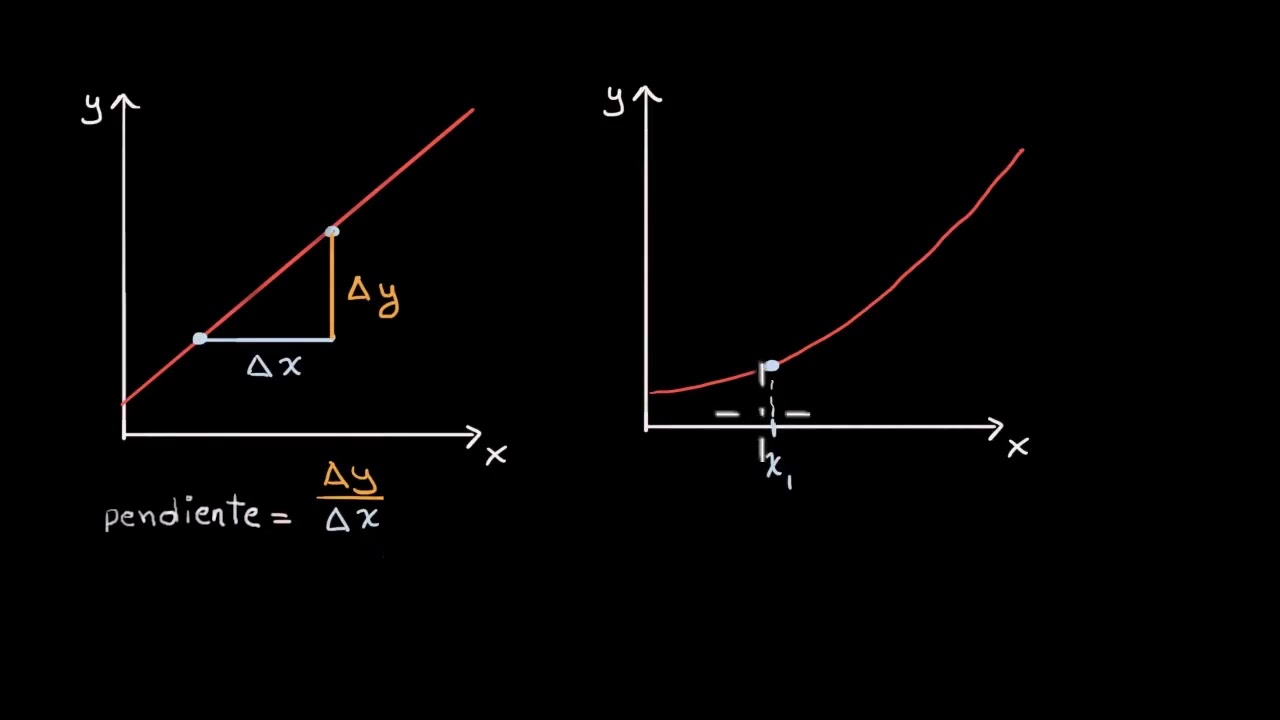
El concepto de derivada | Khan Academy en Español

NEWTON vs. LEIBNIZ: El descubrimiento del CÁLCULO infinitesimal
5.0 / 5 (0 votes)
