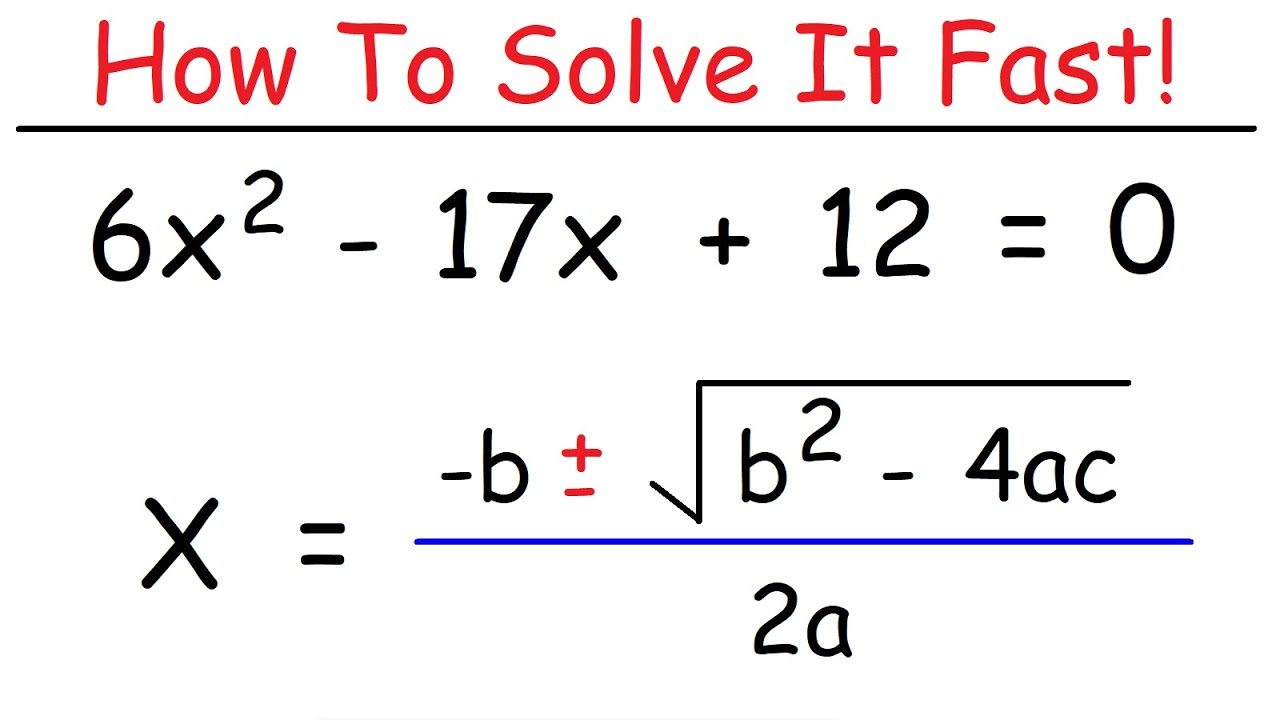MATH9 DISCRIMINANT and NATURE OF ROOTS of quadratic equation #math9 #discriminant #natureofroots
Summary
TLDRThis video tutorial in Tagalog offers a comprehensive guide on understanding quadratic equations. It explains how to calculate the discriminant using the formula B^2 - 4AC to determine the nature of the roots of a quadratic equation. The presenter walks through various examples, illustrating how to identify the values of a, b, and c from standard form equations and apply them to find the discriminant. The video clarifies that a discriminant of zero indicates real and equal roots, a positive value suggests rational or irrational roots depending on whether it's a perfect square, and a negative value implies imaginary roots. The tutorial is designed to help viewers grasp the fundamental concepts of quadratic equations and their roots.
Takeaways
- 📘 The tutorial focuses on explaining quadratic equations in Tagalog, aiming to teach the calculation of the discriminant and the determination of the nature of roots.
- 🔢 The discriminant is a crucial formula, represented as \( b^2 - 4ac \), used to determine the nature of roots in a quadratic equation.
- 🌐 There are four possible natures of roots for a quadratic equation: real and equal, rational and unequal, irrational and unequal, and no real roots or imaginary.
- 📝 The tutorial presents a step-by-step approach to solving different quadratic equations, emphasizing the importance of identifying the values of a, b, and c from the equation.
- 📉 The nature of roots is determined by the value of the discriminant: real and equal if the discriminant is 0, rational and unequal if the discriminant is a perfect square greater than 0, irrational and unequal if the discriminant is greater than 0 but not a perfect square, and imaginary if the discriminant is less than 0.
- 📑 The tutorial provides examples of quadratic equations in standard form and non-standard form, highlighting the need to manipulate the equation to standard form before applying the discriminant formula.
- 🧮 Calculation of the discriminant involves substituting the values of a, b, and c into the discriminant formula and simplifying the expression.
- 📌 The tutorial emphasizes that the values of a, b, and c must be correctly identified from the quadratic equation for accurate discriminant calculation.
- 📐 The tutorial concludes with a summary of the nature of roots for each example, reinforcing the understanding of how the discriminant affects the roots of a quadratic equation.
- 👍 The presenter encourages viewers to like and subscribe to the channel if they found the tutorial helpful.
Q & A
What is the main topic of the video?
-The main topic of the video is explaining how to calculate the discriminant of a quadratic equation and determine the nature of its roots in Tagalog.
What is the formula for the discriminant of a quadratic equation?
-The formula for the discriminant of a quadratic equation is given by "b^2 - 4ac".
What are the four natures of roots for a quadratic equation?
-The four natures of roots for a quadratic equation are: 1) Real and equal if the discriminant is equal to zero, 2) Rational and unequal if the discriminant is greater than zero and a perfect square, 3) Irrational and unequal if the discriminant is greater than zero but not a perfect square, and 4) No real roots or imaginary if the discriminant is less than zero.
How does the video determine the nature of roots for a given quadratic equation?
-The video determines the nature of roots by calculating the discriminant and then comparing it to zero and checking if it is a perfect square to categorize the roots as real and equal, rational and unequal, irrational and unequal, or no real roots (imaginary).
What is the significance of the discriminant being equal to zero?
-If the discriminant is equal to zero, it indicates that the quadratic equation has real and equal roots.
Can you provide an example from the video where the discriminant is greater than zero and a perfect square?
-Yes, in the video, the example where the discriminant is greater than zero and a perfect square is the equation "x^2 + 7x + 12 + 2 = 0". After simplifying, it becomes "x^2 + 7x + 10 = 0", and the discriminant is "7^2 - 4 * 1 * 10 = 49 - 40 = 9", which is a perfect square and greater than zero.
What does it mean if the discriminant is greater than zero but not a perfect square?
-If the discriminant is greater than zero but not a perfect square, it means the quadratic equation has irrational and unequal roots.
What is the nature of roots for a quadratic equation with a negative discriminant?
-For a quadratic equation with a negative discriminant, the nature of the roots is no real roots or imaginary.
How does the video handle a quadratic equation not in standard form?
-The video instructs to first convert the quadratic equation to standard form by combining like terms before extracting the values of a, b, and c to calculate the discriminant.
What should be noted when substituting values into the discriminant formula?
-When substituting values into the discriminant formula, it is important to ensure that the quadratic equation is in standard form and that the values of a, b, and c are correctly identified as they directly affect the discriminant calculation.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
5.0 / 5 (0 votes)