Introducción al cálculo integral | Khan Academy en Español

Summary

El guion del video explica el clásico problema matemático de calcular el área bajo una curva entre dos límites, utilizando la aproximación de rectángulos con base en delta x. Se introduce el concepto de integral definida como el límite de esta suma cuando delta x se vuelve infinitesimal y el número de rectángulos, n, tiende a infinito. La integral se relaciona con la derivada a través del teorema fundamental del cálculo, mostrando cómo la integración y la derivada están intrínsecamente conectadas, lo que revela la belleza y poder del cálculo integral.

Takeaways

• 📊 La función f(x) se representa gráficamente por una curva en el plano cartesiano.
• ⏱ Desde hace mucho tiempo, los matemáticos han buscado calcular el área bajo una curva y entre dos ejes x, denotados como 'a' y 'b'.
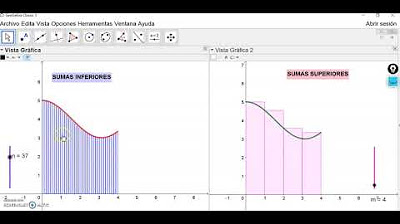
• 📐 Para aproximar el área bajo la curva, se divide el intervalo en secciones de ancho delta x, que pueden ser iguales o no.
• 📏 Se utilizan rectángulos para estimar el área, donde la altura de cada rectángulo es el valor de la función en el lado derecho de su base.
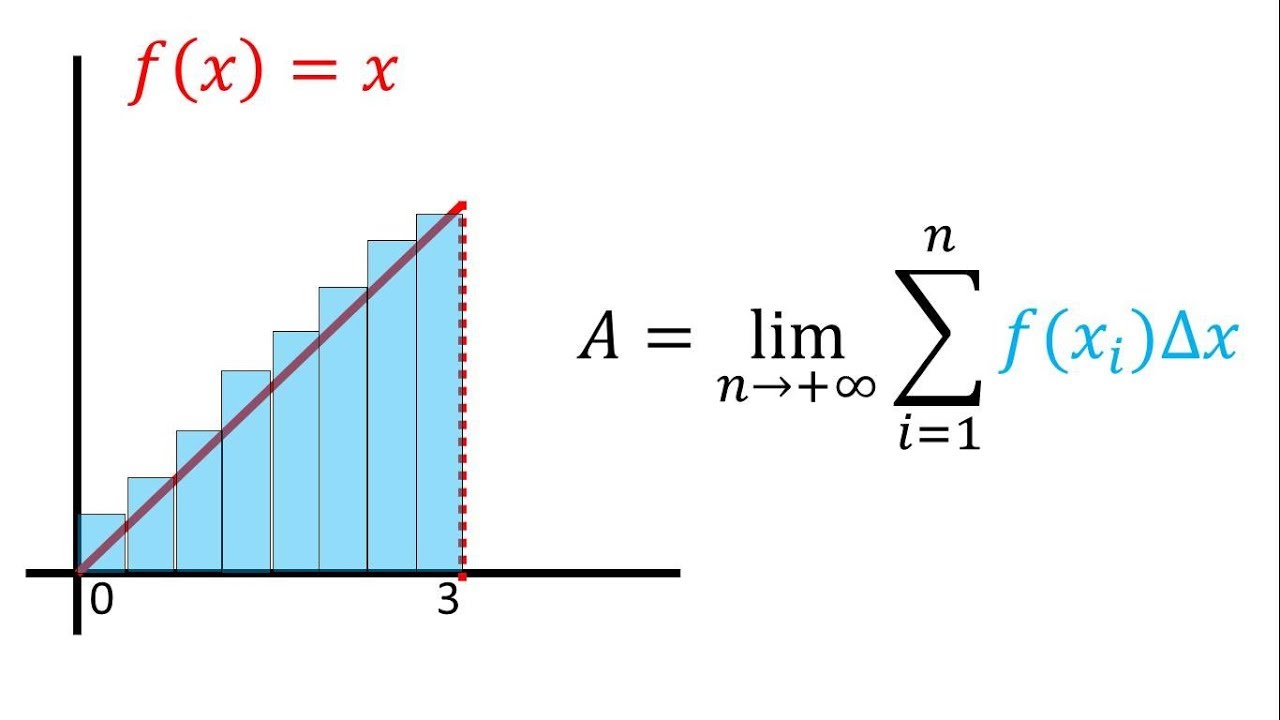
• 🔍 El área de cada rectángulo se calcula como el producto de la altura (f(x_i)) y el ancho delta x.
• 📝 La suma de las áreas de todos los rectángulos proporciona una aproximación del área total bajo la curva.
• 🔬 Al disminuir el tamaño de delta x (haciéndolo más delgado) y aumentar el número de rectángulos, la aproximación se vuelve más precisa.
• 🌐 La idea central del cálculo integral es aproximar áreas mediante la suma de un número infinito de elementos infinitesimalmente pequeños.
• 🧮 El cálculo integral se basa en el concepto de límite cuando el número de elementos (n) tiende a infinito y delta x se vuelve infinitesimalmente pequeño.
• 🔄 La integración está estrechamente relacionada con la derivación, como se verá en el teorema fundamental del cálculo, donde la integración y la antiderivación son conceptos complementarios.

Q & A

¿Qué problema clásico de matemáticas se describe en el guion?

Se describe el problema de encontrar el área bajo una curva entre dos límites, x=a y x=b.

¿Cómo se pueden mejorar las aproximaciones para encontrar el área bajo la curva?

Se pueden mejorar las aproximaciones haciendo las secciones delta x más pequeñas, es decir, aumentando el número de rectángulos.

¿Qué método se utiliza para calcular la altura de los lados de los rectángulos en la aproximación?

Se utiliza el valor de la función f(x) en el lado derecho de cada rectángulo como la altura correspondiente.

¿Qué sucede cuando delta x se vuelve infinitesimalmente pequeña y n tiende a infinito?

Cuando delta x se vuelve infinitesimalmente pequeña y n tiende a infinito, la suma de las áreas de los rectángulos se aproxima a la integral definida de la función.

¿Qué es la integral definida y cómo se relaciona con el cálculo integral?

La integral definida es una operación que suma un número infinito de elementos infinitesimalmente pequeños, y es la base del cálculo integral.

¿Cómo se representa la integral definida en notación simbólica?

La integral definida se representa con el símbolo de integral, que es similar a la suma sigma, pero para un número infinito de elementos.

¿Qué es el cálculo integral y cómo se relaciona con el cálculo diferencial?

El cálculo integral es una rama del cálculo que se relaciona con el cálculo diferencial a través del teorema fundamental del cálculo, donde la integración está relacionada con la antiderivada.

¿Qué es una antiderivada y cómo se relaciona con la derivada?

Una antiderivada es una función de la cual se puede obtener la derivada dada, es decir, es una función que, al derivarla, nos da la función original.

¿Qué es el teorema fundamental del cálculo y cómo conecta la integración con la derivada?

El teorema fundamental del cálculo conecta la integración con la derivada, estableciendo que si se conoce la derivada de una función, se puede encontrar su antiderivada o función original.

¿Cuál es la idea central detrás del cálculo integral según el guion?

La idea central del cálculo integral es la aproximación del área bajo una curva a través de la suma de un número infinito de rectángulos infinitesimalmente pequeños.