Suma de Riemann ¿Qué es? ¿De dónde sale? EXPLICACIÓN COMPLETA
Summary
TLDREl script explica la definición de una integral como una suma de rectángulos para calcular el área bajo una curva en un intervalo. Se descompone el intervalo en subintervalos y se utilizan rectángulos cuya base es delta x, calculado dividiendo el intervalo total entre el número de rectángulos (n). La altura de cada rectángulo se determina evaluando la función en un punto dentro del subintervalo. La aproximación del área se mejora al aumentar el número de rectángulos, y el área exacta se alcanza cuando n tiende a infinito, lo que se representa con la notación de Leibniz. Este concepto se extiende a integrales de múltiples variables.
Takeaways
- 📘 La definición de una integral como una suma de rectángulos se explica en el guion, para calcular el área bajo una curva y por encima del eje X en un intervalo específico.
- 📐 Se menciona que el intervalo puede dividirse en subintervalos de cualquier longitud, pero para simplificar, se asume que todos tienen la misma longitud.
- 🔢 El número de subintervalos se denota como 'n', y se calcula el ancho de cada subintervalo (delta x) dividiendo la longitud total del intervalo entre 'n'.
- 📏 Se elige un punto dentro de cada subintervalo para calcular la altura de los rectángulos, que es el valor de la función en ese punto (f(x) en x=y).
- 📋 La fórmula para el área de cada rectángulo se presenta como base (delta x) por altura (f(x) en x=y), que se escribe como 'f(x_i) * Δx'.
- 📊 Para aproximar el área bajo la curva, se suman las áreas de todos los rectángulos, lo que se denota con la notación sigma (Σ).
- 📉 El proceso de hacer los rectángulos más delgados (aumentando el número 'n') se describe para acercarse al área exacta debajo de la curva.
- 📌 Se introduce el concepto de límites para definir la integral definida, donde el número de rectángulos tiende a ser infinito y el ancho de los rectángulos tiende a cero.
- 📈 La integral definida se representa con la notación de Leibniz, que incluye los límites de integración, la función a integrar y el diferencial.
- 📚 Se menciona que estas ideas se utilizarán para definir integrales de dos variables, sugiriendo una extensión del concepto de integrales unidimensionales.
Q & A
¿Qué es una integral y cómo se relaciona con el cálculo de áreas?
-Una integral es una suma de rectángulos que aproxima el área debajo de una curva y encima del eje x en un intervalo determinado. Se utiliza para calcular áreas, volumes, y otras cantidades que varían continuamente.
¿Cómo se divide el intervalo ab para calcular una integral?
-El intervalo ab se divide en varios subintervalos más pequeños, que pueden tener longitudes diferentes. Para simplificar, se asume a menudo que tienen la misma longitud, llamada delta x.
¿Qué es delta x y cómo se calcula?
-Delta x es la longitud de base de los rectángulos que se utilizan para aproximar el área debajo de la curva. Se calcula dividiendo la distancia total del intervalo (b - a) entre el número de rectángulos n.
¿Cómo se elige el punto dentro de un rectángulo para calcular su altura?
-Se elige un punto dentro del rectángulo, generalmente en la intersección con la gráfica de la función, y se utiliza para calcular la altura del rectángulo evaluando la función en ese punto.
¿Qué representa la altura de un rectángulo en el contexto de una integral?
-La altura de un rectángulo en una integral representa el valor de la función evaluada en el punto x y, que indica cuánto se eleva el rectángulo sobre el eje x.
¿Cómo se calcula el área de un rectángulo en el proceso de integración?
-El área de un rectángulo en el proceso de integración se calcula multiplicando la base (delta x) por la altura (valor de la función en el punto x y).
¿Qué simboliza la notación sigma en el cálculo de integrales?
-La notación sigma (Σ) representa la suma de una serie de términos, donde i varía de 1 a n, y se utiliza para sumar el área de todos los rectángulos en el proceso de integración.
¿Qué sucede con los rectángulos cuando n tiende a infinito?
-Cuando n tiende a infinito, los rectángulos se vuelven más delgados y su número aumenta indefinidamente, lo que hace que su área se aproxime más al área exacta debajo de la curva.
¿Qué es la integral definida y cómo se relaciona con los límites?
-La integral definida es el límite que se toma cuando el número de rectángulos n tiende a infinito, y representa el área exacta debajo de la curva en el intervalo considerado. Los límites son fundamentales en el cálculo para definir conceptos como la derivada, la integral y las series.
¿Cómo se representa gráficamente una integral definida?
-Una integral definida se representa gráficamente con una s alargada, conocida como la notación de Leibniz, que indica los límites de la integral (a y b), la función a integrar y el diferencial que indica la variable de integración.
¿Cómo se extienden los conceptos de integrales de una variable a funciones de más variables?
-Los conceptos de integrales de una variable se extienden a funciones de más variables mediante sumas de rectángulos en múltiples dimensiones, lo que permite calcular áreas, volúmenes y otras medidas en espacios más complejos.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Reescribir una integral definida como el límite de una suma de Riemann | Khan Academy en Español

Sumatorias

Cálculo Integral 01:Área bajo una curva. Area under a curve
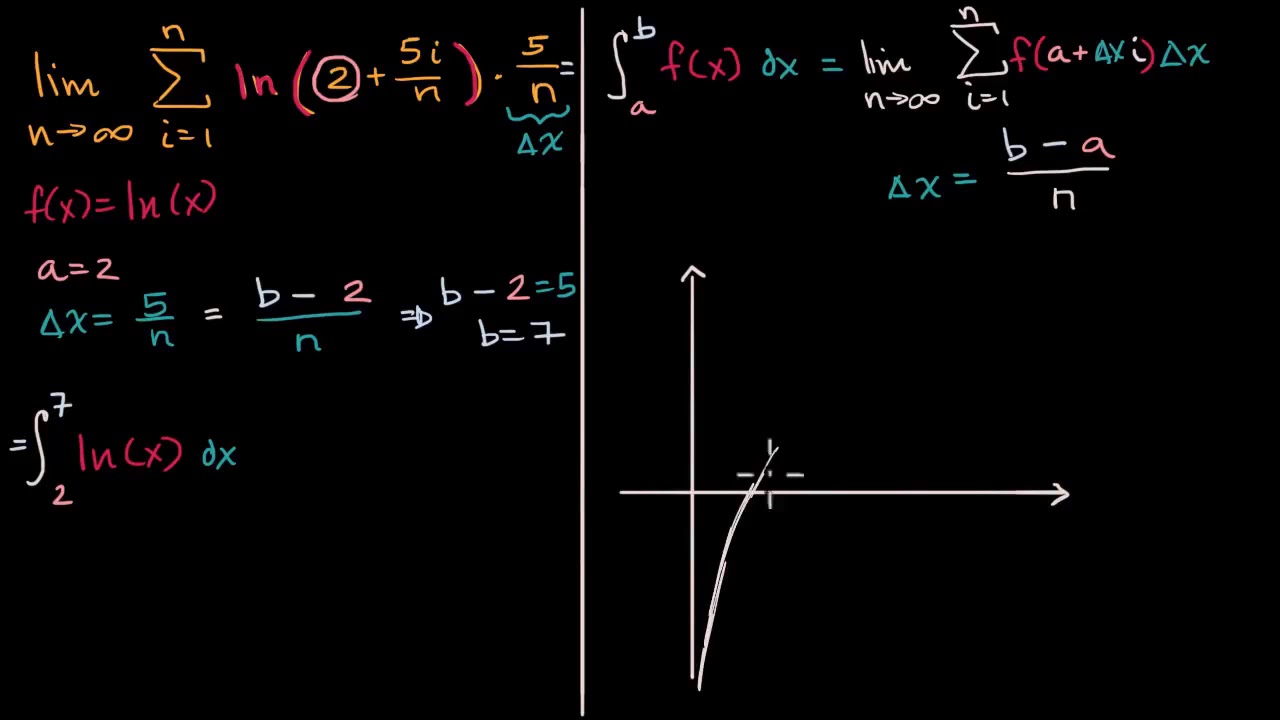
Escribir el límite de una suma de Riemann como una integral definida | Khan Academy en Español

Área bajo la curva (Cálculo integral) Método de rectángulos. EJEMPLO 1

Área bajo la curva por Extremos Derechos
5.0 / 5 (0 votes)
