La pendiente | ¿Qué es una función lineal? | y=mx+b| funciones
Summary
TLDREl guión ofrece una explicación detallada sobre la función lineal, enfocándose en la pendiente, representada por 'm'. Se describe cómo la pendiente indica si la función es creciente, decreciente o constante. Se ilustra con ejemplos cómo calcular la pendiente usando la fórmula (x2 - x1) / (y2 - y1) y se discute su importancia en el comportamiento de la función. El guión invita a los estudiantes a participar en los comentarios para resolver dudas y profundizar en el tema.
Takeaways
- 📚 La función lineal es una de las más importantes en matemáticas y se representa con la ecuación f(x) = m*x + b.
- 📈 La pendiente 'm' de una función lineal indica la inclinación de la recta y es crucial para entender su comportamiento.
- ⬆️ Si la pendiente 'm' es positiva, la función es creciente, lo que significa que aumenta a medida que avanza en el eje x.
- ➡️ Si la pendiente 'm' es cero, la función es constante, no cambia a lo largo del eje x.
- ⬇️ Si la pendiente 'm' es negativa, la función es decreciente, lo que significa que disminuye a medida que avanza en el eje x.
- 🔢 La fórmula para calcular la pendiente dada dos puntos es m = (y2 - y1) / (x2 - x1), donde (x1, y1) y (x2, y2) son los puntos dados.
- 📉 La pendiente positiva sugiere una función que 'sube', como si un señor estuviera subiendo una cuesta.
- 📊 La pendiente negativa sugiere una función que 'baja', como si el señor estuviera descendiendo.
- 🔍 La pendiente cero indica una función que es 'plana', es decir, no cambia su valor a lo largo del eje x.
- 📐 La pendiente es una herramienta útil para entender y visualizar cómo se desplaza una función lineal en el plano cartesiano.
- 👨🏫 El script ofrece una revisión y explicación detallada de la pendiente, invitando a los estudiantes a practicar y resolver problemas relacionados con ella.
Q & A
¿Qué es una función lineal y cómo se representa?
-Una función lineal es una relación entre dos variables que sigue una línea recta en un gráfico. Se representa con la ecuación y = mx + b, donde 'y' es la variable dependiente, 'x' es la variable independiente, 'm' es la pendiente de la línea y 'b' es el ordenamiento de la línea.
¿Qué representa la letra 'm' en la ecuación de una función lineal?
-La letra 'm' representa la pendiente de la función lineal, que es la inclinación de la línea en el gráfico.
¿Qué significa si la pendiente 'm' es mayor a 0?
-Si la pendiente 'm' es mayor a 0, significa que la función es creciente, es decir, la línea en el gráfico se inclina hacia arriba a medida que aumenta el valor de 'x'.
¿Qué ocurre si la pendiente 'm' es igual a 0?
-Si la pendiente 'm' es igual a 0, la función no es creciente ni decreciente, sino que es constante, lo que significa que la línea es horizontal en el gráfico.
¿Qué indica una pendiente 'm' menor que cero?
-Una pendiente 'm' menor que cero indica que la función es decreciente, es decir, la línea en el gráfico se inclina hacia abajo a medida que aumenta el valor de 'x'.
¿Cómo se calcula la pendiente de una función lineal dada dos pares ordenados?
-La pendiente se calcula utilizando la fórmula m = (y2 - y1) / (x2 - x1), donde (x1, y1) y (x2, y2) son los dos pares ordenados dados.
¿Cómo se interpreta la pendiente positiva en términos de movimiento en el gráfico?
-Una pendiente positiva indica que a medida que aumenta el valor de 'x', el valor de 'y' también aumenta, lo que se visualiza como un movimiento hacia arriba en el gráfico.
¿Qué se entiende por 'cuesta' en el contexto de la función lineal creciente?
-Una 'cuesta' es una metáfora para describir una función lineal creciente, donde la línea se inclina hacia arriba, similar a cómo una cuesta se eleva hacia arriba.
¿Cómo se interpreta la pendiente negativa en términos de movimiento en el gráfico?
-Una pendiente negativa indica que a medida que aumenta el valor de 'x', el valor de 'y' disminuye, lo que se visualiza como un movimiento hacia abajo en el gráfico.
¿Qué se puede deducir de una función lineal cuando la pendiente es cero y el ordenamiento 'b' es distinto de cero?
-Cuando la pendiente es cero y el ordenamiento 'b' es distinto de cero, la función lineal es constante y la línea es horizontal en el gráfico, pero no pasa por el origen, sino que se desplaza verticalmente según el valor de 'b'.
¿Qué es el ordenamiento 'b' en la ecuación de una función lineal y qué representa?
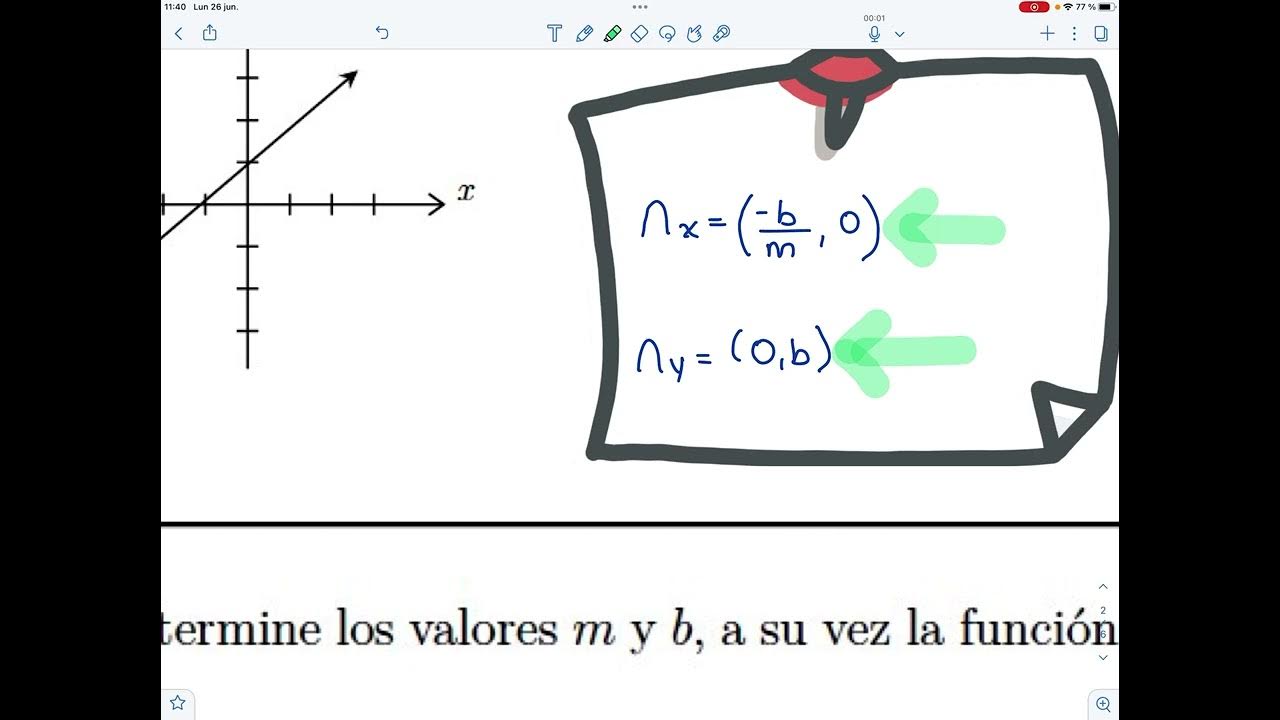
-El ordenamiento 'b' en la ecuación de una función lineal es la intersección de la línea con el eje y, representando el punto en el que la línea corta el eje y en el caso de que la pendiente sea cero.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenant5.0 / 5 (0 votes)