A Problem with the Parallel Postulate - Numberphile
Summary
TLDRThis script delves into the parallel postulate of Euclidean geometry, originally from Euclid's Elements, and its implications in different geometrical models. It explains the postulate's traditional interpretation in plane geometry, where through a point not on a given line, there's exactly one non-intersecting line. The script then contrasts this with spherical geometry, where no parallel lines exist, and hyperbolic geometry, where multiple parallel lines are possible. The discussion highlights the postulate's uniqueness and the diversity of geometrical systems, challenging the idea that it's a necessary consequence of Euclid's first four postulates.
Takeaways
- 📚 The parallel postulate is a fundamental concept in Euclidean geometry, first introduced in Euclid's Elements around 300 BC.
- 🔍 The postulate states that for a given line and a point not on the line, there is exactly one line through the point that does not intersect the original line, emphasizing uniqueness.
- 🤔 The parallel postulate was historically considered a prime example of deductive reasoning, where truths are derived from a set of axioms.
- 🌐 The script discusses the limitations of the parallel postulate by introducing non-Euclidean geometries, such as spherical geometry, where the postulate does not hold.
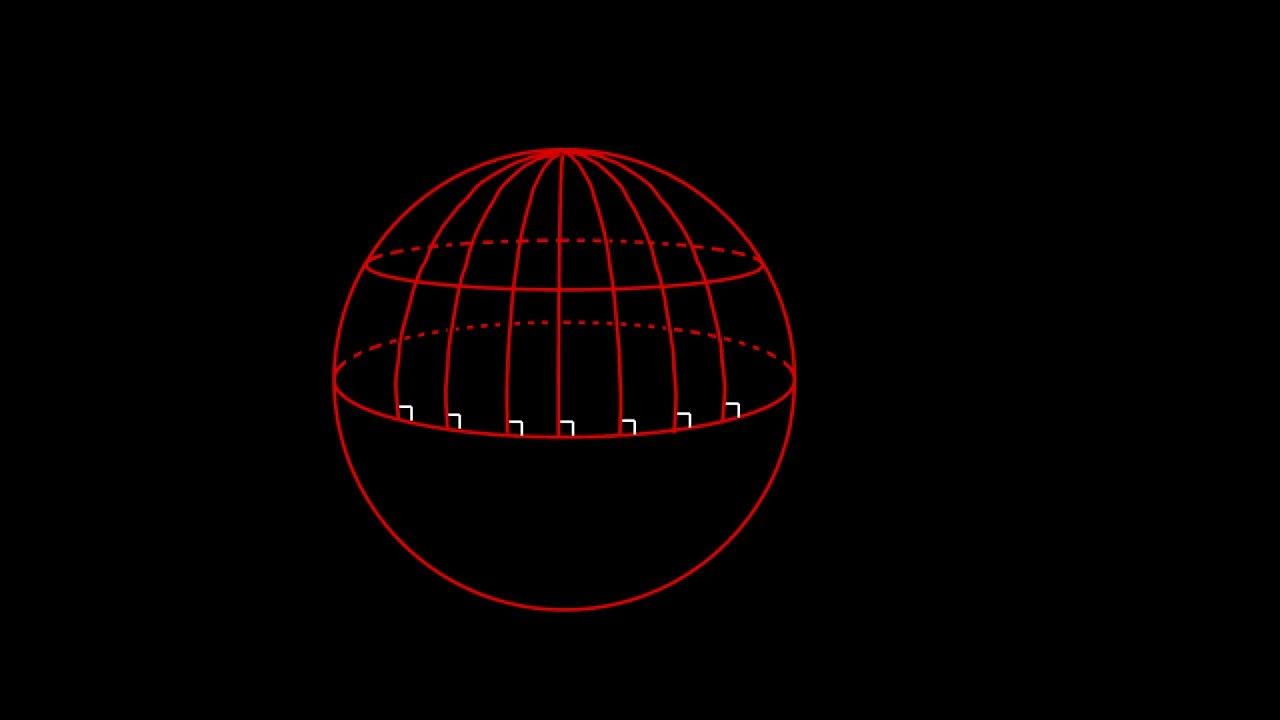
- 🌍 In spherical geometry, represented by a 2D surface on a sphere, there are no parallel lines because any line (great circle) through a point not on a given line will intersect it.
- 📏 The concept of a 'line' in spherical geometry differs from the Euclidean plane, with 'lines' being great circles or segments of great circles.
- 🛑 The failure of the parallel postulate in spherical geometry indicates that it is not a necessary consequence of the first four postulates of Euclid.
- 🔄 The script also introduces hyperbolic geometry, another non-Euclidean geometry where there are infinitely many parallel lines to a given line through a point not on it.
- 📊 In hyperbolic geometry, lines are defined differently, either as straight lines through the center of the model or as segments of circles orthogonal to the boundary.
- 🧩 The existence of non-Euclidean geometries shows that there are multiple ways to approach two-dimensional geometry, challenging the uniqueness of the Euclidean model.
- 💭 The script suggests that Euclid might have been aware of the peculiar nature of the parallel postulate, as it was not used in his work until later sections.
Q & A
What is the parallel postulate?
-The parallel postulate is a statement in Euclidean geometry that asserts that through a point not on a given line, there is exactly one line parallel to the given line. It was originally presented by Euclid in his 'Elements' around 300 BC.
Why was the parallel postulate significant in the 19th century?
-In the 19th century, the parallel postulate was considered an example of what it means to know something. It was highly valued because it represented the deductive nature of geometry, where truths are derived from a set of axioms.
What is the difference between a line and a line segment in the context of the parallel postulate?
-In the context of the parallel postulate, a line is an infinite straight path that extends indefinitely in both directions, while a line segment is a part of a line that is bounded by two distinct end points and has a finite length.
How is the parallel postulate stated in Euclid's 'Elements'?
-In Euclid's 'Elements', the parallel postulate is stated in terms of angles. If a line and a point not on the line create two angles that sum to less than 180 degrees, the lines, when extended to infinity, will intersect.
What is a model of geometry where the parallel postulate does not hold?
-A model of geometry where the parallel postulate does not hold is spherical geometry, where the surface is a sphere, and lines are represented by great circles, such as the equator or lines of longitude.
What is a great circle in spherical geometry?
-A great circle in spherical geometry is the largest circle that can be drawn on the surface of a sphere. It is the intersection of the sphere with a plane that passes through the center of the sphere.
How does the concept of distance differ between Euclidean and spherical geometry?
-In Euclidean geometry, distance is measured using a straight line between two points, following the Pythagorean theorem. In spherical geometry, distance is measured along the shortest path on the sphere's surface, which is along a great circle.
What is hyperbolic geometry and how does it relate to the parallel postulate?
-Hyperbolic geometry is a non-Euclidean geometry where the parallel postulate is replaced by the existence of more than one line through a point parallel to a given line. In this geometry, lines are represented by segments of circles orthogonal to the boundary of a disk.
Why was there an upheaval in geometry in the 19th century regarding the parallel postulate?
-The upheaval in geometry in the 19th century occurred because mathematicians discovered that the first four postulates of Euclid could be used in other geometries, such as spherical and hyperbolic geometry, without the fifth postulate, showing that it was not a necessary consequence of the others.
What does the failure of the parallel postulate in spherical and hyperbolic geometries imply about the nature of geometry?
-The failure of the parallel postulate in spherical and hyperbolic geometries implies that there are multiple consistent ways to do geometry in two dimensions, each with its own set of rules and properties, challenging the idea of a single, universal geometry.
How did the understanding of the parallel postulate evolve over time?
-Initially, the parallel postulate was accepted as a fundamental truth in Euclidean geometry. However, with the development of non-Euclidean geometries in the 19th century, it became clear that the postulate was not universally true and was instead a specific case within a broader spectrum of geometric possibilities.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

The History of Non-Euclidean Geometry - The Great Quest - Part 2 - Extra History

Los Universos Paralelos Ocultos Vienen de Hace Muchos Años...
Classroom Aid - Non-Euclidean Geometry

The History of Non-Euclidean Geometry - Sacred Geometry - Part 1 - Extra History

General Relativity: The Curvature of Spacetime

Non-Euclidean Geometry [Topics in the History of Mathematics]
5.0 / 5 (0 votes)
