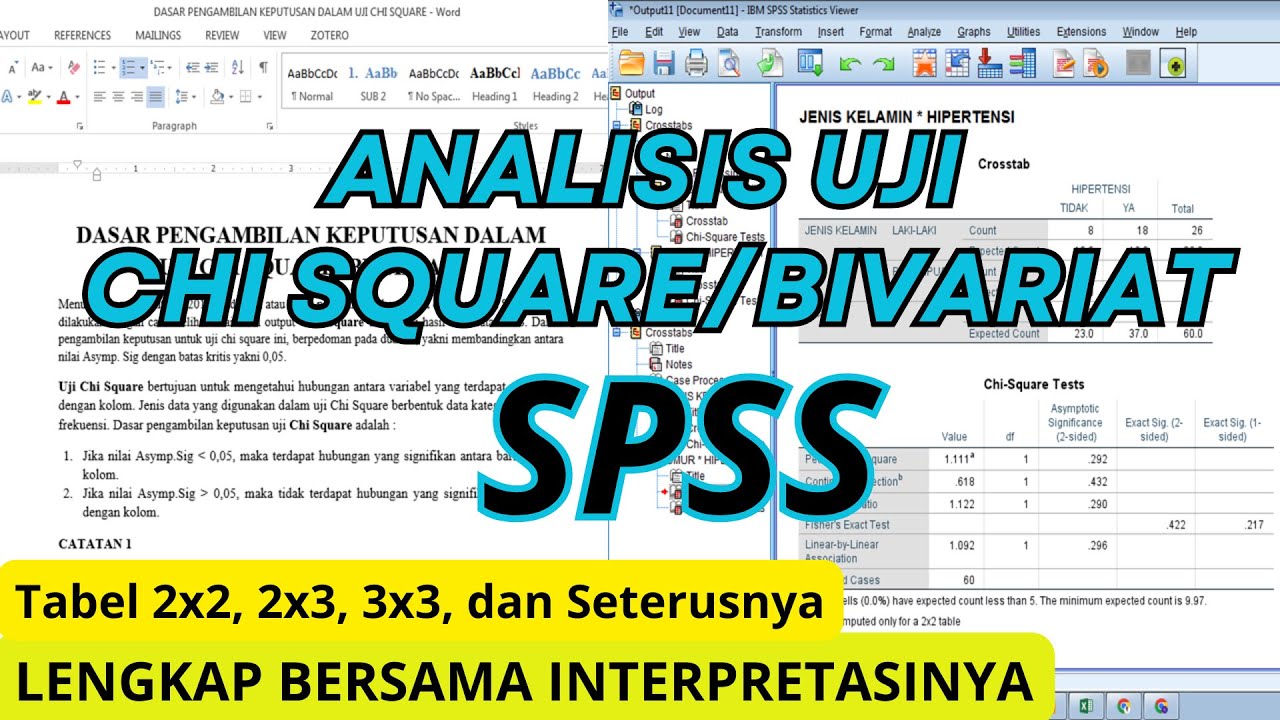
How to calculate a Chi-Square Test?

Summary

This video explains how to perform a chi-square test to determine if there's a relationship between two categorical variables, in this case, gender and preferred newspaper. It walks through the process using a survey, creating a contingency table, and calculating the chi-square value with both statistical software and by hand. The test compares observed frequencies to expected frequencies, and the results show that there's no significant relationship between gender and the preferred newspaper. A critical chi-square value is also discussed to determine whether to accept or reject the null hypothesis.

Takeaways

• 😀 The Chi-Square test is used to determine if there is a relationship between two categorical variables.
• 😀 The null hypothesis in a Chi-Square test assumes that there is no relationship between the variables being tested.
• 😀 The alternative hypothesis suggests that there is a relationship between the two variables.
• 😀 Data is collected via a survey or questionnaire, and the results are displayed in a contingency table.
• 😀 A Chi-Square test can be calculated using statistical software like Data Tab or manually by hand.
• 😀 In the example, the Chi-Square test is used to explore whether gender influences preferred newspaper choice.
• 😀 The contingency table is used to compare the observed frequencies with the expected frequencies assuming independence.
• 😀 A Chi-Square test compares the observed data with what would be expected if the variables were independent.
• 😀 The P-value resulting from the Chi-Square test helps to decide whether to reject the null hypothesis. A P-value greater than 0.05 means the null hypothesis is not rejected.
• 😀 When calculating the Chi-Square by hand, the formula involves summing the squared differences between observed and expected values, divided by expected values.
• 😀 To determine the critical Chi-Square value, you need the degrees of freedom, which are calculated by multiplying the number of rows minus one and the number of columns minus one.

Q & A

What is the main purpose of a Chi-Square test?

The Chi-Square test is used to determine if there is a relationship between two categorical variables, such as gender and preferred newspaper in this example.

What are the null and alternative hypotheses in the Chi-Square test example?

The null hypothesis states that there is no relationship between gender and preferred newspaper, while the alternative hypothesis suggests there is a relationship between the two variables.

What kind of data is used for a Chi-Square test?

A Chi-Square test is applied to categorical data, which is divided into categories such as gender (male, female) and preferred newspaper (e.g., New York Post, USA Today).

How are the results of a survey displayed for a Chi-Square test?

The results are displayed in a contingency table showing the frequency of combinations between the variables, such as how many males prefer New York Post or how many females prefer USA Today.

What is the significance of the P-value in a Chi-Square test?

The P-value helps determine whether the result is statistically significant. If the P-value is smaller than the significance level (usually 0.05), the null hypothesis is rejected, indicating a relationship between the variables.

What does the contingency table show in the Chi-Square test example?

The contingency table shows the observed frequencies of combinations between gender and preferred newspaper. For instance, it shows how many males and females prefer different newspapers like the New York Post or USA Today.

How is the Chi-Square statistic calculated by hand?

The Chi-Square statistic is calculated using the formula: χ² = Σ[(O_k - E_k)² / E_k], where O_k is the observed frequency and E_k is the expected frequency for each cell in the contingency table.

What does the Chi-Square test compare to determine the significance of the variables?

The Chi-Square test compares the observed frequencies in the contingency table with the expected frequencies assuming the variables are independent. The difference between these values determines the Chi-Square statistic.

What is the critical Chi-Square value, and how is it used?

The critical Chi-Square value is the threshold used to determine whether to reject the null hypothesis. It is obtained from a Chi-Square table, using the degrees of freedom and the chosen significance level (usually 0.05).

How are degrees of freedom calculated for a Chi-Square test?

Degrees of freedom are calculated as the product of the number of rows minus one and the number of columns minus one in the contingency table. For example, if there are 4 rows and 2 columns, the degrees of freedom would be (4-1) * (2-1) = 3.

What conclusion is drawn when the calculated Chi-Square value is less than the critical value?

If the calculated Chi-Square value is less than the critical value, the null hypothesis is not rejected, meaning there is no significant relationship between the two variables, such as gender and preferred newspaper.