Ecuación de la parábola con vértice en el origen y directriz y=-10
Summary
TLDREste video explica el proceso para determinar la ecuación de una parábola en función de su directriz y su foco. Se muestra cómo calcular el valor de *p* a partir de la directriz dada, y cómo esto afecta la forma y orientación de la parábola. A través de ejemplos, el video detalla cómo llegar a la ecuación estándar de una parábola vertical que abre hacia arriba o hacia abajo, y la relación entre la ecuación algebraica y la representación geométrica. El análisis culmina con una validación de los resultados obtenidos desde un enfoque tanto algebraico como geométrico.
Takeaways
- 😀 Se está analizando el caso de una parábola con vértices en el origen y la directriz proporcionada.
- 😀 En el caso número 2, se compara una parábola vertical con la ecuación de la directriz dada.
- 😀 La ecuación de la directriz en el caso 2 es y = -10, lo que corresponde a un valor de p negativo.
- 😀 Para determinar el valor de p, se utiliza la ecuación de la directriz, donde se despeja el valor de p.
- 😀 El valor de p se obtiene al aplicar el signo negativo, lo que da como resultado un valor positivo para p.
- 😀 Con el valor de p, se puede calcular la ecuación de la parábola, que será de la forma x² = 4p * y.
- 😀 En este caso, con p = 10, la ecuación de la parábola es x² = 40y.
- 😀 La parábola es vertical porque el cuadrado está sobre la x, lo que implica que abre hacia arriba o hacia abajo dependiendo del signo de p.
- 😀 La directriz, que es y = -10, se ubica en el eje y en la posición -10, lo que verifica la relación geométrica con el foco.
- 😀 El análisis geométrico y analítico confirma que la directriz está en sentido opuesto al foco, lo que valida los resultados obtenidos.
Q & A
¿Cuál es el objetivo principal de este ejercicio?
-El objetivo principal es determinar la ecuación de la parábola dada la información sobre la directriz y el foco, analizando casos de parábolas horizontales y verticales.
¿Cómo se identifica el tipo de parábola en este ejercicio?
-El tipo de parábola se identifica observando la orientación de su ecuación. Si la ecuación es de la forma x² = 4p·y, la parábola es vertical, y si es de la forma y² = 4p·x, la parábola es horizontal.
¿Qué información se utiliza para determinar la ecuación de la parábola en el caso 1?
-En el caso 1, se utiliza la ecuación de la directriz, que está dada por x = -p, y se despeja el valor de p para poder escribir la ecuación de la parábola.
¿Cuál es la ecuación general para una parábola vertical?
-La ecuación general de una parábola vertical es x² = 4p·y, donde p es la distancia del vértice al foco o la directriz.
¿Qué pasa cuando el valor de p es positivo en la parábola vertical?
-Cuando el valor de p es positivo, la parábola abre hacia arriba, ya que la ecuación de la parábola es positiva en el término de la y.
¿Cómo se obtiene la ecuación de la parábola en el caso 2?
-En el caso 2, se utiliza el valor de p, que se obtiene de la ecuación de la directriz. Al resolver la ecuación, se obtiene la forma de la ecuación de la parábola como x² = 40y.
¿Cómo se interpreta geométricamente la directriz y el foco?
-Geométricamente, la directriz es una línea que está en dirección opuesta al foco. Los puntos de la parábola son equidistantes de la directriz y el foco.
¿Cómo se relacionan la ecuación analítica y la geométrica en el ejercicio?
-La ecuación analítica de la parábola coincide con la interpretación geométrica, ya que ambas describen la misma figura, donde los puntos son equidistantes del foco y la directriz.
¿Qué significa el valor negativo de la directriz en este ejercicio?
-El valor negativo de la directriz indica que la directriz está en el lado opuesto al foco, lo que afecta la orientación de la parábola.
¿Cómo se verifica que los resultados obtenidos en la ecuación de la parábola son correctos?
-Se verifica que los resultados sean correctos comprobando que la ecuación de la parábola cumple con las condiciones geométricas, como la relación entre el vértice, el foco y la directriz.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Ex 2: Conic Section: Parabola with Vertical Axis and Vertex NOT at the Origin (Down)

Elementos de una parábola dada ecuación │ origen

Shifted Conics | Parabolas where the Vertex is not the Origin, Finding Focus and Directrix
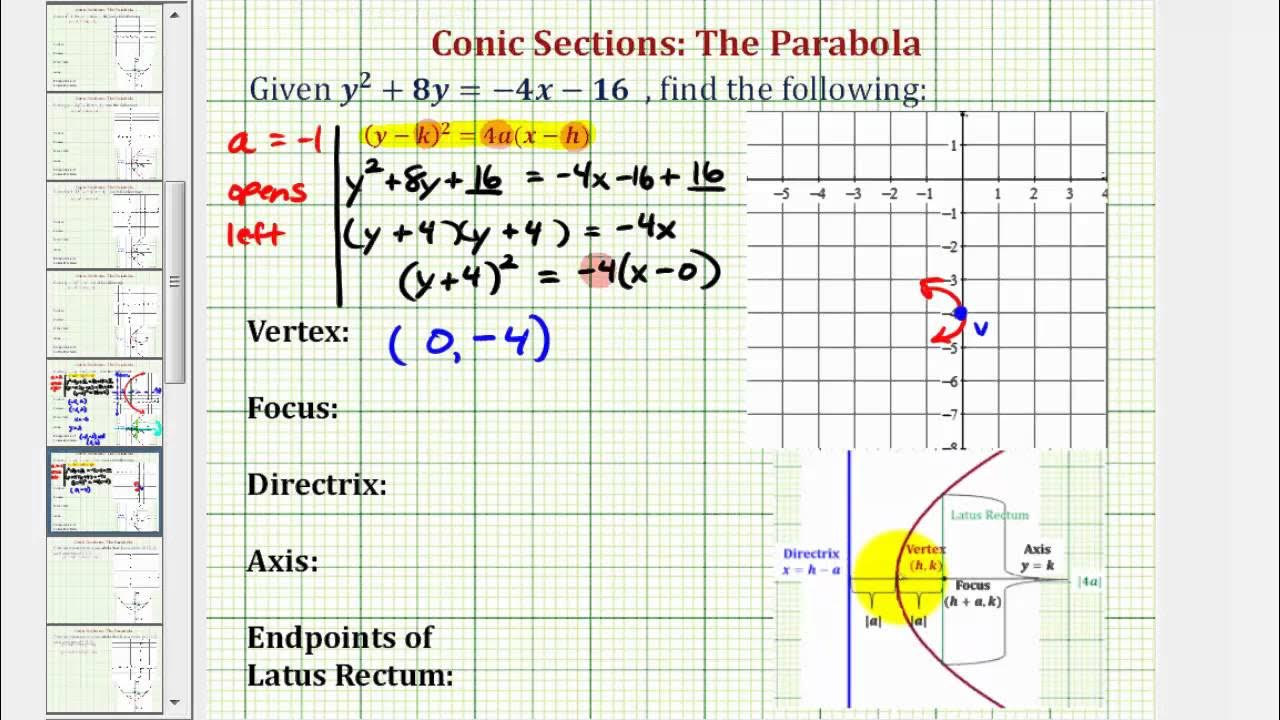
Ex 10: Conic Section: Parabola with Horizontal Axis and Requires Completing the Square (Left)

🧲 PARÁBOLA: Concepto y elementos (foco, vértice, L.R, directriz, distancia focal) | Juliana la profe

Exercise 1 Parabola
5.0 / 5 (0 votes)