Rotation Matrix Parametrization
Summary
TLDREste video aborda la parametrización de matrices de rotación, un tema fundamental en cinemática robótica. El Dr. Rico explora diferentes enfoques como los ángulos de Euler, los ángulos de rotación roll-pitch-yaw, y la parametrización de eje-ángulo. Además, explica el teorema de Euler, las soluciones inversas para calcular los ángulos de Euler a partir de una matriz de rotación y cómo aplicar la fórmula de Rodríguez para obtener la matriz de rotación correspondiente a un eje y un ángulo. También se mencionan las cuaterniones y se recomienda estudiar los apéndices del capítulo para profundizar en temas avanzados como la cinemática inversa.
Takeaways
- 😀 El teorema de rotación de Euler establece que cualquier matriz de rotación en el grupo ortogonal especial 3 se puede describir con tres parámetros.
- 😀 Las matrices de rotación tienen 9 entradas, pero deben cumplir restricciones: cada columna tiene longitud unitaria y las columnas son ortogonales, lo que reduce la libertad de grados a 3.
- 😀 Los ángulos de Euler son una forma común de representar rotaciones, utilizando tres ángulos que corresponden a rotaciones sucesivas sobre los ejes Z, Y, y Z.
- 😀 En la representación de ángulos de Euler, la rotación se realiza en tres pasos: primero sobre el eje Z, luego sobre el eje Y y finalmente sobre el eje Z nuevamente.
- 😀 El problema de la cinemática inversa para ángulos de Euler implica calcular los ángulos dados una matriz de rotación, lo cual es un problema no lineal.
- 😀 El cálculo de los ángulos de Euler es sensible a valores extremos de la matriz de rotación, como cuando el valor de r33 es igual a +1 o -1, lo que lleva a soluciones infinitas o no únicas.
- 😀 La representación de rotaciones también puede hacerse usando los ángulos de rotación de rollo, cabeceo y guiñada, comunes en aeronaves y vehículos.
- 😀 El método de los ángulos de rotación Roll-Pitch-Yaw usa un marco de referencia fijo para rotar sobre los ejes X, Y y Z.
- 😀 El ángulo de rotación y el eje de rotación se pueden obtener utilizando la fórmula de Rodrigues, que está basada en matrices skew-simétricas.
- 😀 La fórmula de Rodrigues para una rotación alrededor de un eje unitario y un ángulo theta se calcula con una matriz que depende de la matriz identidad, seno y coseno del ángulo, y el operador de skew-simetría.
- 😀 Cuando el rastro de la matriz de rotación (trace) está entre -1 y 3, existe una solución única para el ángulo de rotación y el eje; sin embargo, cuando el rastro es igual a -1, existen dos soluciones posibles para el ángulo de rotación.
Q & A
¿Qué son las matrices ortogonales especiales y qué características tienen?
-Las matrices ortogonales especiales son matrices de rotación que tienen la propiedad de que sus columnas son vectores unitarios y perpendiculares entre sí. Estas matrices pertenecen al grupo especial ortogonal SO(3), que describe las rotaciones en el espacio tridimensional. Son fundamentales en la representación de la rotación de objetos en 3D.
¿Cuál es la dimensión del grupo de matrices ortogonales especiales SO(3) y por qué?
-El grupo SO(3) tiene 3 grados de libertad. Aunque una matriz de rotación tiene 9 elementos, existen 6 restricciones debido a las condiciones de ortogonalidad (columnas perpendiculares) y normalización (longitud unitaria). Esto reduce el número de grados de libertad a 3.
¿Cómo se representa una rotación en 3D utilizando ángulos de Euler?
-La rotación en 3D se puede representar mediante tres ángulos de Euler: alfa (α), beta (β) y gamma (γ). Estos ángulos corresponden a rotaciones sucesivas sobre los ejes Z, Y y Z, respectivamente, en un sistema de coordenadas fijo o cuerpo rígido.
¿Qué sucede cuando el valor de R33 en una matriz de rotación es igual a 1 o -1?
-Cuando R33 es igual a 1 o -1, la matriz de rotación tiene soluciones infinitas para los ángulos de Euler. Esto es un caso problemático porque genera una falta de unicidad en la representación de la rotación.
¿Qué es el problema de cinemática inversa en el contexto de las matrices de rotación?
-El problema de cinemática inversa consiste en calcular los ángulos de Euler (o de otro tipo) que corresponden a una matriz de rotación dada. Esto implica resolver un sistema no lineal de ecuaciones para obtener los valores de los ángulos a partir de la matriz de rotación.
¿Qué son los ángulos de roll, pitch y yaw, y cómo se aplican en aeronáutica?
-Los ángulos de roll, pitch y yaw son convenciones utilizadas para describir la orientación de un vehículo, como un avión. Roll (alfa) describe la rotación alrededor del eje X, pitch (beta) alrededor del eje Y, y yaw (gamma) alrededor del eje Z. Estas convenciones son especialmente útiles en aeronáutica.
¿En qué consiste la parametrización de ángulo-axial y cómo se representa?
-La parametrización de ángulo-axial describe una rotación alrededor de un eje específico. El ángulo de rotación y el eje de rotación (un vector unitario) determinan completamente la rotación. Se utiliza la fórmula de Rodríguez para calcular la matriz de rotación correspondiente.
¿Qué es la fórmula de Rodríguez y para qué se utiliza?
-La fórmula de Rodríguez se utiliza para calcular una matriz de rotación dada un eje de rotación unitario y un ángulo. Esta fórmula combina la matriz identidad, el producto cruzado (usando la matriz antisimétrica) y los senos y cosenos del ángulo de rotación para construir la matriz de rotación.
¿Cuál es la relación entre los ángulos de Euler y las matrices de rotación en un sistema de referencia cuerpo fijo?
-En un sistema de referencia cuerpo fijo, los ángulos de Euler representan rotaciones sucesivas alrededor de los ejes Z, Y y Z del sistema de coordenadas. Debido a que las rotaciones son sucesivas, los ejes de rotación cambian en cada paso, lo que hace que las matrices de rotación sean producto de transformaciones no conmutativas.
¿Qué dificultades surgen cuando el valor del rastro (trace) de una matriz de rotación es igual a 3 o -1?
-Cuando el trazo de la matriz de rotación es igual a 3 o -1, el problema de cinemática inversa puede tener múltiples soluciones. Si el trazo es 3, la rotación es la identidad (sin rotación). Si el trazo es -1, la rotación es de 180 grados, lo que genera dos posibles ejes de rotación opuestos.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Introducción a la Robótica | Grados De Libertad | Cinemática Directa e Inversa

PLANEACIÓN DE TRAYECTORIAS (Introducción) | zDynamics
Robótica: Cinemática del Robot #1

1. Fundamentos de Robótica. Introducción

Transformaciones lineales en tres dimensiones | Esencia del álgebra lineal, capítulo 4b

Vectores propios y valores propios | Esencia del álgebra lineal, capítulo 10
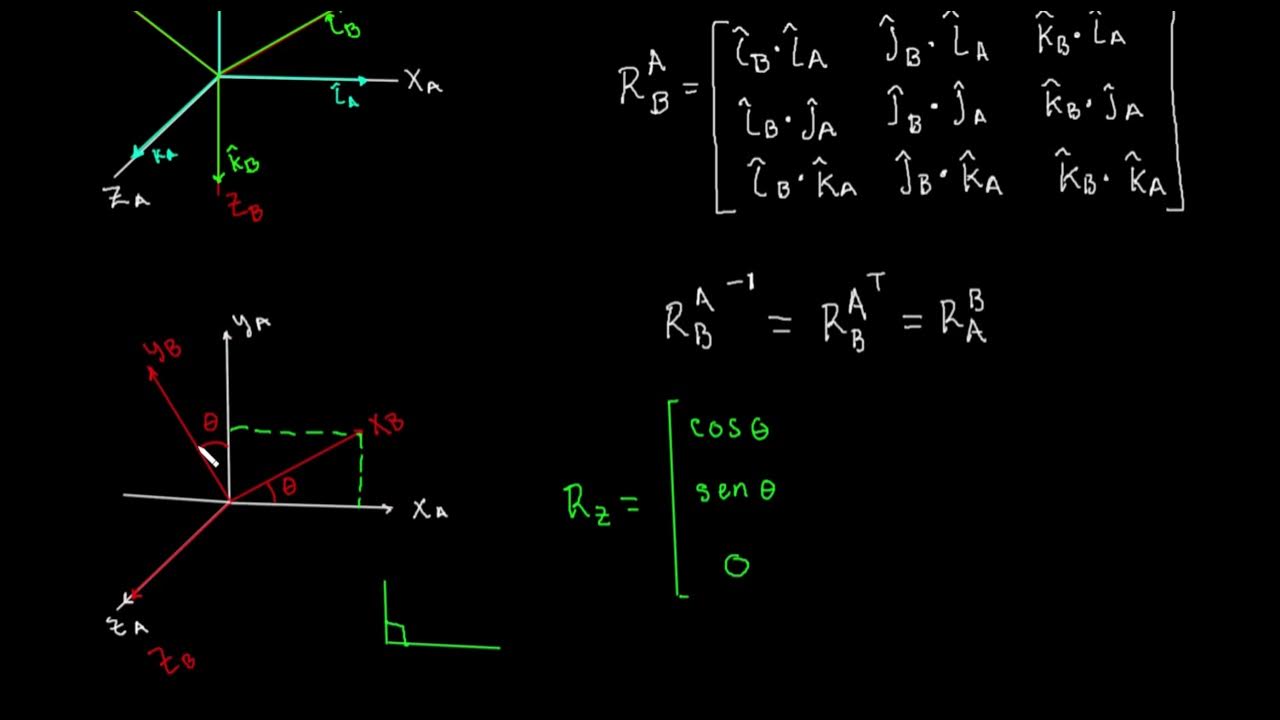
Matrices de rotación en 3D de x, y, z
5.0 / 5 (0 votes)