Radios del modelo de Bohr. Deducción utilizando física

KhanAcademyEspañol

3 Aug 201510:40

Summary

TLDREn este video, se explica el modelo de Bohr para el átomo de hidrógeno, abordando conceptos como el protón en el núcleo, la órbita del electrón y la fuerza centrípeta que lo mantiene en movimiento. Se describe cómo se calcula el radio de la órbita utilizando la ley de Coulomb y la ley de Newton, con la incorporación del momento angular cuantizado por Bohr. El video profundiza en cómo Bohr determinó que solo ciertos radios son permitidos en este modelo, destacando la importancia de la constante de Planck y el cálculo del radio fundamental en el átomo de hidrógeno.

Takeaways

😀 El modelo de Bohr para el átomo de hidrógeno describe a un electrón orbitando un núcleo con un protón, similar a los planetas alrededor del sol.
😀 Aunque el modelo de Bohr no refleja completamente la realidad, es útil para conceptos básicos y cálculos como el radio de la órbita del electrón.
😀 El electrón siente una fuerza centrípeta, atraído hacia el núcleo debido a la interacción de cargas opuestas entre el protón y el electrón.
😀 La Ley de Coulomb se utiliza para calcular la fuerza eléctrica entre el protón y el electrón, y la segunda ley de Newton se aplica para relacionar esta fuerza con la aceleración centrípeta.
😀 El momento angular es una cantidad clave en el modelo de Bohr, y Bohr postuló que debería ser cuantizado, tomando valores enteros de la forma n × h / 2π.
😀 La relación entre el momento angular cuantizado y la velocidad del electrón nos permite despejar la velocidad del electrón en la órbita.
😀 La ecuación para la velocidad del electrón, v, es igual a n × h / (2π × m × r), donde n es un número entero, h es la constante de Planck, m es la masa del electrón y r es el radio de la órbita.
😀 Tras realizar los cálculos, se obtiene un radio específico para la órbita del electrón en el estado fundamental (n = 1), que es aproximadamente 5.3 × 10⁻¹¹ metros.
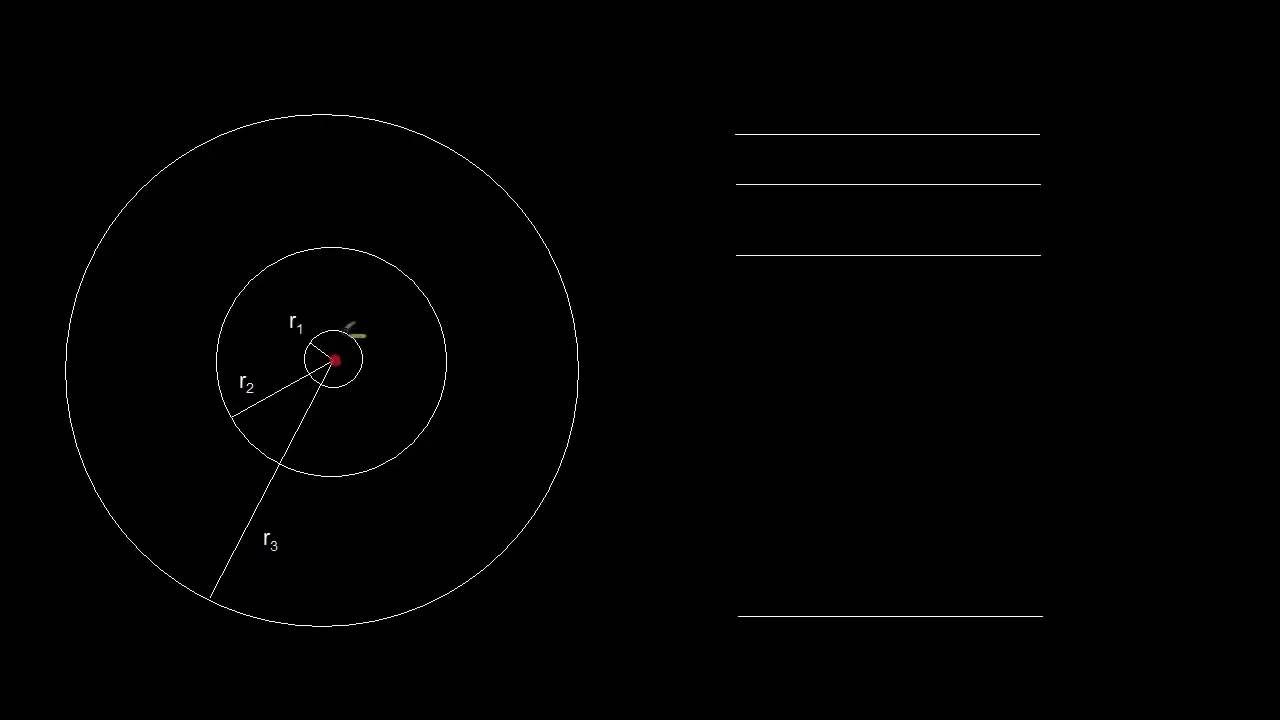
😀 El modelo de Bohr limita los radios posibles de los electrones a valores específicos, ya que el momento angular está cuantizado.
😀 La fórmula general para los radios de las órbitas del electrón en el modelo de Bohr es rₙ = n² × r₁, donde r₁ es el radio para el estado fundamental y n es un número entero.
😀 Este modelo establece que solo ciertos radios están permitidos, lo que implica que las órbitas de los electrones son discretas, no continuas.

Q & A

¿Cómo describe el modelo de Bohr el átomo de hidrógeno?
-El modelo de Bohr describe el átomo de hidrógeno con un protón en el núcleo y un electrón que orbita alrededor de él, similar a cómo los planetas orbitan alrededor del sol. Aunque no refleja completamente la realidad, este modelo es útil para calcular conceptos como el radio de la órbita del electrón.
¿Cuál es la fuerza que mantiene al electrón en su órbita según el modelo de Bohr?
-La fuerza que mantiene al electrón en su órbita es la fuerza eléctrica, que resulta de la atracción entre el electrón con carga negativa y el protón con carga positiva. Esta fuerza actúa como una fuerza centrípeta, que mantiene al electrón en movimiento circular.
¿Qué es la Ley de Coulomb y cómo se aplica en el modelo de Bohr?
-La Ley de Coulomb describe la fuerza eléctrica entre dos cargas. En el modelo de Bohr, se usa para calcular la fuerza eléctrica entre el electrón y el protón. La ley establece que la fuerza es proporcional al producto de las cargas e inversamente proporcional al cuadrado de la distancia entre ellas.
¿Cómo se relaciona la fuerza centrípeta con la aceleración en el modelo de Bohr?
-La fuerza centrípeta es la fuerza que mantiene al electrón en su órbita circular. En el modelo de Bohr, esta fuerza es igual a la masa del electrón multiplicada por su aceleración centrípeta, la cual está dada por la velocidad tangencial del electrón dividida entre el radio de la órbita.
¿Qué es el momento angular y cómo se utiliza en este modelo?
-El momento angular es una propiedad física que describe el movimiento rotacional de un objeto. En el modelo de Bohr, el momento angular del electrón se cuantiza y se establece que el momento angular es igual a un número entero (n) multiplicado por la constante de Planck (h), dividido por 2π.
¿Por qué Bohr cuantizó el momento angular del electrón?
-Bohr cuantizó el momento angular del electrón para explicar por qué los electrones solo pueden ocupar ciertas órbitas permitidas. Al hacerlo, limitó los valores posibles para el radio de las órbitas, lo que resultó en los niveles de energía cuantizados que observamos en los átomos.
¿Cómo se calcula la velocidad del electrón en el modelo de Bohr?
-La velocidad del electrón se calcula usando la relación entre el momento angular cuantizado y la masa del electrón. La fórmula obtenida es V = n * h / (2π * m * r), donde n es un número entero, h es la constante de Planck, m es la masa del electrón, y r es el radio de la órbita.
¿Qué fórmula se obtiene para el radio de la órbita del electrón en el modelo de Bohr?
-La fórmula para el radio de la órbita del electrón en el modelo de Bohr es r = n² * h² / (4 * π² * m * e² * K), donde n es un número entero, h es la constante de Planck, m es la masa del electrón, e es la carga elemental, y K es la constante de Coulomb.
¿Qué significa que los radios en el modelo de Bohr estén cuantizados?
-Que los radios estén cuantizados significa que el electrón solo puede ocupar ciertas órbitas específicas, cada una con un radio determinado. Estos radios están relacionados con los valores enteros de n, lo que implica que solo ciertos radios son permitidos, y no existen órbitas intermedias.
¿Cuál es el valor del radio de la órbita más pequeña en el modelo de Bohr?
-El radio de la órbita más pequeña, correspondiente al estado fundamental del electrón en el átomo de hidrógeno, es aproximadamente 5.3 * 10⁻¹¹ metros. Este valor se obtiene al sustituir los valores numéricos en la fórmula del radio y calcular para n = 1.