Intro to the Laplace Transform & Three Examples
Summary
TLDREste video forma parte de una serie sobre la transformada de Laplace, explicando su definición y cómo se aplica para resolver ecuaciones diferenciales. A lo largo de tres ejemplos, el video muestra cómo la transformada convierte ecuaciones diferenciales en ecuaciones algebraicas más fáciles de resolver. Los ejemplos incluyen funciones exponenciales, funciones escalonadas y polinomios, introduciendo también la función gamma. Se destaca la importancia de la convergencia y se ofrece una base sólida para entender y aplicar la transformada de Laplace en matemáticas y física.
Please replace the link and try again.
Q & A
¿Qué es la transformada de Laplace y por qué es útil?
-La transformada de Laplace es una herramienta matemática que convierte ecuaciones diferenciales en ecuaciones algebraicas. Esto permite resolver ecuaciones diferenciales de manera más sencilla, especialmente aquellas con derivadas, al transformarlas en una nueva ecuación sin derivadas.
¿Cómo se define la transformada de Laplace?
-La transformada de Laplace se define como una integral impropia desde 0 hasta infinito de la función f(t) multiplicada por e^(-st), donde 's' es una variable compleja. El resultado es una nueva función F(s) que depende de 's'.
¿Cuál es el propósito de la transformada de Laplace en las ecuaciones diferenciales?
-El propósito de la transformada de Laplace es convertir una ecuación diferencial con derivadas en una ecuación algebraica, que es más fácil de resolver. Luego, se puede aplicar la transformada inversa de Laplace para obtener la solución de la ecuación original.
¿Cómo se calcula la transformada de Laplace de la función exponencial e^(at)?
-La transformada de Laplace de e^(at) se calcula usando la integral impropia desde 0 hasta infinito de e^(-st) * e^(at). Al combinar los exponentes, la integral se simplifica y se evalúa, lo que da como resultado 1 / (s - a), bajo la condición de que s > a.
¿Qué ocurre si s es menor o igual a a en la transformada de Laplace de e^(at)?
-Si s es menor o igual a a, la integral no converge y el resultado es una divergencia, es decir, la transformada no existe en ese caso.
¿Qué es una función escalón (o función de Heaviside) y cómo se utiliza en la transformada de Laplace?
-La función escalón, U(t - a), es 0 cuando t < a y 1 cuando t ≥ a. Se utiliza en la transformada de Laplace para modelar discontinuidades en funciones. La transformada de Laplace de U(t - a) es e^(-as) / s, siempre que a sea positivo.
¿Qué es la función gamma y cómo se relaciona con la transformada de Laplace?
-La función gamma es una extensión del factorial, definida como una integral impropia. En la transformada de Laplace, la función gamma aparece al calcular la transformada de t^n, ya que su valor está relacionado con los factoriales mediante la fórmula de la transformada.
¿Cómo se calcula la transformada de Laplace de un polinomio t^n?
-La transformada de Laplace de t^n se calcula usando la integral de e^(-st) * t^n. Mediante un cambio de variable, se obtiene una expresión que involucra la función gamma, lo que lleva al resultado final de n! / s^(n+1).
¿Qué propiedades tiene la función gamma al evaluarse en enteros positivos?
-La función gamma evaluada en un entero positivo n+1 es equivalente al factorial de n, es decir, Gamma(n+1) = n!. Además, Gamma(1) = 1 y la función gamma tiene propiedades recursivas que facilitan su cálculo en valores sucesivos.
¿Qué se espera aprender en el próximo video relacionado con la transformada de Laplace?
-En el próximo video, se explorarán tres propiedades importantes de la transformada de Laplace, que ayudarán a entender cómo manipular y utilizar mejor esta herramienta en la resolución de ecuaciones diferenciales.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

TRANSFORMADA Z - Parte 1: Definición (REVISAR DESCRIPCIÓN) | El Traductor
Modelado de Sistema Masa-Resorte-Amortiguador utilizando Laplace + Matlab Simulink
78. Qué son las ecuaciones de segundo orden, ecuaciones homogéneas y de coeficientes constantes
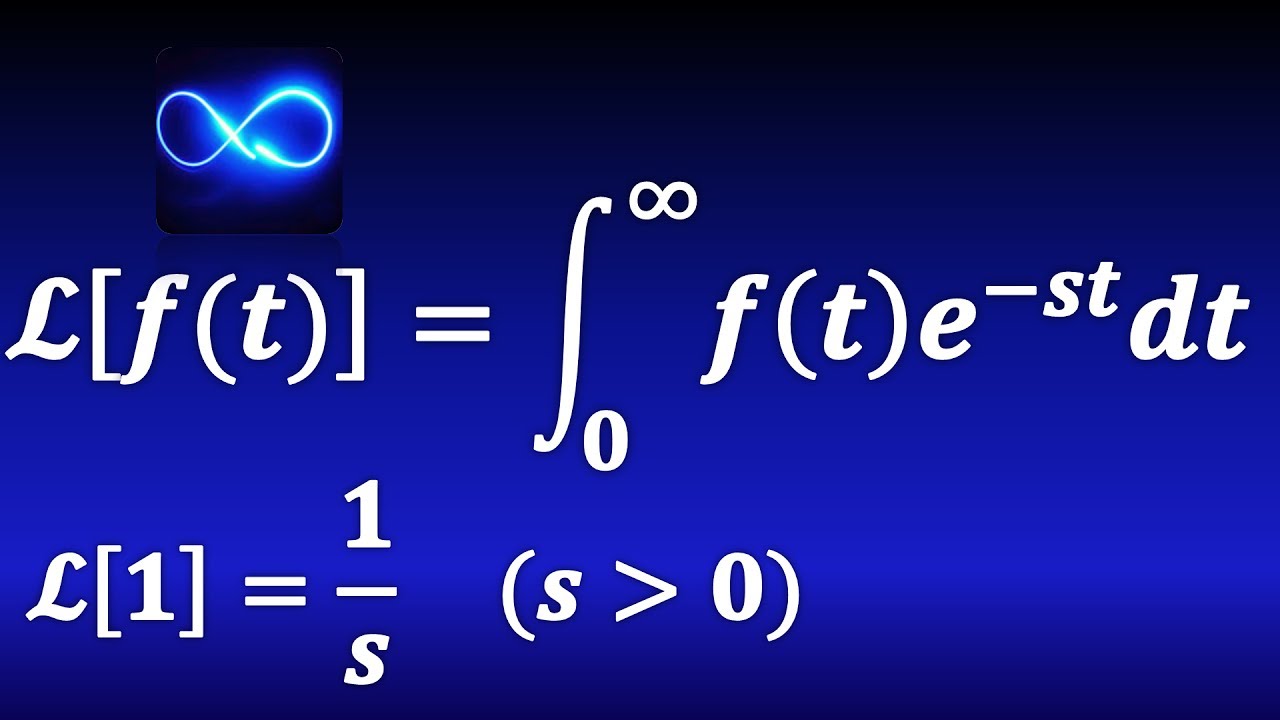
168. Transformada de Laplace: ¿qué es?. Definición, explicación y primer ejemplo.

Ecuaciones diferenciales | Introducción

Laplace con matlab. Vídeo 5

Transformada de Laplace #1 | Desde cero
5.0 / 5 (0 votes)