Lec 02 - Rational Numbers
Summary
TLDRThis lecture delves into the concept of rational numbers, distinguishing them from natural numbers and integers. It explains that rational numbers, often represented as fractions, can be expressed in multiple ways, unlike integers. The script highlights the process of reducing fractions to their simplest form by finding the greatest common divisor (GCD) through prime factorization. It also discusses the unique property of rational numbers being dense, meaning there is always another rational number between any two given rationals, contrasting with the discrete nature of integers. The lecture concludes by emphasizing the utility of rational numbers in arithmetic and comparisons, and their unique representation using the symbol Q.
Takeaways
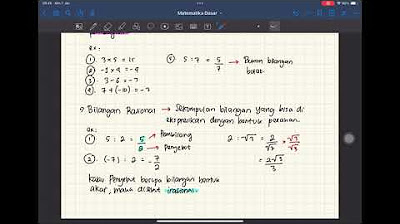
- 🔢 Rational numbers, also known as fractions, can be expressed as p divided by q, where both p and q are integers.
- 📏 The numerator (p) is the number above the fraction line, and the denominator (q) is the number below.
- 🌐 Rational numbers can be represented in multiple ways, unlike integers, which have a unique representation.
- 🔄 To compare or add rational numbers with different denominators, they must be converted to equivalent fractions with a common denominator.
- 🔢 The least common multiple (LCM) can be used to find a common denominator, but any common multiple will suffice.
- ➗ Rational numbers can be simplified to their reduced form by dividing both the numerator and the denominator by their greatest common divisor (GCD).
- 🔑 Prime factorization is a method used to find the GCD of two numbers, which helps in simplifying rational numbers to their reduced form.
- 🚫 Unlike integers, there is no concept of 'next' or 'previous' rational numbers because between any two rationals, another rational can always be found.
- 🔍 Rational numbers are dense on the number line, meaning there are no gaps between them, unlike integers which are discrete.
- 📚 The script uses the symbol 'Q' with double lines to denote the set of rational numbers, emphasizing their unique properties.
- ✂️ To summarize, rational numbers are ratios of two integers, they are not uniquely represented, and they lack a 'next' or 'previous' property due to their density.
Q & A
What is a rational number?
-A rational number is a number that can be expressed as the quotient or fraction p/q, where p and q are integers, and q is not zero.
Why can't we represent 19 divided by 5 as an integer?
-We cannot represent 19 divided by 5 as an integer because there is no integer k such that 5 times k equals 19.
How is the quantity 19 divided by 5 represented as a rational number?
-The quantity 19 divided by 5 is represented as a rational number as 3 and four-fifths, or as the improper fraction 19/5.
What is the special symbol used to denote rational numbers?
-The special symbol used to denote rational numbers is a double-lined Q, which looks somewhat unusual.
Why can the same rational number be written in many different ways?
-The same rational number can be written in many different ways because you can multiply or divide both the numerator and the denominator by the same non-zero integer and the value of the fraction remains unchanged.
How can you compare two fractions with different denominators?
-To compare two fractions with different denominators, you need to convert them into equivalent fractions with the same denominator, usually by finding a common multiple of the two denominators.
What is the least common multiple and how is it used in comparing fractions?
-The least common multiple (LCM) is the smallest number into which both denominators of two fractions can be multiplied to become factors of that number. It is used to compare fractions by making their denominators the same.
What is the reduced form of a rational number and why is it preferred?
-The reduced form of a rational number is when the numerator and denominator have no common factors other than 1. It is preferred because it provides a unique and simplified representation of the rational number.
How do you find the greatest common divisor (GCD) of two numbers?
-You can find the GCD of two numbers by using prime factorization, identifying the common prime factors, and multiplying them together.
Why can't we talk about the next or previous rational number in the same way we do for integers?
-We can't talk about the next or previous rational number because between any two rational numbers, there is always another rational number. This is due to the density of the rational numbers, unlike integers which are discrete.
What does it mean for numbers to be dense?
-Numbers are dense when there are no gaps between them. In the context of rational numbers, this means that between any two rational numbers, you can always find another rational number, such as by taking their average.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahora5.0 / 5 (0 votes)