Cómo y cuándo usar el Teorema del Seno - Parte 1
Summary
TLDREn este video, se explica el teorema del seno, también conocido como la ley del seno, que establece una relación de proporción entre los lados de un triángulo y el seno de sus ángulos opuestos. Se enseña cómo y cuándo utilizarlo, especialmente en casos donde se conoce un ángulo y dos lados o dos ángulos y un lado. A través de ejemplos prácticos, el video muestra cómo resolver triángulos aplicando esta ley, detallando el uso de proporciones y el cálculo de ángulos y lados desconocidos. Además, se introduce una breve mención al teorema del coseno como alternativa en ciertos casos.
Takeaways
- 😀 El teorema del seno establece una relación de proporción entre los lados de un triángulo y el seno de sus ángulos opuestos.
- 😀 Esta ley se enuncia comúnmente como a/sen(A) = b/sen(B) = c/sen(C), aunque se puede expresar de otras maneras.
- 😀 Es importante saber que esta relación ayuda a encontrar medidas de lados y ángulos en un triángulo cuando se dispone de algunos de ellos.
- 😀 El teorema del seno es útil en situaciones donde se conoce dos ángulos y un lado (AA' o ángulo-ángulo-lado) o dos lados y un ángulo opuesto a uno de esos lados (LAL).
- 😀 Si se tiene un triángulo con dos ángulos y un lado, se puede usar el teorema del seno para hallar el lado faltante o el ángulo faltante.
- 😀 Si nos dan dos lados y un ángulo no opuesto, se debe usar el teorema del coseno, lo cual será explicado en otro video.
- 😀 Para resolver un triángulo con el teorema del seno, se debe formar una proporción con los valores conocidos y despejar la incógnita.
- 😀 En los cálculos con el seno, si el valor obtenido es mayor que 1 o menor que -1, significa que el triángulo no puede ser construido.
- 😀 Al encontrar el valor de un ángulo usando el seno, se debe aplicar la función inversa seno^(-1) para determinar el ángulo correspondiente.
- 😀 Cuando se conocen dos ángulos, el tercero se puede obtener restando la suma de los ángulos conocidos de 180°, ya que la suma de los ángulos internos de un triángulo siempre es 180°.
- 😀 El cálculo de un lado faltante también puede hacerse usando el teorema del seno, aplicando la regla de tres con los lados y senos de los ángulos correspondientes.
Q & A
¿Qué es el teorema del seno?
-El teorema del seno establece una relación de proporción entre los lados de cualquier triángulo y el seno de sus ángulos opuestos. Esta relación permite encontrar medidas de lados y ángulos en un triángulo cuando se conocen ciertos datos.
¿Cómo se enuncia el teorema del seno?
-El teorema del seno se puede enunciar como sigue: a/sen(A) = b/sen(B) = c/sen(C), donde 'a', 'b' y 'c' son los lados del triángulo, y 'A', 'B' y 'C' son los ángulos opuestos a esos lados.
¿Cuándo se utiliza el teorema del seno?
-El teorema del seno se utiliza cuando se conocen dos ángulos y un lado de un triángulo (condición de Ángulo-Ángulo-Lado) o cuando se conocen dos lados y un ángulo (condición de Lado-Ángulo-Lado), con el ángulo opuesto a uno de los lados conocidos.
¿Cuáles son las condiciones necesarias para usar el teorema del seno?
-Para usar el teorema del seno, necesitamos tener al menos dos ángulos y un lado (Ángulo-Ángulo-Lado) o dos lados y un ángulo, donde el ángulo debe estar opuesto a uno de los lados conocidos.
¿Por qué no se puede usar el teorema del seno si el ángulo dado no está opuesto a uno de los lados conocidos?
-Si el ángulo no está opuesto a uno de los lados, no se puede aplicar el teorema del seno porque no se cumpliría la relación de proporción entre los lados y los senos de los ángulos, lo que haría imposible resolver el triángulo de manera adecuada.
¿Qué fórmula se utiliza para aplicar el teorema del seno en un ejercicio?
-La fórmula general del teorema del seno es a/sen(A) = b/sen(B) = c/sen(C), donde a, b y c son los lados del triángulo, y A, B y C son los ángulos opuestos a esos lados.
¿Qué sucede si el valor del seno de un ángulo en un cálculo es mayor que 1?
-Si el valor del seno de un ángulo es mayor que 1, significa que el triángulo no es posible o que hay un error en los cálculos, ya que el seno de un ángulo no puede exceder el rango de -1 a 1.
¿Cómo se encuentra un ángulo usando el seno de ese ángulo?
-Para encontrar un ángulo usando el seno, se debe aplicar la función inversa del seno (sen⁻¹) al valor obtenido en el cálculo. Esto se realiza en la calculadora para determinar el valor del ángulo correspondiente.
¿Qué sucede si tenemos los dos ángulos de un triángulo y uno de los lados?
-Si tenemos los dos ángulos de un triángulo y uno de los lados, podemos utilizar el teorema del seno para encontrar el tercer ángulo y luego aplicar el teorema para calcular los otros lados.
¿Qué se hace cuando se necesita encontrar el valor de un lado en un triángulo utilizando el teorema del seno?
-Para encontrar el valor de un lado, se organiza la proporción entre los lados y los senos de los ángulos correspondientes, se despeja la incógnita y se resuelve utilizando una regla de tres.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Cómo y cuándo usar el Teorema del Seno - Parte 2
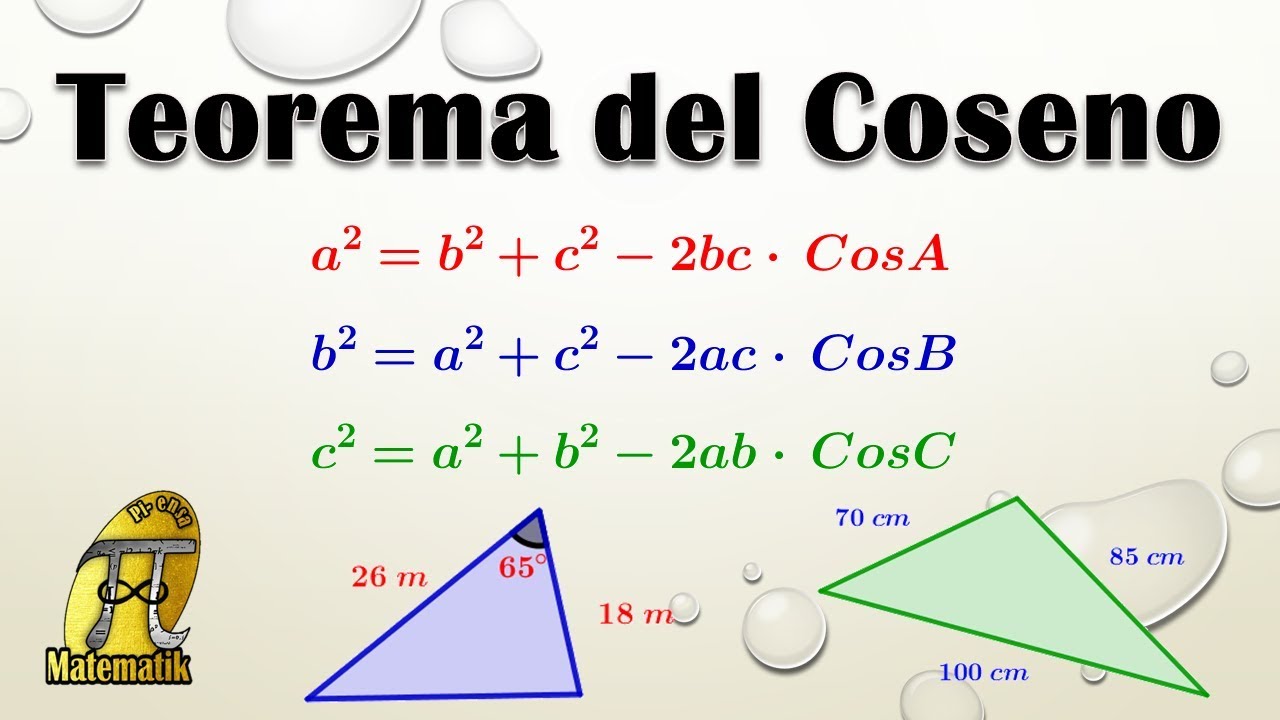
Cómo y cuándo usar el Teorema del Coseno - Parte 1

Ley de Senos | Ejemplo 1 Encontrar un lado

Ley de Senos | Introducción

Matemática 1 TRIGONOMETRÍA 2da parte funciones trigonométricas en triángulos cualquiera

Solucionar un triángulo rectángulo | Razones trigonométricas | Ejemplo 1
5.0 / 5 (0 votes)