Ecuaciones diferenciales simples
Summary
TLDREste video ofrece una introducción clara a las ecuaciones diferenciales, comenzando con el concepto básico de derivadas y diferenciales. Se explica cómo estas ecuaciones representan relaciones entre funciones y sus derivadas, y cómo las soluciones no son simplemente números, sino funciones que dependen de condiciones iniciales. A través de varios ejemplos prácticos, el video muestra cómo resolver ecuaciones diferenciales usando integrales y cómo determinar constantes para soluciones particulares. Además, aborda la diferencia entre las ecuaciones diferenciales ordinarias y las parciales, subrayando su importancia en diversas áreas de las matemáticas y las ciencias.
Takeaways
- 😀 Las ecuaciones diferenciales involucran cambios infinitesimales en las variables, representados por diferenciales como dy y dx.
- 😀 Una diferencial representa un cambio infinitamente pequeño, similar a la diferencia entre y y x, cuando estos se aproximan a cero.
- 😀 Resolver una ecuación diferencial implica encontrar una función, no solo un valor numérico.
- 😀 Las soluciones de ecuaciones diferenciales generalmente incluyen una constante arbitraria que puede determinarse con condiciones iniciales.
- 😀 La integral de una ecuación diferencial permite obtener la solución general, que puede incluir constantes de integración.
- 😀 La solución de una ecuación diferencial es una función que satisface la ecuación, y se determina por condiciones iniciales.
- 😀 Cuando se dan condiciones iniciales, como un valor específico para x y y, se puede determinar una solución particular para la ecuación diferencial.
- 😀 En algunos casos, como en la ecuación dy/dx = x/(y), es necesario manipular la ecuación, por ejemplo, multiplicando ambos lados por dx para poder integrarla.
- 😀 Al resolver ecuaciones con términos en x y y, las antiderivadas de cada lado de la ecuación deben ser calculadas por separado.
- 😀 Los ejemplos dados en el video ilustran cómo usar la integración para resolver ecuaciones diferenciales y cómo encontrar la constante de integración usando condiciones iniciales específicas.
- 😀 Cuando las soluciones involucran raíces cuadradas, es importante considerar las posibles soluciones positivas y negativas al tomar la raíz.
Please replace the link and try again.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Orden de una Ecuación Diferencial

Ecuaciones diferenciales | Introducción

0. ¿Qué es una Ecuación Diferencial? Tipos de ecuaciones diferenciales, solución de ED

ECUACIONES DIFERENCIALES EXACTAS. Curso completo de ecuaciones diferenciales desde cero

Cómo crear un modelo mediante Ecuaciones Diferenciales, lenguaje de funciones y derivadas
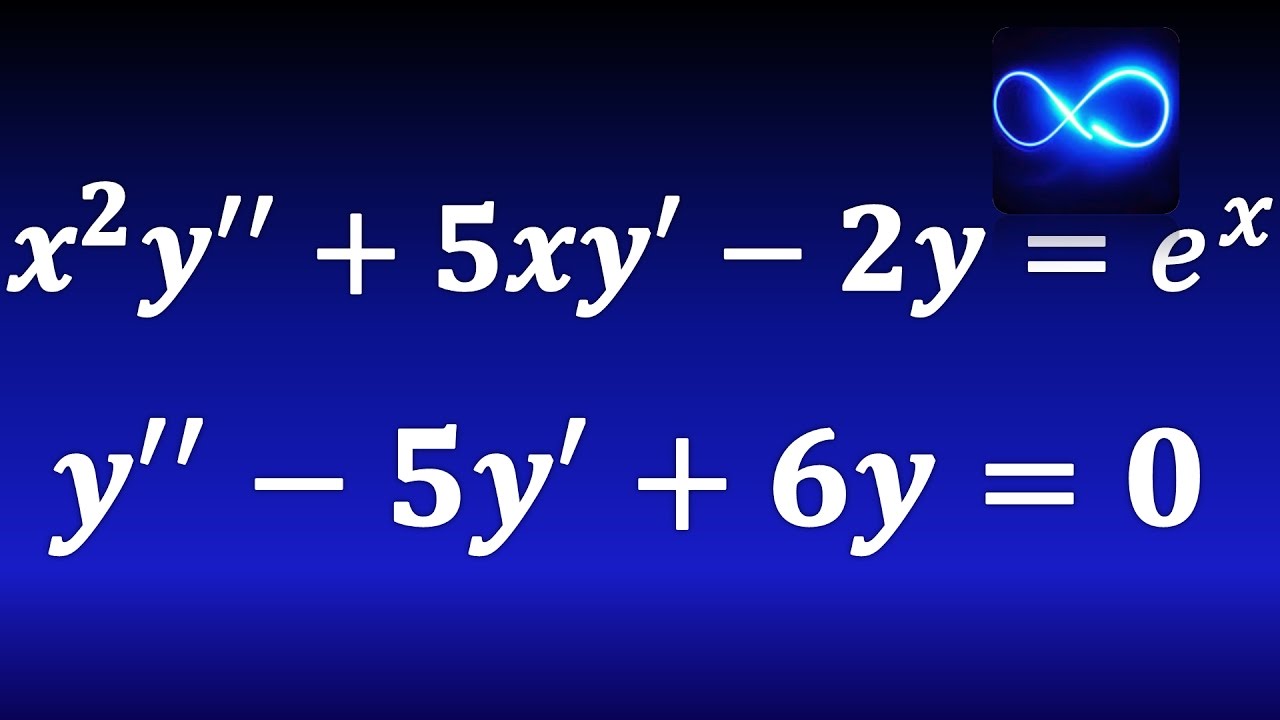
78. Qué son las ecuaciones de segundo orden, ecuaciones homogéneas y de coeficientes constantes
5.0 / 5 (0 votes)