ECUACIONES DIFERENCIALES EXACTAS. Curso completo de ecuaciones diferenciales desde cero
Summary
TLDREl guion del video ofrece una clase sobre ecuaciones diferenciales desde cero, enfocándose en el análisis de ecuaciones no homogéneas y no separables. Se introduce el concepto de ecuaciones diferenciales exactas y se demuestra cómo, mediante la verificación de ciertas condiciones, se pueden resolver de forma sencilla. Se utiliza un ejemplo práctico para ilustrar el proceso de integración y resolución de una ecuación diferencial exacta, mostrando los pasos para encontrar la función solución y cómo se relaciona con las derivadas parciales. Finalmente, se desafía a los estudiantes con un ejercicio similar para aplicar los conceptos aprendidos.
Takeaways
- 📚 Clase sobre ecuaciones diferenciales, introduciendo conceptos básicos y avanzados.
- 🔍 Primera clase enfocándose en ecuaciones diferenciales con variables separadas y fáciles de separar.
- 🔄 Segunda clase explorando ecuaciones diferenciales homogéneas y cómo convertirlas en variables separadas mediante un cambio de variable.
- 🆕 Tercera clase introduciendo ecuaciones diferenciales exactas, las cuales no tienen variables separadas y no son homogéneas.
- 📉 Una ecuación diferencial es exacta si la derivada de una función con respecto a otra variable es igual a la derivada de otra función con respecto a la primera variable.
- 🧩 Solución de ecuaciones diferenciales exactas implica encontrar una función que, cuando derivada, satisface la ecuación dada.
- 📝 Ejemplo práctico de resolución de una ecuación diferencial que no es separable ni homogénea, pero es exacta.
- 📉 Demostración de que la ecuación dada es exacta a través de la comparación de derivadas parciales.
- ✍️ Proceso de integración para encontrar la solución de la ecuación diferencial, incluyendo la adición de constantes.
- 🔢 Identificación de la solución en términos de las variables y constantes, y cómo se relaciona con la ecuación original.
- 📝 Asignación de un ejercicio similar a los estudiantes para practicar la solución de ecuaciones diferenciales exactas.
Q & A
¿Qué tipo de ecuaciones diferenciales se discutieron en la primera clase?
-En la primera clase se discutieron ecuaciones diferenciales en las que las variables estaban separadas o eran fácilmente separables.
¿Qué se aprendió en la segunda clase sobre ecuaciones diferenciales?
-En la segunda clase, se estudiaron ecuaciones diferenciales homogéneas que, a pesar de parecer desordenadas, podían ser transformadas en ecuaciones con variables separadas mediante un cambio de variable.
¿Cuál es el tema principal de la tercera clase de ecuaciones diferenciales?
-El tema principal de la tercera clase es el estudio de ecuaciones diferenciales que no tienen variables separadas y que no son homogéneas, conocidas como ecuaciones diferenciales exactas.
¿Qué propiedad verifican las ecuaciones diferenciales exactas?
-Las ecuaciones diferenciales exactas verifican la propiedad de que la derivada de la función 'm' con respecto a 'y' es igual a la derivada de la función 'n' con respecto a 'x'.
¿Cómo se define la solución de una ecuación diferencial exacta?
-La solución de una ecuación diferencial exacta es una función que satisface la condición de que la integral de 'm' con respecto a 'x' más la integral de 'n' con respecto a 'y' es igual a una constante.
¿Cómo se resuelve la ecuación diferencial dada en el ejemplo del script?
-Se resuelve integrando las partes de la ecuación y encontrando una función que, cuando derivada con respecto a 'x' o 'y', cumpla con las condiciones de la ecuación diferencial exacta.
¿Por qué se dice que la ecuación diferencial en el ejemplo es exacta?
-La ecuación diferencial en el ejemplo es exacta porque se verifica que la derivada de la función 'm' con respecto a 'y' es igual a la derivada de la función 'n' con respecto a 'x'.
¿Qué es una ecuación diferencial separable y cómo se diferencia de las ecuaciones exactas?
-Una ecuación diferencial separable es aquella en la que las variables pueden ser separadas y la ecuación se puede resolver integrando cada parte por separado. Mientras tanto, una ecuación diferencial exacta cumple una condición específica de igualdad de derivadas, que no es necesariamente el caso para las separables.
¿Qué es un cambio de variable y cómo se utiliza en ecuaciones diferenciales homogéneas?
-Un cambio de variable es una técnica utilizada para simplificar ecuaciones diferenciales, transformándolas en una forma más manejable. En el caso de ecuaciones diferenciales homogéneas, un cambio de variable puede permitir escribir la ecuación con variables separadas.
¿Cómo se puede determinar si una ecuación diferencial es homogénea o no?
-Una ecuación diferencial es homogénea si, después de un cambio de escala adecuado, todas las variables y coeficientes tienen el mismo exponente, generalmente uno. Si no se puede hacer esto, la ecuación no es homogénea.
¿Qué es el ejercicio propuesto al final del script y cómo se relaciona con el tema de la clase?
-El ejercicio propuesto es resolver una ecuación diferencial que no tiene variables separadas ni es homogénea, pero es exacta. Se relaciona con el tema de la clase ya que ejerce los conceptos aprendidos sobre ecuaciones diferenciales exactas.
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Variables Separables, video 1
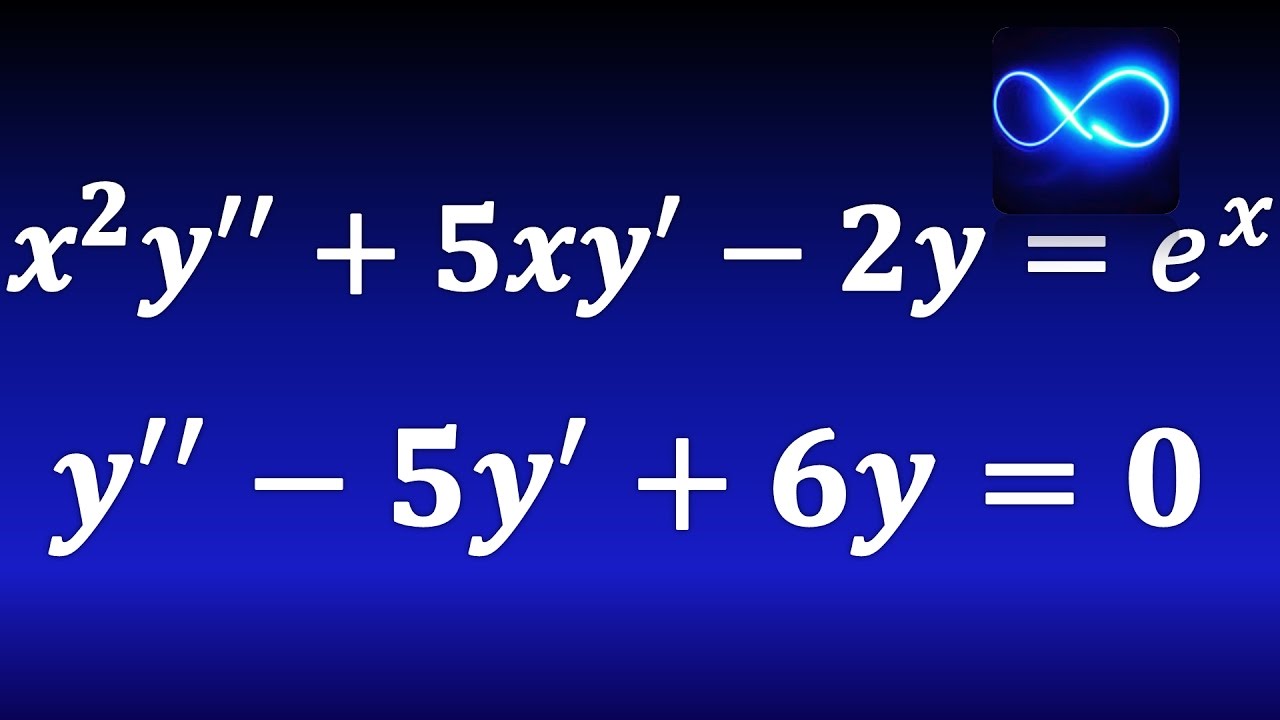
78. Qué son las ecuaciones de segundo orden, ecuaciones homogéneas y de coeficientes constantes

Ecuaciones diferenciales de variables separables | Introducción

Ecuaciones diferenciales simples

Orden de una Ecuación Diferencial

0. ¿Qué es una Ecuación Diferencial? Tipos de ecuaciones diferenciales, solución de ED
5.0 / 5 (0 votes)
