Kirchhoff's Voltage Law (KVL) Explained
Summary
TLDRIn this lesson, the focus is on Kirchhoff's Voltage Law (KVL), a fundamental principle in electrical circuit analysis. The law states that the sum of all voltages in a circuit is zero, which includes both the voltages produced and consumed. The video explains how to determine current direction, calculate voltages across resistors, and apply KVL to complex circuits with multiple voltage sources. Examples demonstrate the process, showing how to find current and voltage values and ensuring the sum of voltages is balanced. This lesson also sets the stage for understanding Kirchhoff's Current Law in the next video.
Takeaways
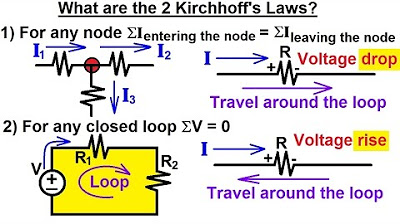
- 😀 Kirchhoff's Voltage Law (KVL) states that the sum of all voltages in a closed loop is equal to zero.
- 😀 The direction of current in a circuit is typically from the positive terminal to the negative terminal of the voltage source.
- 😀 If the current direction is unclear, an assumed direction can be used; a positive current value indicates the assumption was correct.
- 😀 Kirchhoff's Voltage Law is applied by adding up voltages across resistors and setting the sum equal to the supplied voltage.
- 😀 The voltage across each resistor is directly proportional to its resistance value in the circuit.
- 😀 In a simple circuit, KVL can be written as VT = V1 + V2 + V3, where VT is the source voltage and V1, V2, and V3 are the voltages across resistors.
- 😀 If the sum of the voltages results in a negative value, it indicates that the actual current direction is opposite to the assumption.
- 😀 KVL can be used to calculate the current in a circuit by dividing the total voltage by the total resistance.
- 😀 Multiple voltage sources in a circuit require careful application of KVL to determine current and voltages correctly.
- 😀 Kirchhoff's Voltage Law can be applied to circuits involving diodes and transistors, where voltage across components can be calculated using mesh equations.
Q & A
What is Kirchhoff's Voltage Law (KVL)?
-Kirchhoff's Voltage Law states that the sum of all voltages in a closed circuit is equal to zero. This means that the total voltage produced by sources in the circuit is equal to the sum of the voltages consumed by the circuit elements, such as resistors.
How do we determine the direction of current in a circuit?
-The direction of current is typically from the positive pole to the negative pole of a power source. However, if the current direction is not obvious, it can be assumed, and if the calculated current is positive, the assumption is correct. If negative, the direction is opposite to the assumed one.
What role do resistors play in a circuit when applying KVL?
-Resistors are circuit elements that consume voltage. When applying Kirchhoff's Voltage Law, the voltage across each resistor is added or subtracted depending on the current's direction and the resistor's orientation in the circuit.
How do we express Kirchhoff's Voltage Law mathematically in a simple circuit?
-In a simple circuit, Kirchhoff's Voltage Law is expressed as the equation: VT = V1 + V2 + V3, where VT is the total source voltage, and V1, V2, and V3 are the voltages across the resistors. Rearranging, it becomes -VT + V1 + V2 + V3 = 0.
Why is it important to use Kirchhoff's Voltage Law in circuit analysis?
-Kirchhoff's Voltage Law is fundamental to circuit analysis because it ensures that energy conservation is maintained, with the total energy supplied by sources equal to the energy consumed by resistors and other components.
How can Kirchhoff's Voltage Law be applied to find the voltage across each resistor in a circuit?
-To apply KVL, you sum the voltages across each resistor and equate the total to the source voltage. You can calculate the individual voltages using Ohm's Law (V = IR) and substitute into the KVL equation.
What is the significance of a negative current value when applying KVL?
-A negative current value means the current flows in the opposite direction to the initially assumed direction. This is confirmed by the sign of the current after solving the circuit equations.
What happens when two voltage sources are involved in a circuit?
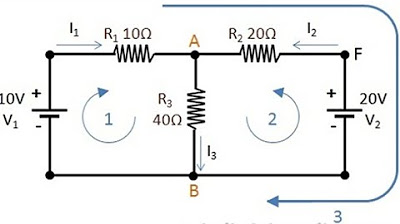
-When two voltage sources are present, Kirchhoff's Voltage Law can be applied by summing the voltages from both sources and the voltages across the resistors. The sum should still equal zero, considering the correct direction of the current and voltages.
How do you handle complex circuits with multiple resistors and voltage sources?
-In complex circuits, Kirchhoff's Voltage Law can be applied by breaking the circuit into smaller loops or meshes. For each mesh, you write a KVL equation and solve the system of equations to find the unknown values of current and voltage.
What is the relationship between the voltage across a resistor and its resistance?
-The voltage across a resistor is directly proportional to its resistance, according to Ohm's Law (V = IR). A higher resistance results in a higher voltage drop, given the same current.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
Electrical Engineering: Basic Laws (8 of 31) What Are Kirchhoff's Laws?

Kirchhoff's Voltage Law (KVL) - How to Solve Complicated Circuits | Basic Circuits | Electronics

KVL and KCL (Circuits for Beginners #11)

Chapter 2 - Fundamentals of Electric Circuits

Elektronika Dasar 002 Resistor 02 Universitas Jember
HUKUM II KIRCHHOFF
5.0 / 5 (0 votes)
