[SER222] M02_02 The Sorting Lower Bound (3/4): Putting it Together

Summary

En este video, se analiza cómo caracterizar la altura de un árbol de decisiones para determinar la cantidad mínima de trabajo necesario para ordenar cualquier entrada. A través de un árbol binario, se establece que el número de hojas es al menos N!, lo que implica que la altura del árbol, h, debe cumplir con la desigualdad N! ≤ 2^h. Aplicando aproximaciones, se llega a la conclusión de que el número mínimo de comparaciones necesarias para ordenar es al menos N log N, lo que establece un límite inferior en la complejidad de algoritmos de ordenamiento basados en comparaciones.

Takeaways

• 😀 La altura de un árbol de decisiones está directamente relacionada con el número de comparaciones necesarias para ordenar los datos.
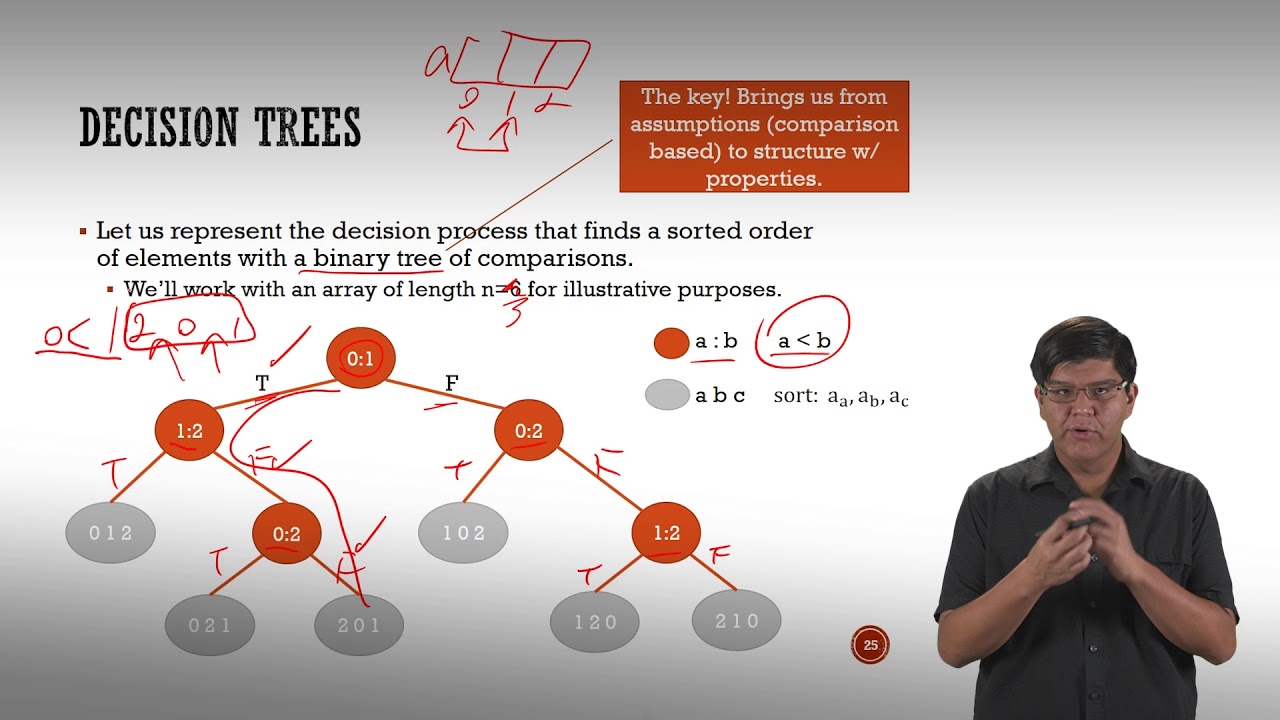
• 😀 El árbol de decisiones es binario, lo que significa que cada nodo representa una pregunta sí/no en el proceso de ordenación.
• 😀 El número de hojas en el árbol es igual al número de permutaciones posibles de los datos de entrada, que es N factorial (N!).
• 😀 En un árbol binario de altura h, el número máximo de hojas es 2^h.
• 😀 El número de hojas en el árbol debe ser al menos N!, ya que cada hoja representa una permutación única de los datos.
• 😀 La relación entre el número de hojas y la altura del árbol se expresa como N! ≤ 2^h, lo que nos da una base para calcular la altura.
• 😀 Usando logaritmos, podemos derivar la altura mínima del árbol a partir de la fórmula N! ≤ 2^h.
• 😀 La aproximación de Stirling se utiliza para simplificar el cálculo de log(N!) como aproximadamente N log N.
• 😀 La altura mínima del árbol de decisiones, que es el peor caso para ordenar, se determina como N log N.
• 😀 Este análisis establece un límite inferior (lower bound) para el número de comparaciones necesarias en el peor de los casos: al menos N log N comparaciones.
• 😀 La conclusión es que, para explorar todas las hojas del árbol y ordenar cualquier conjunto de datos, se requieren al menos N log N comparaciones.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.