PCA Algorithm | Principal Component Analysis Algorithm | PCA in Machine Learning by Mahesh Huddar
Outlines
Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap
Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords
Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights
Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts
Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
Python Exercise on kNN and PCA
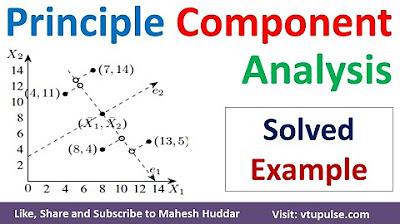
1 Principal Component Analysis | PCA | Dimensionality Reduction in Machine Learning by Mahesh Huddar
StatQuest: Principal Component Analysis (PCA), Step-by-Step
Principal Component Analysis (PCA) : Mathematical Derivation
StatQuest: PCA main ideas in only 5 minutes!!!
Principal Component Analysis (PCA) - easy and practical explanation
5.0 / 5 (0 votes)
