19.1 Introduction to Magnetic Fields and Forces | General Physics
Summary
TLDRThe video explains the right-hand rule in electromagnetism, demonstrating how to determine the direction of the magnetic force on charged particles in a magnetic field. It illustrates the force's dependence on the charge's direction of motion and the orientation of the magnetic field, using examples with positive and negative charges. The calculation of magnetic force is demonstrated, emphasizing its role in particle trajectories, particularly in circular motion. The tutorial also touches on further calculations involving acceleration and the radius of circular paths, making complex concepts accessible and engaging for students.
Takeaways
- 😀 The right-hand rule is a method used to determine the direction of magnetic forces on charged particles in a magnetic field.
- 😀 For a positive charge, the force direction is determined by pointing the fingers in the direction of the magnetic field and the thumb in the direction of velocity, with the force coming out of the palm.
- 😀 For a negative charge, the force direction is opposite, coming out of the back of the hand.
- 😀 When visualizing magnetic fields and velocities, it's important to represent directions that are out of or into the page using dots and Xs, respectively.
- 😀 In a scenario with a positive charge moving right in a magnetic field directed into the page, the resulting magnetic force will be directed upward.
- 😀 The magnitude of the magnetic force can be calculated using the formula F = qvB sin(θ), where θ is the angle between velocity and magnetic field directions.
- 😀 In cases where the velocity and magnetic field are at 90 degrees, sin(90) equals 1, simplifying the force calculation.
- 😀 The strength of the magnetic field can significantly affect the force; for example, 2.0 Tesla is much stronger than the Earth's magnetic field.
- 😀 When a charged particle enters a magnetic field, its trajectory can change, potentially resulting in circular motion due to the continuous magnetic force acting on it.
- 😀 Understanding the relationship between magnetic forces and centripetal force is crucial when analyzing the motion of charged particles in magnetic fields.
Q & A
What is the right-hand rule used for in electromagnetism?
-The right-hand rule helps determine the direction of the magnetic force acting on a charged particle moving in a magnetic field.
How does the right-hand rule differ for positive and negative charges?
-For a positive charge, the force is directed out of the palm of the hand, while for a negative charge, the force is directed out of the back of the hand.
What does a dot and an 'X' represent in the context of magnetic fields?
-A dot represents a magnetic field directed out of the page, while an 'X' represents a magnetic field directed into the page.
What formula is used to calculate the magnetic force acting on a charged particle?
-The magnetic force is calculated using the formula F = qvB sin(θ), where F is the force, q is the charge, v is the velocity, B is the magnetic field strength, and θ is the angle between the velocity and the magnetic field.
How does the angle θ affect the magnetic force?
-The angle θ affects the force's magnitude; when θ is 90 degrees, the sine function equals 1, maximizing the force.
What is the significance of a magnetic field strength of 2.0 Tesla?
-A magnetic field strength of 2.0 Tesla is significantly stronger than Earth's magnetic field, which is about 0.5 Gauss, indicating a strong magnetic influence on moving charges.
How can the direction of the magnetic force change for a charged particle in motion?
-The direction of the magnetic force changes as the velocity of the charged particle changes; this can result in the particle veering off its initial trajectory.
What is centripetal force in the context of circular motion in a magnetic field?
-Centripetal force is the force required to keep a charged particle moving in a circular path within a magnetic field, directed towards the center of the circle.
How do you calculate the radius of circular motion for a charged particle in a magnetic field?
-The radius can be calculated using the relationship F = mv²/r, where F is the magnetic force, m is the mass of the particle, v is its velocity, and r is the radius.
What practical challenges do students face when applying the right-hand rule during tests?
-Students often find it challenging to properly orient their hands according to the right-hand rule, leading to confusion about the directions of forces, especially in three-dimensional problems.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Force électromagnétique - 1: Force de Lorentz
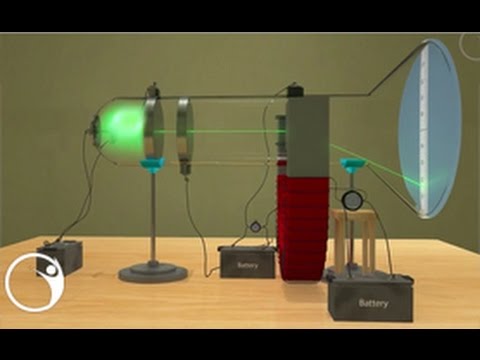
Determination of specific charge of an electron - Thomsons method

FISIKA Kelas 12 - Gaya Magnetik | GIA Academy
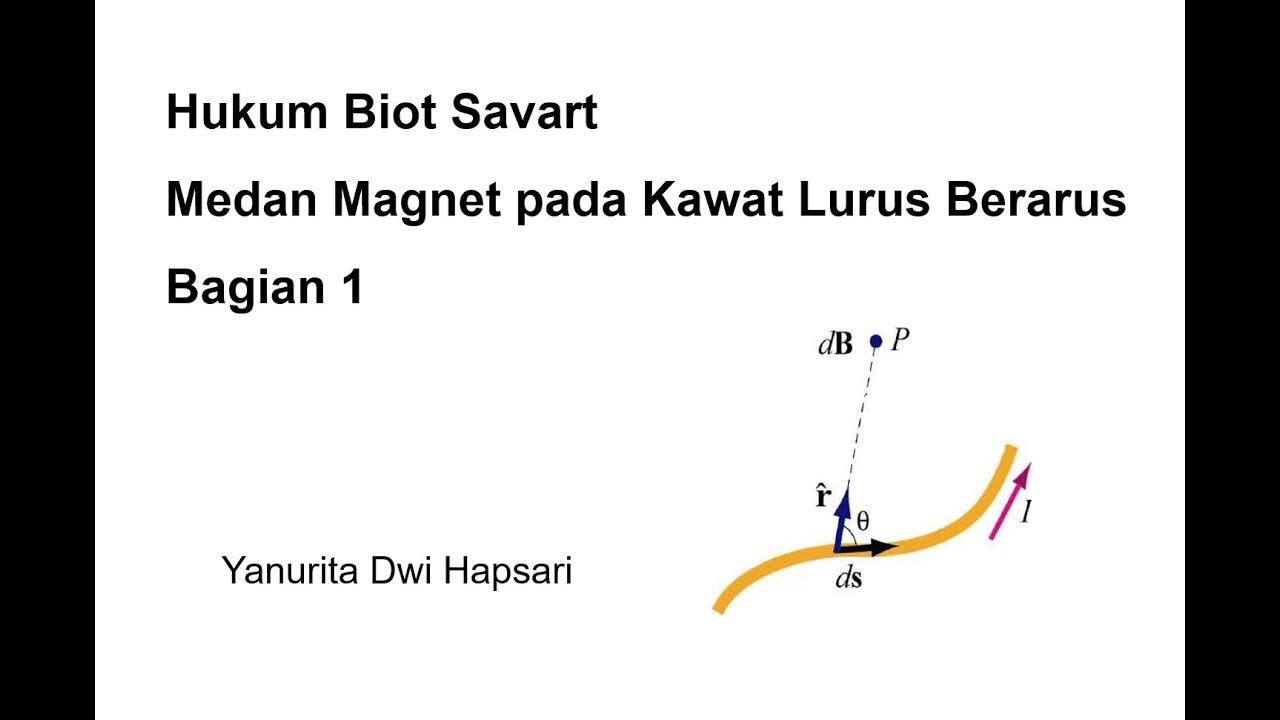
Hukum Biot Savart Bagian 1- Medan Magnet oleh Kawat Lurus Berarus - Fisika 2 Bab 4

Percobaan Gaya Lorentz Paling Gampang dan Jelas
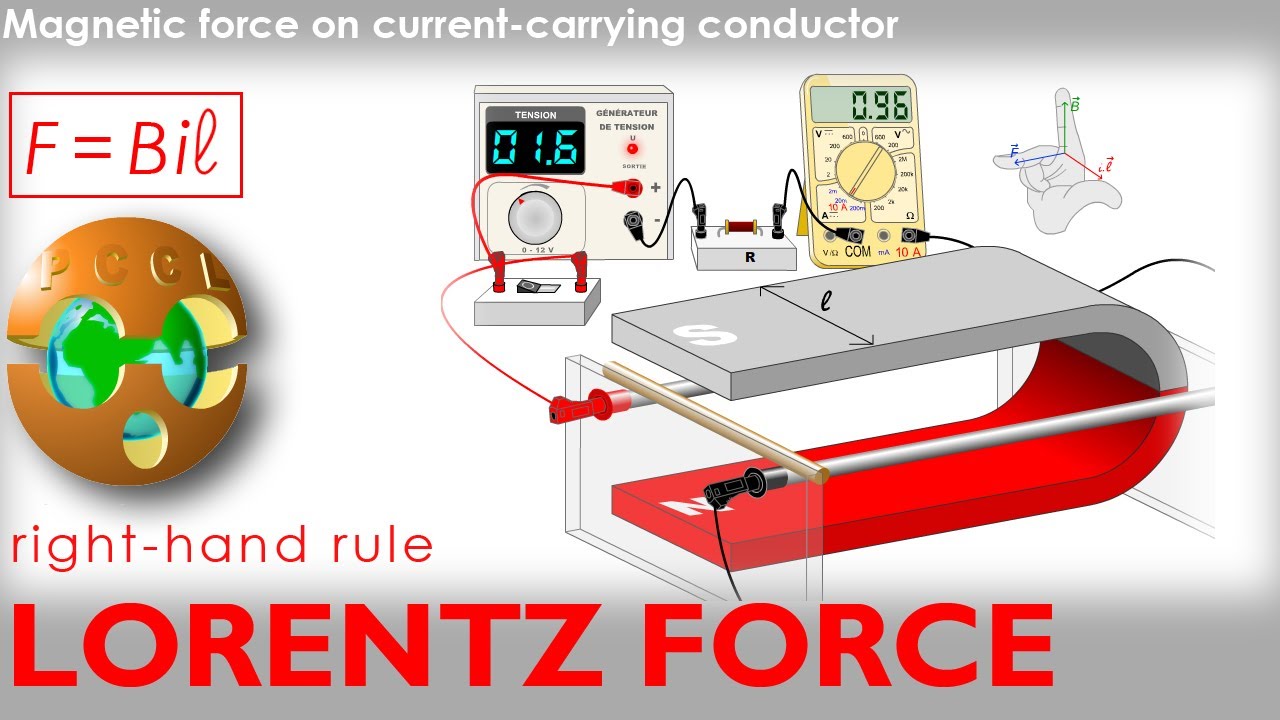
LORENTZ FORCE Rail + Rolling Conductor + i + Magnetic Field 🧲 + 3 Fingers Right Hand Rule 👆 PCCL
5.0 / 5 (0 votes)
