Invers dari Fungsi Komposisi
Summary
TLDREn este video educativo, se explica cómo encontrar el inverso de una composición de funciones. A través de ejemplos, se abordan conceptos clave como la composición de funciones y el cálculo de sus inversos utilizando reglas algebraicas. El video presenta dos funciones específicas y resuelve problemas paso a paso, destacando la importancia de aplicar las fórmulas correctamente para obtener los resultados. Se ofrece una explicación detallada para ayudar a los estudiantes a comprender cómo manipular funciones y sus inversos de manera efectiva.
Takeaways
- 😀 La inversa de una composición de funciones se obtiene invirtiendo el orden de las funciones involucradas.
- 😀 La regla general para la inversa de una composición de funciones es: (f ∘ g)^-1(x) = g^-1(x) ∘ f^-1(x).
- 😀 Para calcular la inversa de una composición, es necesario conocer primero las funciones individuales f(x) y g(x) y luego hallar sus inversas por separado.
- 😀 En el caso de la composición g ∘ f, la inversa será f^-1 ∘ g^-1.
- 😀 Para calcular la inversa de una función, primero se debe despejar la variable 'y' en términos de 'x' y luego resolver para 'x'.
- 😀 Si tienes una función como f(x) = (2x - 1)/(x + 1), se deben seguir pasos específicos como multiplicar cruzado para encontrar la inversa.
- 😀 Cuando se encuentra la inversa de una función compuesta, el proceso involucra sustituir la inversa de la función interna en la inversa de la función externa.
- 😀 En el ejemplo de f(x) = 5x - 1 y g(x) = x² - 3, la composición de estas funciones y su inversa fueron desglosadas paso a paso.
- 😀 Para resolver problemas con composiciones de funciones y sus inversas, es fundamental seguir un enfoque paso a paso, asegurándose de que cada paso sea lógico y claro.
- 😀 En el cálculo de la inversa, se deben manejar ecuaciones cuadráticas y fraccionarias con cuidado, usando técnicas como la factorización o el despeje de términos.
- 😀 Al practicar con ejemplos concretos y siguiendo los pasos establecidos en el tutorial, se puede lograr una comprensión más profunda de cómo manejar composiciones e inversas en matemáticas.
Please replace the link and try again.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Antiderivada e integral indefinida de una función

Función compuesta | Ejemplo 2

11. Integración de funciones trigonométricas inversas (cálculo integral)
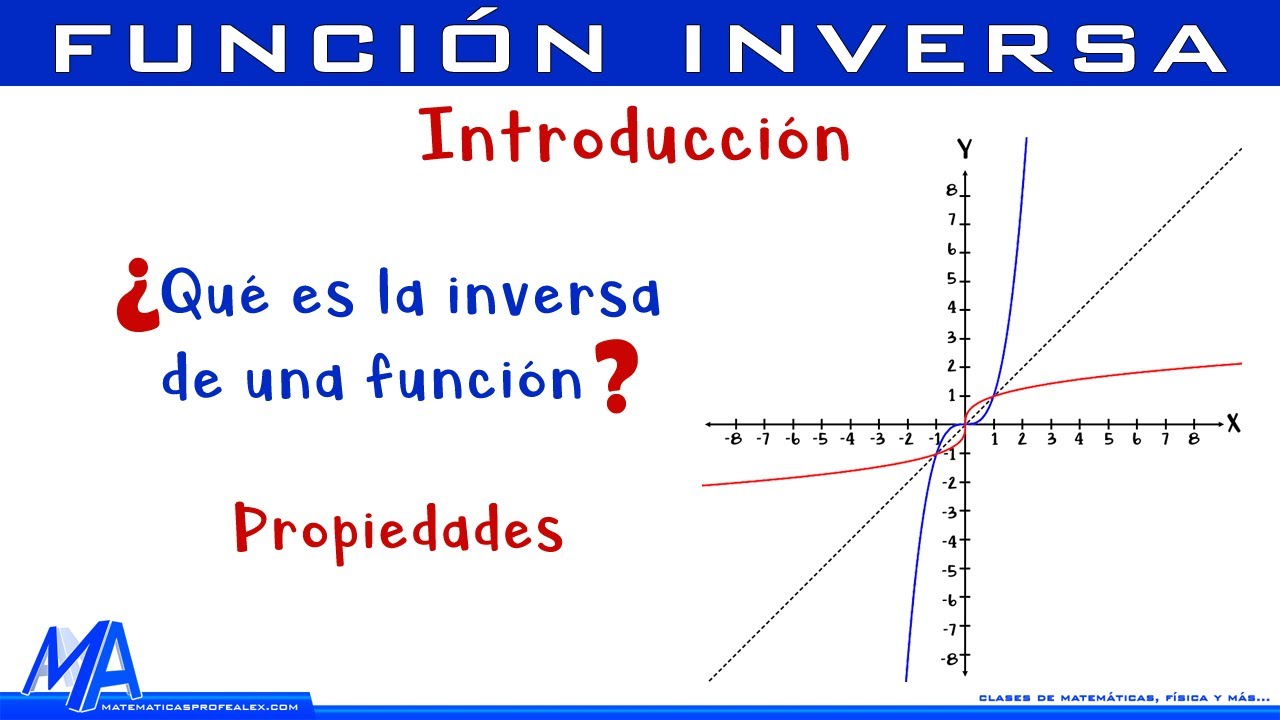
Función inversa | Introducción
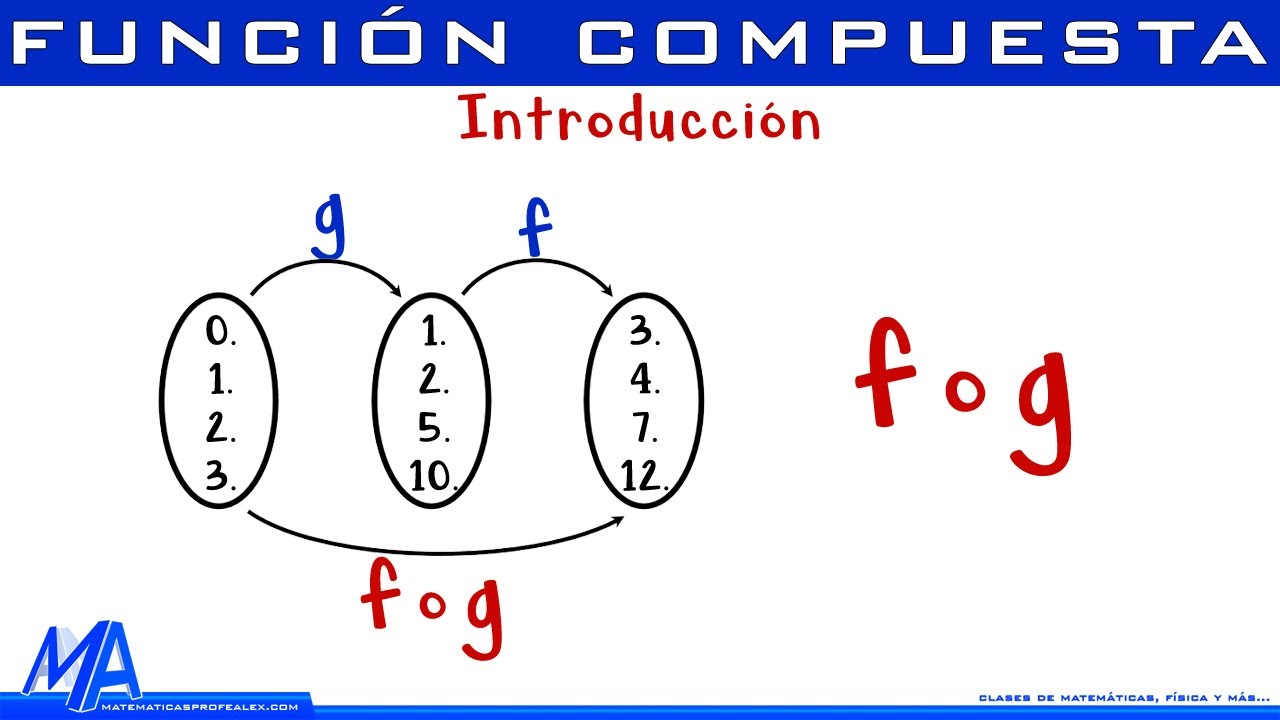
Función compuesta | Introducción

Evaluar funciones | Ejemplo 1
Mapa Topográfico, Acimut, Acimut Inverso y Distancia en Kilómetros...
5.0 / 5 (0 votes)