Inclined plane force components | Forces and Newton's laws of motion | Physics | Khan Academy
Summary
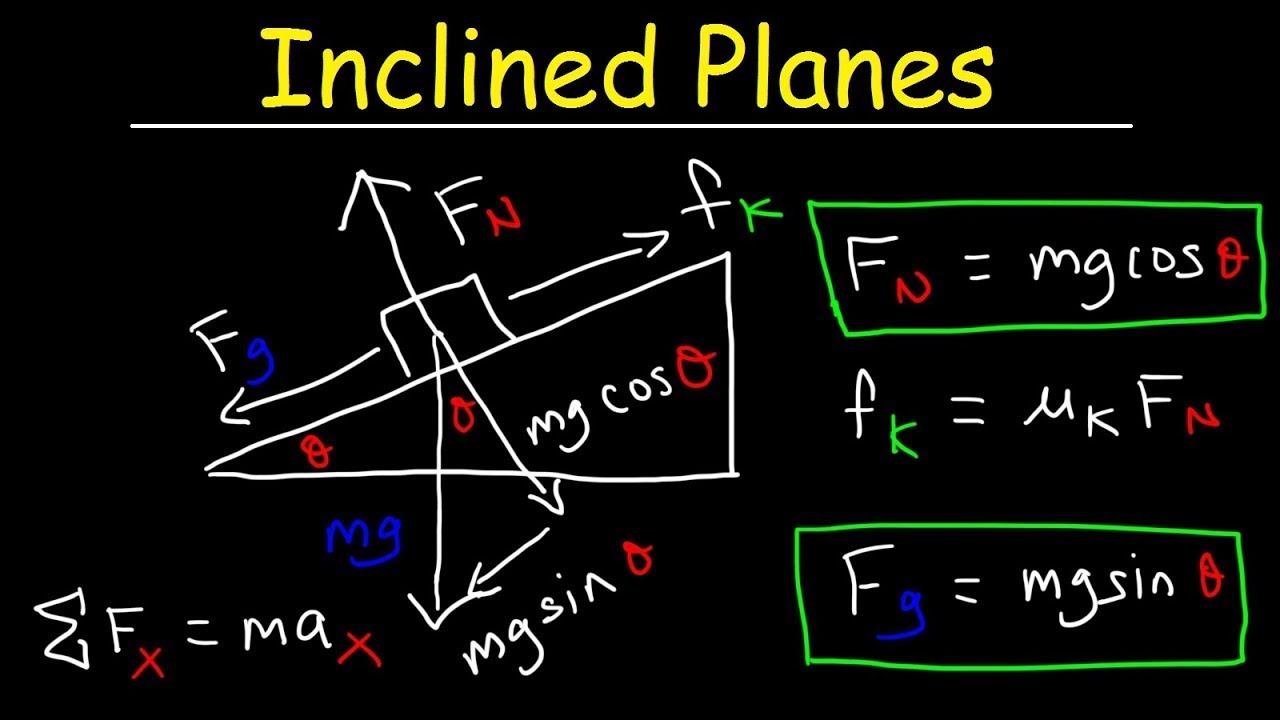
TLDRThe video script discusses the forces acting on a block with mass 'm' resting on an inclined plane. It introduces the concept of gravity's force pulling the block towards the Earth's center and explains how to break down this force into components: one perpendicular and one parallel to the ramp's surface. Using trigonometry, the script derives the magnitudes of these components in relation to the incline angle 'theta'. The perpendicular component is mg*cos(θ), and the parallel component is mg*sin(θ), where 'g' is the gravitational field near Earth's surface. The explanation aims to help viewers understand how these components can be used to analyze the block's potential motion on the inclined plane, considering normal force and frictional forces.
Takeaways
- 📐 **Gravity Force Decomposition**: The gravitational force acting on a block can be broken down into two components: one perpendicular to the inclined plane (ramp) and one parallel to it.
- 🌐 **Gravitational Field 'g'**: The force due to gravity on an object with mass 'm' is calculated as 'mg', where 'g' is the gravitational field near the Earth's surface.
- 🚫 **Normal Force Clarification**: The normal force acts perpendicular to a surface and is not directly against gravity when the surface is inclined.
- 🔽 **Downward Direction**: The force of gravity is directed downwards or towards the Earth's surface, regardless of the inclined plane's orientation.
- 📐 **Geometry and Trigonometry**: To understand the components of the gravitational force, one must use geometry to decompose the force vector and trigonometry to calculate the magnitudes of the components.
- 📐 **Inclined Plane Angle (θ)**: The angle of the inclined plane is crucial in determining the components of the gravitational force acting on the block.
- 🔄 **Parallel and Perpendicular Forces**: The perpendicular component of gravity is given by 'mg cos(θ)', and the parallel component by 'mg sin(θ)', where 'θ' is the angle of inclination.
- ➡️ **Parallel Force and Motion**: The parallel component of the gravitational force can cause the block to accelerate down the ramp if there is no opposing force, such as friction.
- 🧲 **Normal Force Balancing**: The normal force on the block may counteract the perpendicular component of gravity, keeping the block in place on the inclined plane.
- 🔀 **Force Balancing**: Understanding the balance between the forces acting on the block (gravity, normal force, and possibly friction) is essential for predicting its motion on an inclined plane.
- 📉 **Zero Angle Special Case**: When the inclined plane is horizontal (angle θ = 0 degrees), the perpendicular component of gravity equals the total gravitational force, and the parallel component is zero.
Q & A
What is the mass of the block mentioned in the script?
-The mass of the block is represented by the variable 'm'.
What force is acting on the block due to its position near the Earth's surface?
-The force acting on the block is gravity, which is represented as the product of the mass 'm' and the gravitational field 'g' near the Earth's surface.
What is the direction of the gravitational force acting on the block?
-The gravitational force is acting downwards towards the center of the Earth.
How does the normal force relate to the inclined plane and the force of gravity?
-The normal force acts perpendicular to the surface of the inclined plane and is not directly against the force of gravity, which is inclined at an angle theta to the surface.
What are the two components of the gravitational force that the script discusses?
-The two components of the gravitational force are the force perpendicular to the ramp (mg cos(theta)) and the force parallel to the ramp (mg sin(theta)).
What is the significance of breaking the gravitational force into components?
-Breaking the gravitational force into components allows us to analyze the separate effects of gravity on the block in terms of its potential motion along and perpendicular to the inclined plane.
How does the angle theta relate to the components of the gravitational force?
-The angle theta determines the magnitude of the components of the gravitational force. The force perpendicular to the ramp is mg times the cosine of theta, and the force parallel to the ramp is mg times the sine of theta.
What is the role of trigonometry in determining the components of the gravitational force?
-Trigonometry, specifically the SOH-CAH-TOA mnemonic, is used to calculate the magnitude of the components of the gravitational force acting on the block parallel and perpendicular to the inclined plane.
What happens if the inclined plane is perfectly horizontal (theta equals 0)?
-If the inclined plane is horizontal (theta equals 0), the force of gravity acting parallel to the plane becomes zero (since sine of 0 is 0), and the entire gravitational force acts perpendicular to the plane (cosine of 0 is 1).
What is the term for the force that would counteract the parallel component of gravity if the block is not moving down the plane?
-The term for the force that would counteract the parallel component of gravity is the normal force, which acts perpendicular to the surface of the inclined plane.
What might happen to the block if there is no friction and nothing to keep it from moving up the inclined plane?
-If there is no friction and nothing to keep the block from moving, the block may start accelerating down the inclined plane due to the parallel component of the gravitational force acting on it.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
Introduction to Inclined Planes
Plano inclinado con rozamiento (Bachillerato)

PIANO INCLINATO - piano inclinato fisica, reazione vincolare - Live Versione Corta
#fisica #diagramas #cuerpolibre FISICA - COMO SE REALIZA UN DIAGRAMAS DE CUERPO LIBRE?

Plano inclinado sem atrito

PEMBAHASAN SOAL-SOAL FISIKA HOTS SMA (1)
5.0 / 5 (0 votes)
