PIANO INCLINATO - piano inclinato fisica, reazione vincolare - Live Versione Corta

Summary

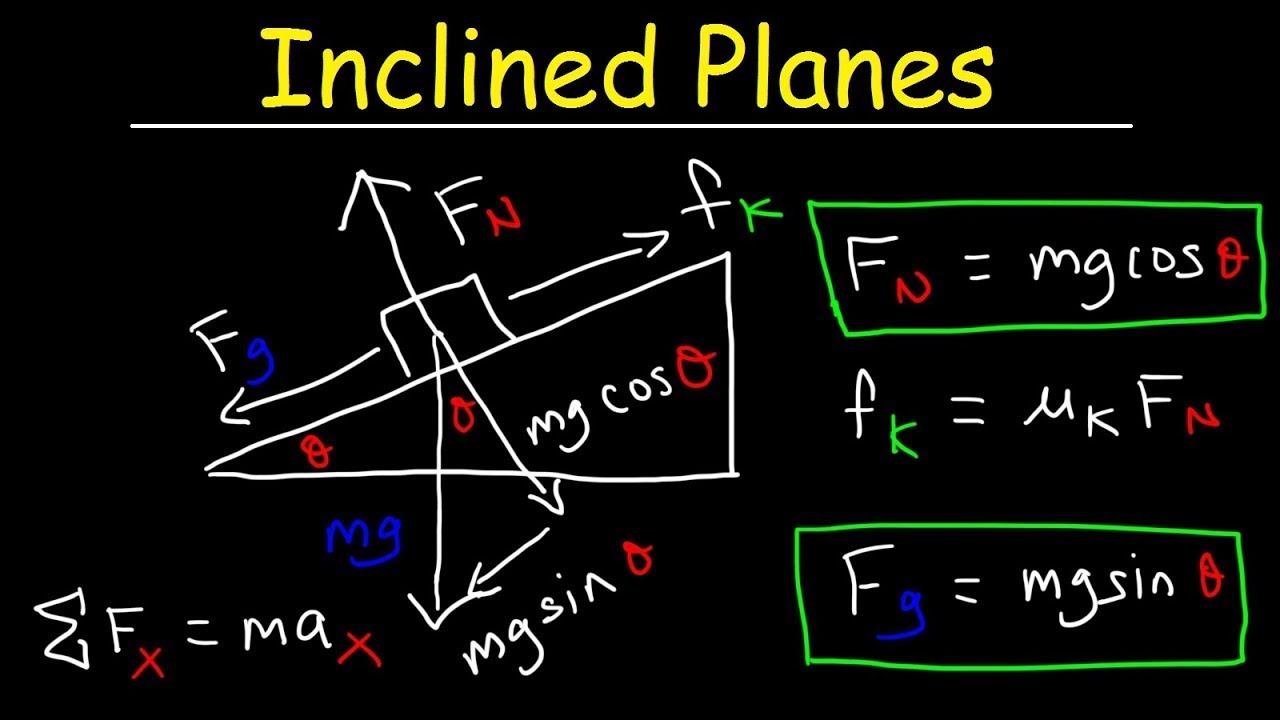
This physics lecture explains the forces acting on an object placed on a horizontal surface and an inclined plane. The speaker first discusses the weight force and the reaction force, which is always perpendicular to the surface. As the object moves to the inclined plane, the gravitational force is decomposed into parallel and perpendicular components. The parallel component causes the object to slide down the incline, while the perpendicular component balances with the reaction force. The lecture emphasizes the need for an equilibrium force to prevent motion, providing essential insights for solving inclined plane physics problems.

Takeaways

• 😀 The gravitational force (weight) always acts vertically downward on the object.
• 😀 The reaction force (normal force) is always perpendicular to the inclined plane and keeps the object from falling through the surface.
• 😀 When an object is placed on a horizontal plane, the only forces in play are the weight and the reaction force.
• 😀 On an inclined plane, the weight of the object must be decomposed into two components: one parallel and one perpendicular to the plane.
• 😀 The perpendicular component of weight is counteracted by the reaction force, resulting in no movement in that direction.
• 😀 The parallel component of the weight (parallel force) causes the object to slide down the inclined plane.
• 😀 To keep the object stationary on the inclined plane, a balancing force is required to counteract the parallel component of the weight.
• 😀 Friction or an external force can provide the balancing force that prevents the object from moving down the incline.
• 😀 The component of the weight parallel to the incline can be calculated using the formula: P_parallel = P * sin(α), where α is the angle of the incline.
• 😀 For equilibrium, the perpendicular forces (reaction force and perpendicular weight component) cancel out, leaving only the parallel component of weight to be dealt with.

Q & A

What is the significance of the weight vector in the discussion?

The weight vector represents the gravitational force acting vertically on the object. It is an essential component of analyzing the forces acting on an object in both horizontal and inclined scenarios.

Why is the reaction force described as being perpendicular to the inclined plane?

The reaction force is always perpendicular to the surface of the constraint (in this case, the inclined plane). This ensures that the object does not fall through the surface, and the reaction force counteracts the normal force of the object against the plane.

How does the reaction force differ from the weight force?

The weight force is always vertical, whereas the reaction force is perpendicular to the surface (inclined plane). The reaction force is not always directly opposite to the weight force because they act along different directions.

What happens when the object is placed on the inclined plane?

When the object is placed on the inclined plane, it is not in equilibrium and will begin to slide down due to the unbalanced component of the weight force that is parallel to the incline.

What does the instructor mean by the term 'equilibrating force'?

The equilibrating force is a force that counteracts the parallel component of the weight force, preventing the object from sliding down the incline. This force is equal in magnitude and opposite in direction to the parallel component of the weight.

How is the weight force split in the case of an inclined plane?

The weight force is decomposed into two components: one parallel to the incline (called the parallel component) and one perpendicular to the incline (called the perpendicular component).

What is the role of the perpendicular component of the weight force?

The perpendicular component of the weight force is balanced by the normal reaction force from the surface of the incline. This force does not contribute to the object’s movement along the incline.

Why is the object not in equilibrium on the inclined plane without the equilibrating force?

Without the equilibrating force, the parallel component of the weight force causes the object to slide down the incline, thus the forces are not balanced, and the object is not in equilibrium.

How do you calculate the equilibrating force?

The equilibrating force is calculated as the magnitude of the parallel component of the weight force. This force is equal and opposite to the parallel component, ensuring the object remains stationary on the incline.

What is the formula for calculating the parallel component of the weight force?

The parallel component of the weight force can be calculated using the formula: P_parallel = P * sin(α), where P is the weight of the object and α is the angle of the incline.