0625 Distribución hipergeométrica

Luis Rincón

16 Dec 201321:41

Summary

TLDREste video presenta una introducción a la distribución hipergeométrica, explicando su aplicación en un contexto de muestreo. Se describe el proceso de selección de objetos de dos tipos dentro de una urna, mostrando cómo calcular la probabilidad de seleccionar un número específico de objetos de un tipo dado. También se discuten las propiedades de la distribución, incluyendo su esperanza y varianza, y se concluye con un ejemplo práctico sobre la probabilidad de no seleccionar artículos defectuosos en una muestra. La presentación combina teoría y práctica para facilitar la comprensión del tema.

The video is abnormal, and we are working hard to fix it.
Please replace the link and try again.

Q & A

¿Qué es la distribución hipergeométrica?
-La distribución hipergeométrica describe el número de objetos de un tipo específico en una muestra tomada sin reemplazo de una población finita que contiene dos tipos de objetos.
¿Cuáles son los parámetros que definen la distribución hipergeométrica?
-Los parámetros son n (el total de objetos en la población), k (el número de objetos del primer tipo), y n' (el tamaño de la muestra).
¿Cómo se define la variable aleatoria X en el contexto de la distribución hipergeométrica?
-La variable aleatoria X se define como el número de objetos del primer tipo seleccionados en la muestra.
¿Cuál es la función de probabilidad de la distribución hipergeométrica?
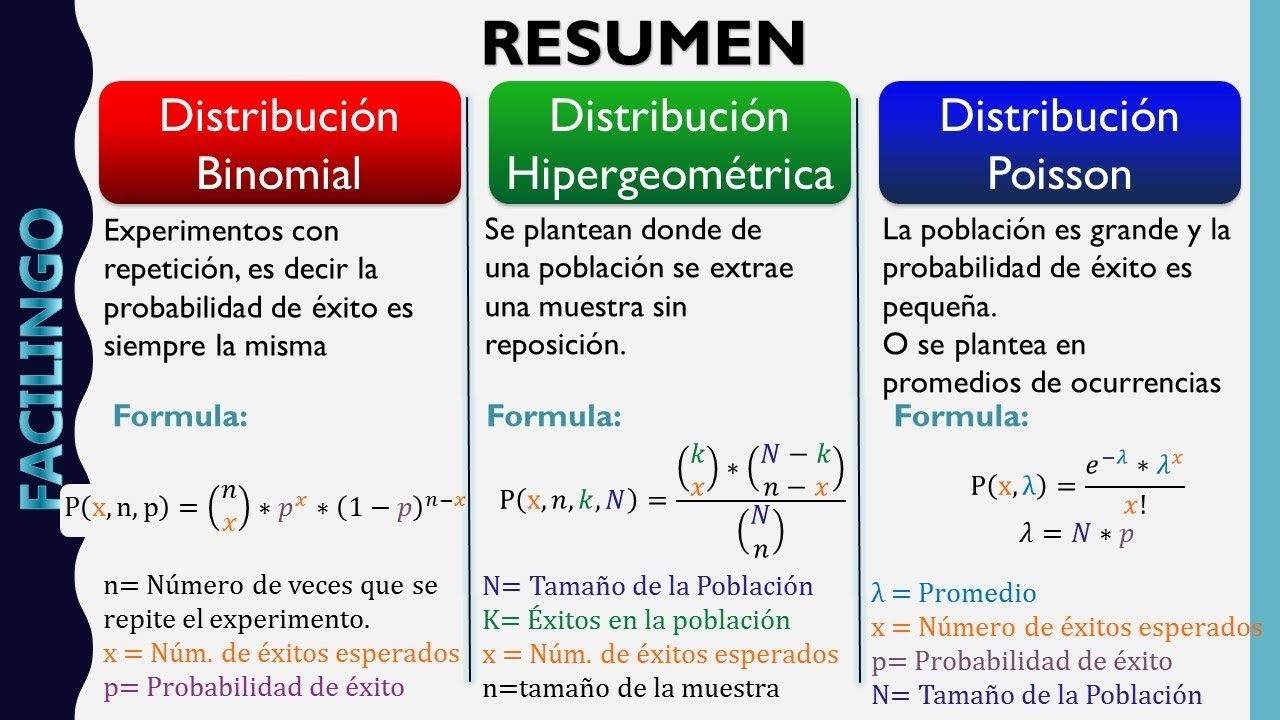
-La función de probabilidad se expresa como P(X = x) = (C(k, x) * C(n - k, n' - x)) / C(n, n'), donde C(a, b) representa el coeficiente binomial.
¿Cómo se verifica que la función de probabilidad es válida?
-Se verifica sumando las probabilidades para todos los posibles valores de x, que debe ser igual a 1, asegurando así que es una función de probabilidad.
¿Qué representa la esperanza de una variable aleatoria en la distribución hipergeométrica?
-La esperanza representa el valor esperado del número de objetos del primer tipo en la muestra y se calcula como E(X) = (n' * k) / n.
¿Cómo se calcula la varianza en la distribución hipergeométrica?
-La varianza se calcula usando la fórmula Var(X) = (n' * k * (n - k) * (n - n')) / (n^2 * (n - 1)).
¿Cuál es el contexto de un ejemplo práctico presentado en el video?
-Se presenta un ejemplo en el que se venden 75 artículos, de los cuales 10 son defectuosos, y se desea calcular la probabilidad de que al tomar una muestra de 5 artículos no aparezca ninguno defectuoso.
¿Qué fórmula se usa para calcular la probabilidad de que no haya artículos defectuosos en la muestra?
-Se utiliza P(X = 0) = (C(10, 0) * C(65, 5)) / C(75, 5) para calcular la probabilidad.
¿Por qué se usa la distribución hipergeométrica en lugar de la distribución binomial en este contexto?
-Se usa la distribución hipergeométrica porque el muestreo se realiza sin reemplazo, lo que significa que la probabilidad de seleccionar un artículo cambia después de cada selección.