Segitiga Bola Definisi
Summary
TLDRIn this educational video, the presenter explores the concepts of spherical geometry, focusing on the distinctions between great and small circles. It delves into the properties of spherical triangles, including their angle sums and side relationships, and provides formulas for calculating their area. The video further discusses Earth's coordinate system—latitude and longitude—and the implications of an observer's position in relation to celestial bodies. This comprehensive overview serves as a valuable resource for understanding fundamental principles of astronomy and geometry.
Takeaways
- 😀 The concept of a great circle and a small circle on a sphere is introduced, where the great circle's center coincides with the sphere's center.
- 😀 A spherical triangle is formed by the intersection of three great circles, analogous to a traditional triangle in Euclidean geometry.
- 😀 The properties of spherical triangles include that the sum of the angles is always greater than 180 degrees.
- 😀 To convert angles from degrees to radians, a conversion factor is applied, as 360 degrees equals 2π radians.
- 😀 The area of a spherical triangle can be calculated using the formula involving the excess of the triangle's angles.
- 😀 Movement along the same latitude corresponds to travel along a small circle on the sphere.
- 😀 Geographic coordinates consist of latitude (north/south of the equator) and longitude (east/west of the Prime Meridian).
- 😀 The height of celestial objects, like Polaris, correlates with the observer's latitude.
- 😀 Earth's shape is an oblate spheroid rather than a perfect sphere, which can be approximated with an ellipsoidal equation.
- 😀 The gradients and tangents of points on the ellipsoid can be determined using calculus to understand geographic positioning.
Q & A
What is the difference between a great circle and a small circle on a sphere?
-A great circle is defined as a circle on a sphere whose center coincides with the center of the sphere, while a small circle has its center not at the center of the sphere.
What defines a spherical triangle?
-A spherical triangle is formed by the intersection of three great circles on a sphere.
What is the relationship between the sides and angles of a spherical triangle?
-In a spherical triangle, the sum of the angles exceeds 180 degrees, and the sum of the lengths of any two sides is greater than the length of the remaining side.
How can the area of a spherical triangle be calculated?
-The area of a spherical triangle can be calculated using the formula: Area = Excess × R², where Excess is the sum of the angles in radians minus π.
What is the significance of latitude and longitude in geographical coordinates?
-Latitude measures the distance north or south of the equator, while longitude measures the distance east or west of the Prime Meridian, helping to pinpoint locations on the Earth's surface.
How does the position of an observer on Earth relate to celestial bodies?
-The height of celestial bodies, such as the North Star, observed by an observer corresponds to their latitude; for instance, at 30 degrees latitude, the North Star appears at 30 degrees above the horizon.
What is the relationship between the Earth's shape and its representation?
-The Earth is not a perfect sphere but rather an oblate spheroid, which can be approximated by an elliptical equation.
What is the conversion between degrees and radians?
-To convert degrees to radians, multiply by π/180; to convert radians to degrees, multiply by 180/π.
What are the maximum and minimum values for latitude and longitude?
-Latitude ranges from 0° at the equator to 90° at the poles, while longitude ranges from 0° at the Prime Meridian to 180° east and west.
What is the significance of the meridian lines on Earth?
-Meridian lines connect the North and South celestial poles, helping to define time zones and geographical coordinates on Earth.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
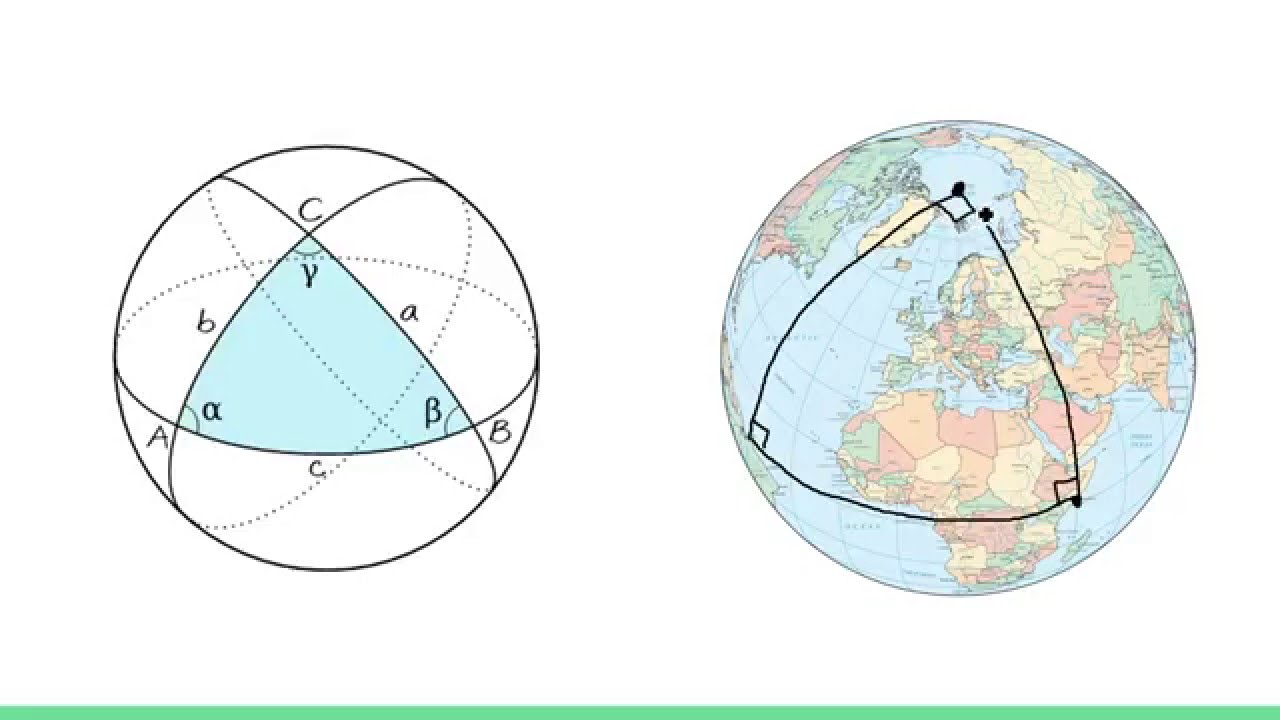
Spherical Geometry in Navigation

ATPL General Navigation - Class 4: Convergency.

Lingkaran dan Busur Lingkaran | #PekanBuktiKarya
Lingkaran (Bagian 1) - Unsur-unsur, Hubungan Sudut Pusat dan Sudut Keliling | SMP MTs Kelas VIII

Materi Lingkaran dan Busur Lingkaran Bab 2 Matematika Umum Kelas 11 SMA Kurikulum Merdeka
Garis Singgung Lingkaran (2) - Garis Singgung Persekutuan Luar dan Dalam - Matematika SMP
5.0 / 5 (0 votes)
