Eps.2 KALKULUS 2: Teknik Integrasi - Teknik Substitusi
Summary
TLDRThe video focuses on integral calculus, specifically the technique of substitution. It explains how substitution simplifies complex integrals by changing variables, highlighting its relevance in both high school and college mathematics. Key points include selecting the correct function for substitution, the importance of differentiating functions, and transforming integrals into simpler forms. The instructor provides examples to illustrate how to approach complex integrals by breaking them down into manageable parts. Additionally, the video discusses crucial tips for handling integrals with variable limits and emphasizes the importance of understanding complex forms to facilitate easier integration.
Takeaways
- 😀 Substitution technique is essential for simplifying complex integrals, commonly used even in high school.
- 📚 The chain rule is a fundamental principle in substitution, involving the differentiation of functions.
- 🔍 When choosing substitution variables, it is crucial to select the higher power in polynomial expressions to simplify the process.
- ⚠️ Be careful with variable boundaries when performing substitutions, as they can change the limits of integration.
- 🧠 Keep an open mind and think critically about integral forms; the initial complexity can often be simplified effectively.
- 🔄 The goal of substitution is to convert integrals into simpler forms that are easier to solve.
- 🔗 Use substitutions to transform integrals from one variable to another while maintaining the equivalence of the expressions.
- 🌟 Understanding the role of complex parts in integrals can help identify appropriate substitution strategies.
- ✏️ Example problems illustrate the importance of recognizing patterns, such as higher powers and their relationships in integrals.
- 🛠️ Substitution can act as a tool to break down complicated functions into manageable components for integration.
Q & A
What is the main topic of the lecture?
-The main topic is the technique of substitution in calculus, specifically in relation to integral calculus.
Why is substitution important in calculus?
-Substitution is important as it simplifies complex integrals, making them easier to solve by changing variables.
What is the first step in using the substitution technique?
-The first step is to identify a suitable substitution that simplifies the integral, usually selecting a function 'u' that is part of the integrand.
What does the chain rule have to do with substitution?
-The chain rule is used in substitution to relate the differential of the new variable 'u' to the original variable 'x', facilitating the integration process.
What type of integrals commonly require substitution?
-Integrals that involve complex functions, especially those that can be simplified by identifying a function and its derivative, often require substitution.
How does one decide which variable to substitute?
-Typically, the variable with the highest degree or the most complex expression is chosen for substitution to simplify the integral effectively.
What are some common mistakes to avoid when using substitution?
-Common mistakes include not properly adjusting the limits of integration when changing variables and incorrectly identifying the function to substitute.
How do you handle definite integrals when using substitution?
-When dealing with definite integrals, it's crucial to change the limits of integration according to the new variable after substitution.
Can substitution be applied to all integrals?
-No, substitution cannot be applied to all integrals; it is most effective for certain forms of integrals where simplification is possible.
What are some examples of integrals suitable for substitution?
-Examples include integrals involving polynomials multiplied by square roots or logarithmic functions, where selecting 'u' can significantly simplify the problem.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
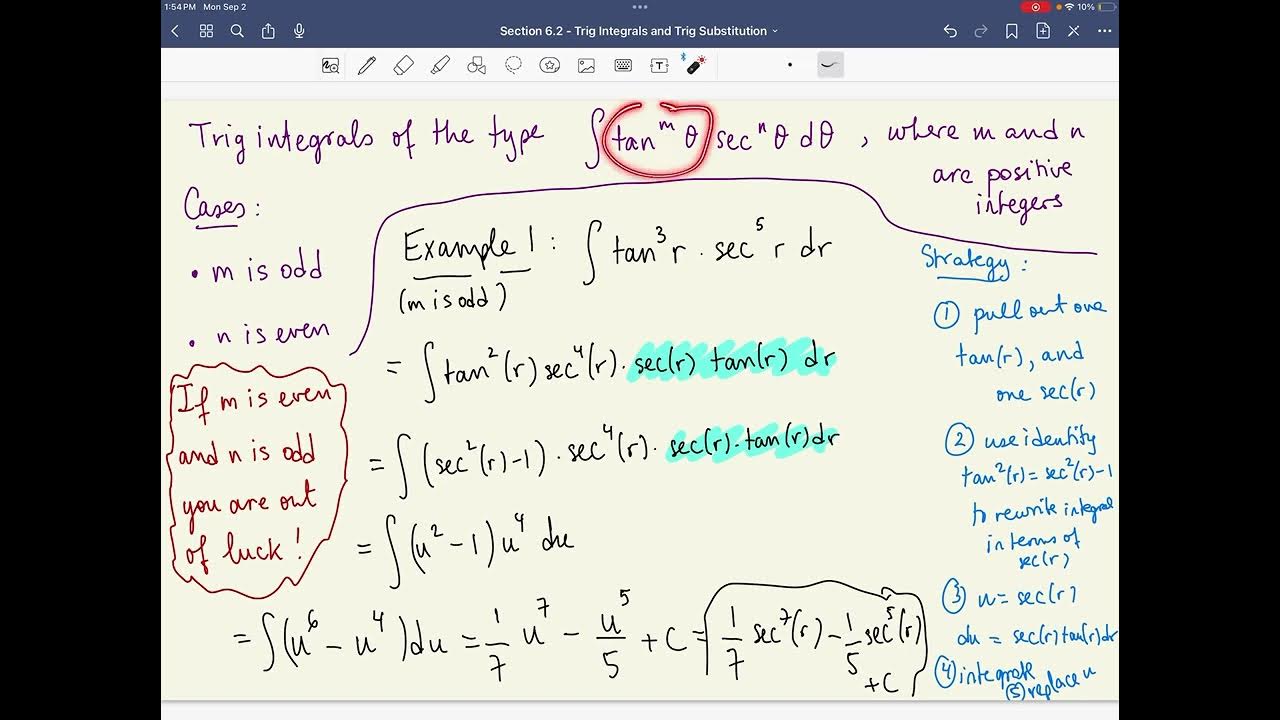
Section 6.2 - Trig integrals and substitution - Part 2
Kalkulus | Integral (Part 2) - Integral Substitusi [2]

MATEMATIKA Kelas 11 - Integral Tak Tentu | GIA Academy

Konsep Dasar Integral Fungsi Aljabar (Integral Part 1) M4THLAB

Integral Trigonometri Dasar, Substitusi & Menggunakan Identitas Trigonometri (Integral Part 6)

Kuliah Asinkron Matematika 2
5.0 / 5 (0 votes)
