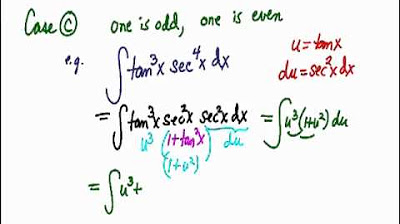Section 6.2 - Trig integrals and substitution - Part 2

Summary

This educational video script focuses on integral calculus, specifically integrals involving powers of tangent and secant functions. It outlines strategies for solving integrals when the power of tangent is odd or the power of secant is even, and when both conditions are met simultaneously. The script provides step-by-step examples, demonstrating how to simplify integral expressions using trigonometric identities and substitution methods. It emphasizes the importance of recognizing when the power of tangent is odd, which allows for the use of specific identities to simplify the integral. The tutorial is designed to help viewers understand and tackle complex integrals in calculus.

Takeaways

• 📚 The video discusses strategies for integrating functions involving powers of tangent and secant.
• 🔑 There are two straightforward cases: when the power of tangent is odd or the power of secant is even.
• ❌ If the power of tangent is even and the power of secant is odd, a generic strategy doesn't exist, and a case-by-case approach is needed.
• 🤔 The strategy involves pulling out one tangent or secant from the integral to simplify the expression.
• 🆚 For an odd power of tangent, after pulling out one tangent, the remaining power is even, allowing the use of a specific trigonometric identity.
• 🆓 The identity used is tangent squared equals secant squared minus one, which helps rewrite the integral in terms of secant.
• 🔄 A u-substitution is performed where u is secant, and du is secant tangent, simplifying the integration process.
• 📉 The integral is then integrated with respect to u, and the results are replaced back in terms of the original variable.
• 🔠 For an even power of secant, the strategy is to pull out secant squared and use the identity secant squared equals tangent squared plus one.
• 🔢 The final answer is expressed in terms of the original variable, with the integrated result adjusted for the pulled-out secant or tangent.

Q & A

What are the two cases where it is easy to solve integrals involving powers of tangent and secant?

It is easy to solve when the power of tangent is odd or the power of secant is even. If both conditions are met, either method can be used to find the correct answer.

Why is it helpful when the power of tangent is odd in solving integrals?

When the power of tangent is odd, you can pull out one tangent and then use trigonometric identities to simplify the remaining even power of tangent, making it easier to solve.

What is the first step when dealing with an integral where the power of tangent is odd?

The first step is to pull out one tangent and one secant from the integral. This allows you to work with an even power of tangent, which can be simplified using a trigonometric identity.

What trigonometric identity is used to simplify the integral after pulling out one tangent and secant?

The identity used is tangent^2(x) = secant^2(x) - 1, which allows you to rewrite the remaining even power of tangent in terms of secant.

Why is a substitution method used in these integrals, and what is the common substitution?

A substitution method is used to simplify the integral into a form that is easier to integrate. The common substitution is u = secant(x), where the derivative of secant is secant(x) * tangent(x), helping to reduce the complexity.

How do you rewrite the integral after the substitution u = secant(x)?

After substitution, the integral becomes a polynomial in terms of u, which can be expanded and integrated using basic rules of integration.

What happens if the power of tangent is even and the power of secant is odd?

If the power of tangent is even and the power of secant is odd, the integral becomes more difficult, and no generic strategy can be applied. Each case must be handled individually.

What is the strategy when the power of secant is even?

When the power of secant is even, the strategy is to pull out a factor of secant^2 and then use the identity secant^2(x) = 1 + tangent^2(x) to express the integral in terms of tangent.

How do you handle an integral where both tangent and secant have powers greater than 2?

In such cases, you first pull out secant^2 and use the identity secant^2(x) = 1 + tangent^2(x) to rewrite everything in terms of tangent, then proceed with substitution.

What is the final form of the integral after solving for an odd power of tangent and an even power of secant?

The final form of the integral is a polynomial in secant(x), which can be integrated and expressed in terms of secant(x) to a power, plus a constant (C).

Outlines

00:00

📚 Understanding Integrals Involving Tangent and Secant Powers

The video begins by introducing integrals that involve powers of tangent and secant. The key strategies are discussed for cases where the power of tangent is odd or the power of secant is even, and how to handle situations where both conditions apply. In cases where the power of tangent is odd, the method involves pulling out one tangent and one secant, rewriting the integral, and using trigonometric identities to simplify it. The instructor explains how to rewrite the integral in terms of secant using the identity for tangent squared and secant squared, and then applies u-substitution to solve the integral.

05:01

✏️ Applying U-Substitution and Completing the Integral

This section covers the step-by-step process of applying u-substitution to solve the integral. The instructor walks through distributing terms to integrate powers of u, solving for u, and then replacing u back with secant. The importance of the odd power of tangent is emphasized, as it allows the use of the identity for tangent squared. After completing the integration, the instructor showcases the final answer in terms of secant raised to different powers, highlighting the significance of the odd power of tangent for the method.

10:03

🔄 Example of Even Powers of Secant and Tangent

The final paragraph provides a contrasting example where the power of tangent is even, demonstrating a different approach. Here, the strategy focuses on pulling out secant squared and using the identity that relates secant squared to tangent. The integral is then rewritten entirely in terms of tangent, and the same u-substitution method is applied. The instructor solves the integral step-by-step, foiling terms before integrating, and concludes by replacing u with tangent to show the final result. The method's effectiveness for even powers of secant is emphasized.

Keywords

💡Tangent

Tangent refers to the trigonometric function often represented as tan(θ). In the context of the video, the focus is on integrating powers of the tangent function. Specifically, the script addresses how to handle cases where the power of tangent is odd, which allows the use of certain trigonometric identities to simplify the integral.

💡Secant

Secant, denoted as sec(θ), is another trigonometric function that is the reciprocal of cosine. The video emphasizes the integration of powers of secant and explains that it's easier to solve integrals where the power of secant is even. The script provides methods to manipulate and simplify expressions involving secant.

💡Power of tangent (odd)

This concept refers to cases where the tangent function is raised to an odd power. The video outlines a specific strategy for solving such integrals, which involves pulling out one tangent and using identities to simplify the remaining terms. The fact that the power is odd is crucial for the technique described.

💡Power of secant (even)

An even power of secant is discussed as a favorable case for integration. The video explains that when secant is raised to an even power, it allows for the application of trigonometric identities, such as secant-squared identity, to simplify the integral. This makes the integral easier to solve compared to cases with odd powers.

💡Trigonometric identity

A trigonometric identity is a mathematical equation that expresses one trigonometric function in terms of others. In the video, these identities are essential for transforming and simplifying the integrals. For instance, the identity tan^2(x) = sec^2(x) - 1 is used to replace tangent-squared terms with secant terms.

💡U-substitution

U-substitution is a method used in calculus to simplify the process of integration by making a substitution that turns a complicated integral into a more manageable one. In the video, this technique is applied by setting 'u' equal to secant, allowing the integral to be solved in terms of 'u' and its differential.

💡Derivative

A derivative measures the rate at which a function changes. In the context of the video, derivatives play a key role in finding integrals, particularly when performing u-substitution. For example, the derivative of secant is secant times tangent, which is used to simplify integrals involving these functions.

💡Integral

An integral is the inverse operation of differentiation and represents the area under a curve. The video specifically addresses how to solve integrals involving powers of tangent and secant, offering strategies for dealing with different cases based on whether the powers are odd or even.

💡Distribution

Distribution refers to the process of multiplying terms inside parentheses by a term outside the parentheses. In the video, distribution is used after making a u-substitution to simplify the resulting polynomial expressions, allowing the integral to be calculated term by term.

💡Trigonometric substitution

Trigonometric substitution is a technique used to evaluate integrals by substituting a trigonometric function for a variable to simplify the expression. In this video, tangent and secant are substituted in terms of each other using trigonometric identities to make the integration process easier.

Highlights

Two cases are highlighted for solving integrals involving powers of tangent and secant: when the power of tangent is odd, or the power of secant is even.

If the power of tangent is odd, one can pull out one tangent and one secant to simplify the integral.

The integral can be rewritten with the remaining terms as a function of the derivative of secant and tangent.

The identity involving tangent squared and secant squared is used to transform the integral into a more manageable form.

A U-substitution is performed with U as secant, allowing for an easier integration.

The integral of a function involving secant and tangent can be solved by expressing it in terms of secant alone.

The final answer is expressed in terms of secant to a certain power, showcasing the successful integration.

When the power of tangent is odd, the integral can be simplified by using the identity for tangent squared.

An example is provided where the power of secant is even, requiring a different approach.

In the case of an even power of secant, one can pull out a secant squared to simplify the integral.

The identity secant squared is equal to tangent of s plus 1 is used to rewrite the integral in terms of tangent.

A U-substitution with U as tangent is performed to integrate the function in terms of tangent.

The integral is solved by expressing it in terms of tangent and then integrating.

The final answer is expressed in terms of tangent to a certain power, completing the integration process.

The strategy for dealing with powers of tangent times powers of secant is outlined, emphasizing the importance of the power's parity.

Transcripts

[Music]

so now let's look at some integrals

involving powers of tangent and

secant so there are two cases in which

it's easy to do something and those

cases are if the power of tangent is odd

or the power of secant is

even okay or if it's both at the same

time like if this were even and this

were odd you could use either method and

again you're answer would look a little

different but they'd both be

correct if this is

even and this one is

odd no luck we don't know what to do

then you have to go on a Case by case

basis and see what you can do

okay so let's just do one example of

each one of those and we'll kind of put

the strategy on the right

here okay so let's first deal with the

um the uh possibility that the m is odd

so the power of tangent is odd okay so

what you're going to do is you're going

to pull

out one tangent so here I wrote the

variable as tangent of R just to get you

practicing the feeling of having

different variables so pull out one

tangent of whatever your variable is

here I'll WR R and one also

secant okay and I'm going to put them

together at the end

so this is what I mean so I'm going to

rewrite this integral I'm going to take

out one of the tangents here so I'll be

left with Tangent

squar and I'll have an extra tangent at

the

end and I'm going to pull out one of the

secants here so I'll have secant to the

5th sorry secant to the

4th and I'll just write this one

here so do you agree that that this is

equal to

this okay CU I have tangent * tangent

that's tangent cubed and secant to 4th

tangent squ time tangent is tangent

cubed and secant to 4th * secant gives

me secant to the 5th remember this is

not multiplication okay this is one

object object tangent of R cubed here's

a multiplication and this is another

object secant of R to the 5th okay why

was that helpful to me

because

this is going to play the role of my du

if that's my du what do you think my U

is going to be it's going to be

something whose derivative is secant

tangent and if you go back to our

first

page that was this so I'm going to have

a u being

secant that

means that I want everything left to be

in terms of secant

this is already in terms of cant so this

is good and this I need to

replace okay so the second part of my

strategy is use the

identity okay so let's go sorry to make

you a little nauseous here let's use the

identity involving tangent and secant so

this one so I'm going to replace

everything to do with Tangent squar by

secant 2us 1 so if

tangent + 1 is secant

squ I can subtract the one from both

sides and get this okay so I'm going to

use the

identity that tangent

squared in my case I have R is secant s

rus1 to rewrite my

integral in terms

of

secant okay so let's do it so this is

the integral of^ 2 R -1 * 4 of R time

secant R tangent

R doesn't really matter whether I wrote

tangent time secant or secant time

tangent I just wrote it in this

particular order because it's familiar

to us as a derivative okay if this had

been tangent to the

6th then I would first have written this

tangent squared

cubed and then replaced by this and I

would have had a cube

here okay so I want to see tangent

squared in my

integral okay and now I do my U

substitution I take U as

secant so du is secant

tangent everything's perfectly set up

for

me so this becomes the integral

of u^2 - 1

* U 4

du first I have to distribute to be able

to integrate U ^2 * U 4 is U the 6 -1 *

U 4th is U

4th I integrate and then I replace the U

I'll do it in two steps but you guys I'm

sure by now are already good at

this okay so I would integrate

and then in the end replace

you so then my final answer would be 17

U was secant this would be secant to the

7 in my case my variable was called R

minus

1 or I could write secant to the 5th

over 5 or 1 secant to the 5th plus C

okay so this would be my final answer

here

okay okay so that's the example if m is

odd if the power of tangent is odd it

mattered that it was odd because when I

took one out I had an even power of

tangent left which means I could use

this identity and even power can be

written as tangent squared to some power

this case it was just tangent squared

itself which allowed me to use this

identity so that's why it mattered that

my M was

odd okay so let's do one more example

like this

now I called my variable

s and you see this is not odd so if I

took out one of my tangents

here I'd be left with Tangent cubed and

then there's no way to use that identity

in terms of tangent squar of anything

okay so that's a nogo so instead I'm

going to use the fact that this is even

this is even and this were odd then I'm

in trouble hard integral okay then you

have to try to find some other way there

there's no generic strategy but if this

is even

now um my generic strategy is

to use the fact that I have an even

power of

secant so my strategy is to pull

out a secant squared of

something okay so let's do that here so

so I'm going to have tangent to

4th secant to 4th is the same as secant

s * secant

squ and then my idea is this is the

derivative of something this is the

derivative of

tangent okay so my second

part is to use the identity the same

identity so what would be good for me is

if everything here were written in terms

of tangent because that would be my U

and this would be my du so that's my

problem guy left that this is not in

terms of

tangent okay so I'm going to use the

identity that secant squ of

s

is tangent s of s +

1 okay that's the identity I'm going to

use and so in this

case so I'm going to use this to rewrite

the rest of my

integral in terms of

tangent okay so let's do that

here it's kind of fun somehow in a very

geeky sort of way okay so secant squ is

the same as tangent s s +

1 this I keep the same this du I keep

the

same and then I use a u

substitution U is

tangent so my du is secant

squ and I

integrate so this is U to 4th this is

u^2 + 1 this is

Du I have to foil before I integrate

this is U 6 Plus U 4 du

this is 17th U 7th + 1/5 U 5th if I make

a mistake along here you can check

me so and then finally after I integrate

I replace

you 17th my U was tangent I go back to

my original variable which was s in this

case tangent to the 5 of s plus c

okay okay so that's my strategy for

dealing with powers of tangent time

powers of secant