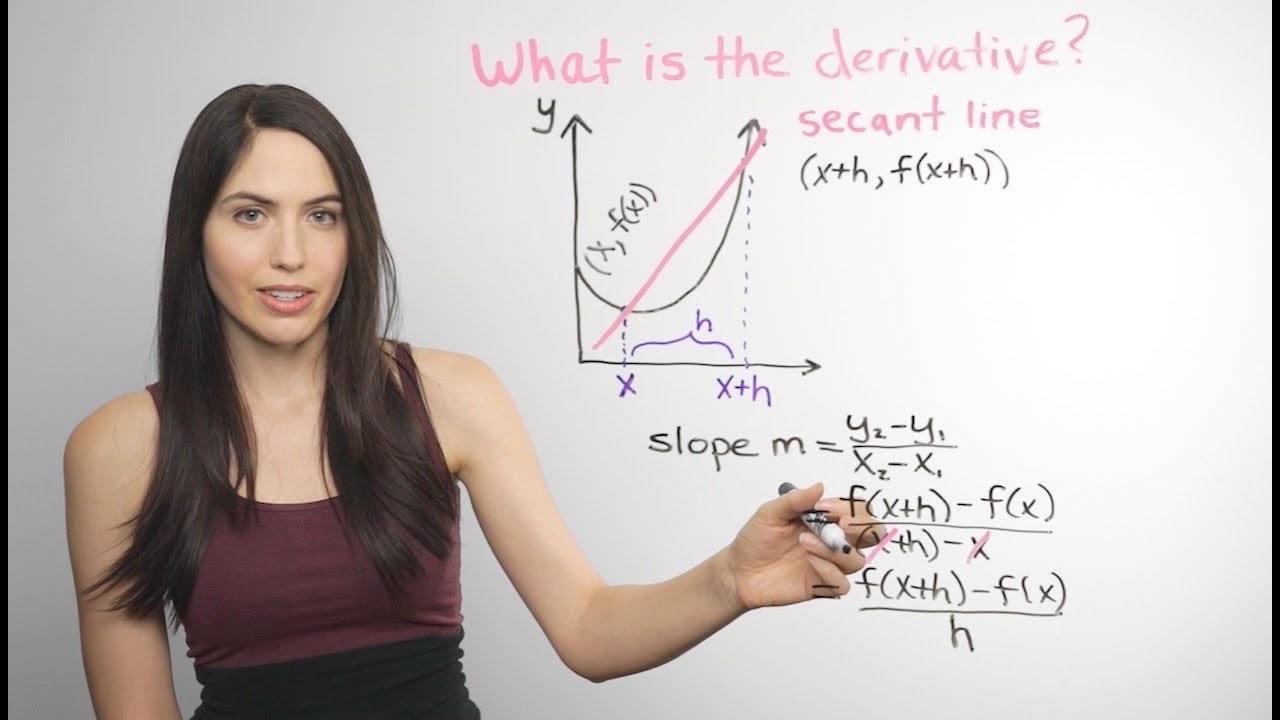12.2 Finding the derivative (PURE 1- Chapter 12: Differentiation)
Summary
TLDRThis section of Chapter 12 explains how to find the derivative of a function, which gives the exact gradient at any point on a curve. It starts with estimating the gradient using a tangent and then introduces the concept of limits to calculate it precisely. The derivative is based on the idea of a chord getting closer to a point as the distance tends towards zero, forming the foundation of calculus. The script walks through several examples and formulas, including differentiation from first principles, helping to visualize how the gradient of a curve is determined.
Takeaways
- 📈 The derivative is a function that provides the exact value of the gradient at any given point.
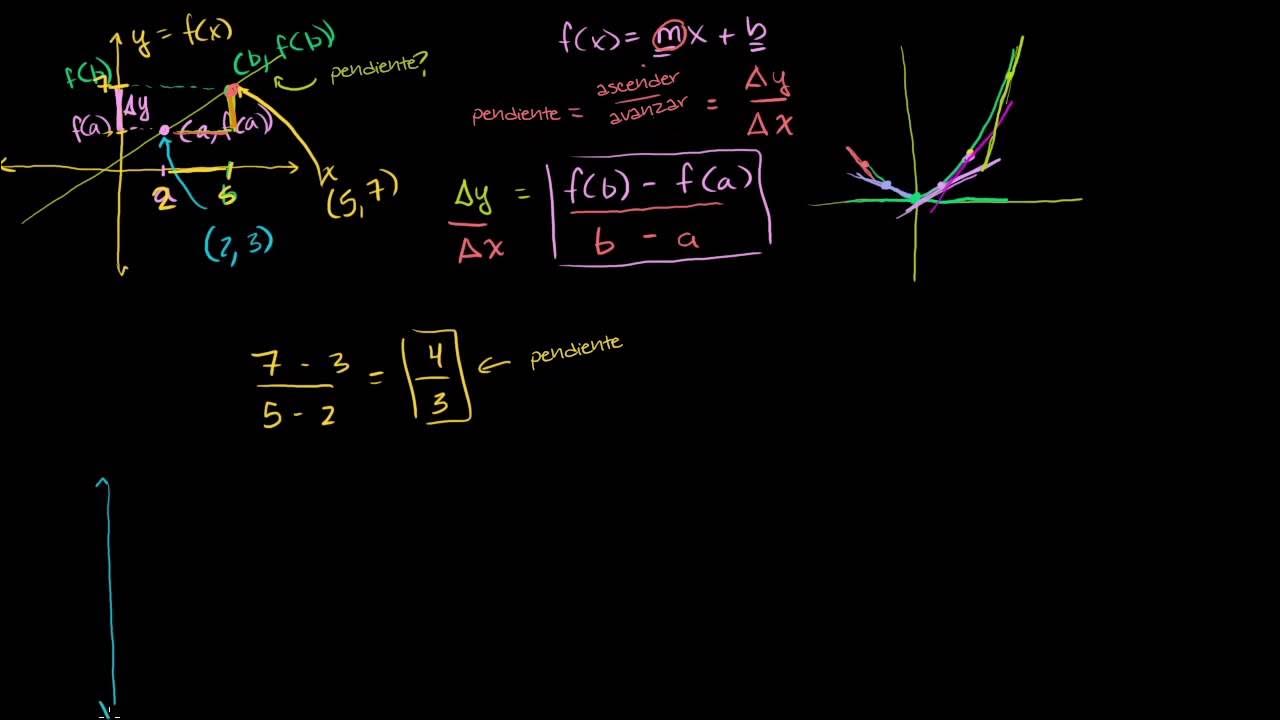
- 🧮 Previously, the gradient was estimated by drawing tangents, but now we can calculate it exactly using derivatives.
- 📐 The derivative is based on the idea of a chord getting shorter as a point approaches another point on the curve.
- 📊 As the distance between the points approaches zero, we get an exact value for the gradient.
- 🔢 The gradient at any point is calculated by finding the limit as the difference in x-values (denoted by h) approaches zero.
- ✏️ The notation f'(x) is used to represent the derivative, or the gradient function.
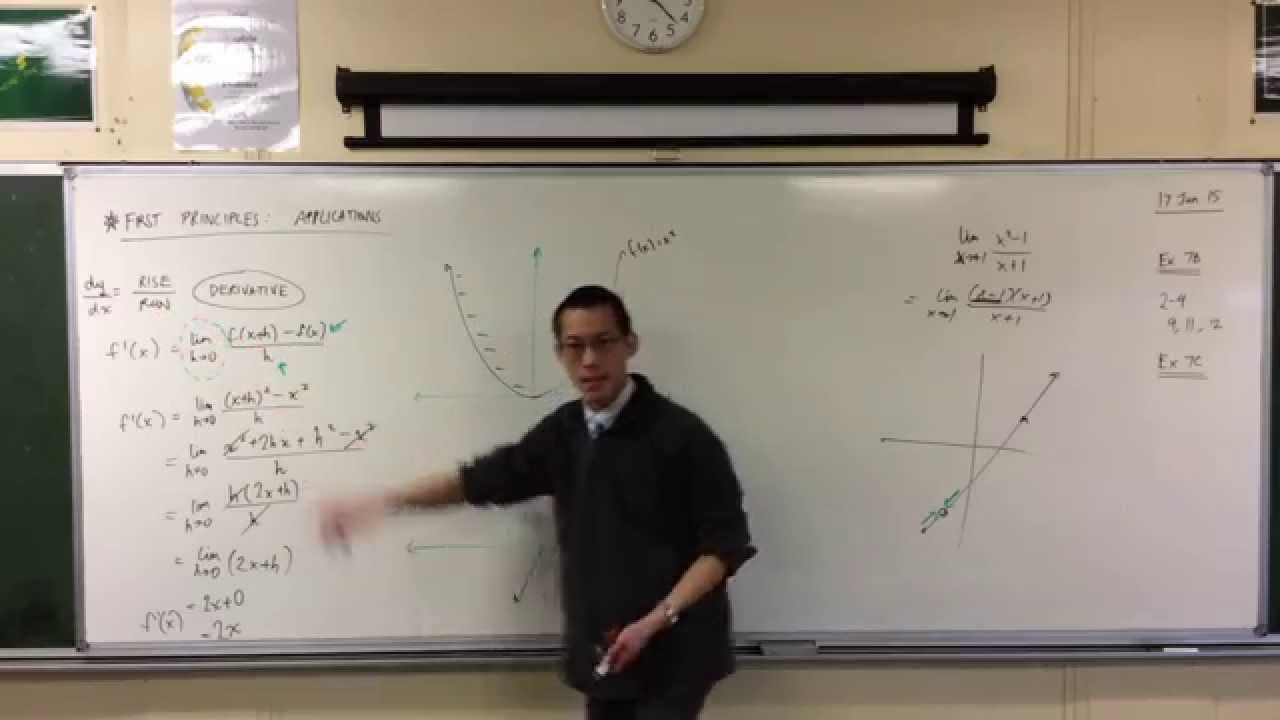
- 📝 To calculate a derivative from first principles, the formula is: f'(x) = limit (h → 0) [f(x+h) - f(x)] / h.
- 🧑🏫 In an example using y = x², the gradient at x = 4 is calculated to be 8 using the derivative formula.
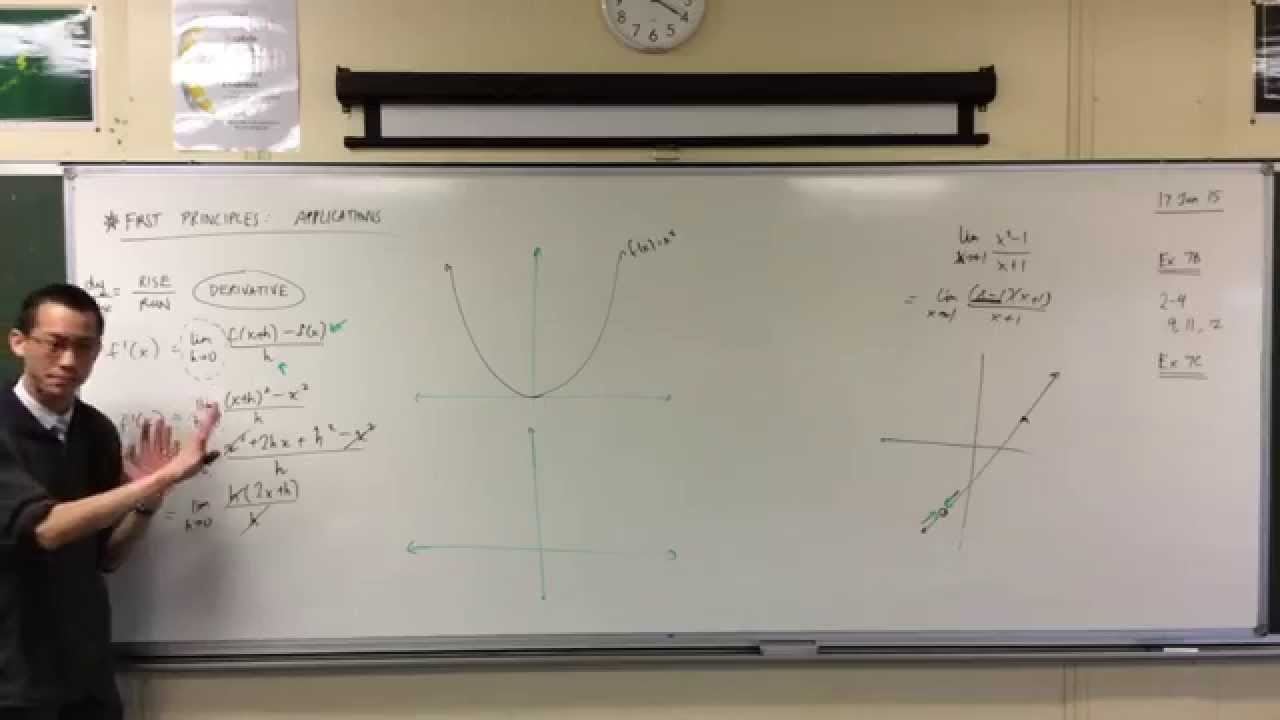
- 🔄 The process of calculating derivatives from first principles allows us to find the gradient for any function.
- 📘 The final example proves that the derivative of x³ is 3x², showing the step-by-step expansion and simplification of the formula.
Q & A
What is the definition of a derivative?
-The derivative is a function that gives the exact value of the gradient at any point on a curve. It allows us to calculate the slope of the tangent line at a specific point without needing to estimate or draw a tangent.
How does the concept of a chord relate to finding the derivative?
-The derivative is based on the idea of a chord connecting two points on a curve. As the two points get closer, the chord becomes a tangent at the desired point. The process of shortening the distance between these points to approach zero gives the exact gradient, which is the derivative.
What is the mathematical notation for the derivative?
-The derivative is commonly denoted as f'(x), read as 'f dash of x.' It represents the gradient function, which gives the slope of the curve at any x-value.
What does the limit notation mean in the context of derivatives?
-The limit notation expresses how the derivative is calculated as the gap (h) between two x-values approaches zero. The derivative is the limit of the difference quotient as h tends to zero, without allowing h to actually become zero, which would make the calculation invalid.
How is the difference quotient related to the derivative?
-The difference quotient is the expression used to find the gradient of a curve at a particular point. It is calculated as (f(x+h) - f(x)) / h, and as h tends towards zero, this gives the derivative, or the exact slope at a point.
What is meant by differentiating from first principles?
-Differentiating from first principles refers to the process of calculating the derivative using the basic definition: the limit of the difference quotient as h approaches zero. This method is foundational in calculus and allows us to derive the gradient function for any given curve.
What is the result of differentiating the function y = x² at the point (4, 16)?
-At the point (4, 16), the gradient of the curve y = x² is 8. This is calculated by applying the limit definition of the derivative to the function at x = 4.
How do you use the first principles method to differentiate a function like y = x³?
-To differentiate y = x³ from first principles, we use the formula for the derivative: the limit as h tends to zero of (f(x+h) - f(x)) / h. Expanding the expression for f(x+h) as (x+h)³ and simplifying, we get the result 3x², which is the derivative of x³.
Why does the h term disappear when h tends to zero in the derivative calculation?
-As h becomes very small and approaches zero, any term containing h (like h² or h) also becomes very small and can be ignored in the final calculation. This leaves only the remaining terms, which give the exact derivative.
What does the derivative 3x² of the function x³ tell us about the graph of x³?
-The derivative 3x² provides the gradient of the graph y = x³ at any point. By substituting a specific x-value into this derivative, we can find the slope of the tangent line at that point on the curve.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
5.0 / 5 (0 votes)