Applying First Principles to x² (1 of 2: Finding the Derivative)

Summary

The video script explains the concept of a derivative in calculus, focusing on how the gradient of a curve changes and cannot be represented by a single constant. It introduces the gradient as a function, leading to the concept of the derivative, which is a function itself. The script discusses the process of finding the derivative from first principles using the limit of the difference quotient. The explanation emphasizes understanding the concept rather than rote memorization and applies it to a specific example involving the function f(x) = x².

Takeaways

• 📚 The concept of 'rise over run' is revisited in the context of a curve where the gradient is not constant but changes, leading to the idea of a gradient function.
• 🔍 The term 'derivative' is introduced as the rate of change of a function, symbolized as f'(x) or \( \frac{dy}{dx} \), which represents the gradient function.
• 📈 The process of finding the derivative involves taking the limit of the rise over run as the run approaches zero, which is the definition of the derivative.
• 👉 The notation f'(x) is used when the function is named 'f', while \( \frac{dy}{dx} \) is used in more general contexts without a specific function name.
• 🚫 Memorizing the process without understanding is discouraged; the importance of grasping the underlying concepts is emphasized.
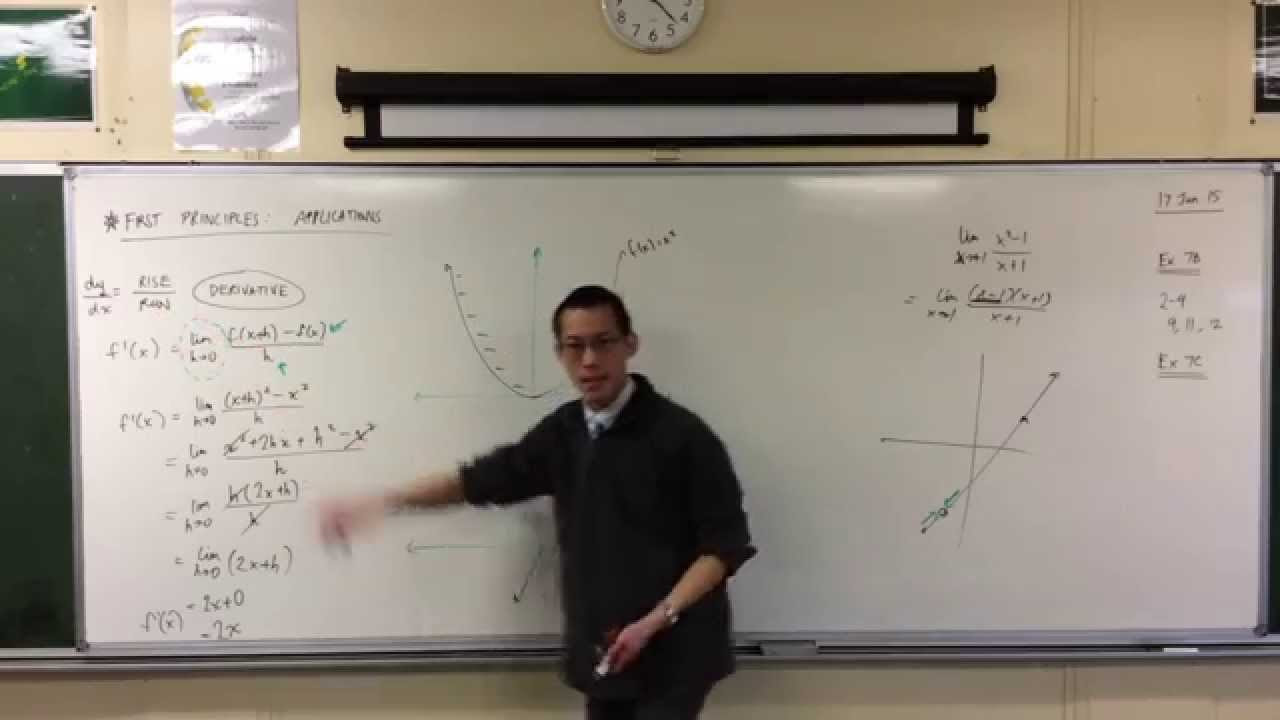
• 🔑 The derivative is calculated by finding the limit as \( h \) approaches zero in the expression \( \frac{f(x+h) - f(x)}{h} \).
• 📉 The example of the parabola f(x) = x^2 is used to demonstrate the process of finding the derivative from first principles.
• 🔄 The process involves algebraic manipulation to simplify the expression and isolate the variable \( h \) to cancel it out before taking the limit.
• 🚫 The limit cannot be taken at \( h = 0 \) directly due to division by zero, but the behavior as \( h \) approaches zero is considered.
• 📌 The derivative of f(x) = x^2 is found to be 2x, which represents the slope of the tangent line to the curve at any point.
• 🔍 The concept of a 'hole' in the derivative function at x = -1 is discussed, indicating a point where the derivative does not exist.

Q & A

What is the concept of 'rise over run' in the context of a curve with changing gradient?

In the context of a curve with a changing gradient, 'rise over run' is not a constant but a function itself. It represents the change in y (rise) over the change in x (run), and is expressed as dy/dx, which is the gradient function of the curve.

Why can't we use the term 'gradient' in the traditional sense for a curve with a variable slope?

We can't use the term 'gradient' in the traditional sense because for a curve with a variable slope, the gradient is not a constant value; it changes at every point on the curve, hence it is better described as a gradient function.

What is the term used to describe the gradient of a function?

The term used to describe the gradient of a function is 'derivative'. It signifies that the gradient is derived from the original function and is itself a function.

How is the derivative of a function represented mathematically?

The derivative of a function is represented mathematically as f'(x), which is another way of indicating the notation for the gradient function of f(x).

What is the significance of the limit as h approaches zero in the context of derivatives?

The limit as h approaches zero is used to find the derivative of a function at a specific point. It helps in transitioning from the concept of the gradient between two points (secant) to the gradient at a single point (tangent).

Why is it important to understand the origin of mathematical concepts like derivatives?

Understanding the origin of mathematical concepts like derivatives is crucial for true comprehension. It prevents mere memorization without grasping the underlying principles, which is essential for applying these concepts effectively.

What is the difference between the gradient of a tangent and the gradient of a secant?

The gradient of a tangent is the instantaneous rate of change at a specific point on a curve, while the gradient of a secant is the average rate of change between two points on the curve. The limit as h approaches zero is used to find the tangent's gradient, which is the derivative.

What is the process of finding the derivative of a function from first principles?

The process involves taking the limit of the difference quotient (f(x+h) - f(x)) / h as h approaches zero. This manipulation helps in isolating h and finding the derivative at a particular point on the function.

Can you provide an example of finding the derivative of a simple function, like f(x) = x^2?

Yes, for f(x) = x^2, the derivative f'(x) is found by taking the limit as h approaches zero of (x+h)^2 - x^2 / h, which simplifies to 2x after canceling out terms and applying the limit.

Why is there a hole in the graph of the function (x^2 - x^2) / h as h approaches zero?

There is a hole at x = -1 because when h approaches zero, the expression (x+h)^2 - x^2 simplifies to 2x + h, and when x = -1, the term 2x + h becomes zero, leading to division by zero, which is undefined.

How does the concept of limits help in understanding the behavior of a function at a point where direct calculation is not possible?

The concept of limits allows us to understand the behavior of a function as it approaches a certain point, even when direct calculation is not possible due to division by zero or other undefined operations. It provides a meaningful result by showing the trend or value the function is approaching.

Outlines

00:00

📚 Introduction to the Derivative Concept

This paragraph introduces the concept of the derivative in calculus, emphasizing the shift from thinking of the gradient as a constant to recognizing it as a variable function. It explains the notation \( \frac{d y}{d x} \) as representing the change in y over the change in x, and introduces the derivative as the gradient function. The paragraph also discusses the first principles approach to finding the derivative, using the limit as \( h \) approaches zero to differentiate between the tangent and secant lines. The importance of understanding the conceptual basis of derivatives rather than just memorizing formulas is highlighted.

05:01

🔍 Calculating the Derivative of a Parabola

The second paragraph delves into the process of calculating the derivative of the function \( f(x) = x^2 \) from first principles. It begins by setting up the limit notation and substituting the function into the derivative formula. The paragraph then walks through the algebraic manipulation required to simplify the expression, including factoring out a common \( h \) and canceling terms to isolate the variable. The discussion touches on the significance of the limit as \( h \) approaches zero and the conceptual understanding of approaching a value without actually reaching it, which is key to grasping the derivative's meaning. The final result of the derivative for \( f(x) = x^2 \) is \( 2x \), which is derived by recognizing the pattern in the simplified expression and applying the limit concept.

Keywords

💡Rise over run

The term 'rise over run' is a basic concept in understanding the gradient of a line, which is the ratio of the vertical change (rise) to the horizontal change (run) between two points. In the context of the video, it is used as a mnemonic to introduce the idea of a gradient, but the script emphasizes that for a curve, the gradient is not constant and thus becomes a function itself, leading to the concept of the derivative.

💡Gradient function

A 'gradient function' is introduced in the video as a way to describe the changing slope of a curve. Unlike a straight line where the gradient is a constant value, a curve's gradient varies at different points. The gradient function is denoted by 'dy/dx' and represents the rate of change of one variable with respect to another.

💡Derivative

The 'derivative' is a fundamental concept in calculus that represents the rate at which a function is changing at a given point. The video explains that the derivative is not just the gradient, but specifically the gradient of the tangent line to the curve at a particular point, which is found by taking the limit as the change in x (h) approaches zero.

💡Limit

The 'limit' is a concept used in calculus to describe the value that a function or sequence approaches as the input approaches some value. In the script, the limit is used to define the derivative, specifically as h (the change in x) approaches zero, which helps in finding the instantaneous rate of change at a point on the curve.

💡First principles

In the context of the video, 'first principles' refers to the foundational method of deriving the derivative of a function by directly applying the limit process to the definition of the gradient. This approach is contrasted with memorization, emphasizing the importance of understanding the underlying process rather than just the formula.

💡Secant

The 'secant' line is mentioned in the video as the line that passes through two points on a curve. It is contrasted with the tangent line, which touches the curve at exactly one point. The script explains that without taking the limit as h approaches zero, the result would be the gradient of the secant line, not the desired tangent line.

💡Tangent

The 'tangent' line is a critical concept in the video, representing the line that touches a curve at a single point and has the same slope as the curve at that point. The derivative of a function at a given point is the slope of the tangent line to the graph of the function at that point.

💡Parabolas

A 'parabola' is a type of curve that is used in the video as an example to illustrate the process of finding the derivative. The script specifically uses the function f(x) = x^2 to demonstrate how to calculate the derivative using the first principles method.

💡Factorization

In the video, 'factorization' is a mathematical technique used to simplify expressions by expressing them as a product of simpler terms. The script demonstrates factorization in the process of finding the derivative of f(x) = x^2, where the expression is factored to isolate h and simplify the limit as h approaches zero.

💡Instantaneous rate of change

The 'instantaneous rate of change' is the concept of how quickly a quantity is changing at a specific moment, which is what the derivative represents. The video script explains that the derivative, found by taking the limit as h approaches zero, gives the instantaneous rate of change at a particular point on a curve.

Highlights

Introduction of the concept of gradient as a function, not a constant, in the context of a curve with changing slope.

Explanation of the notation d/dx for the derivative, representing the change in y over the change in x.

Clarification on the term 'derivative' as it relates to the gradient function derived from the original function.

Emphasis on understanding the origin of mathematical concepts rather than just memorizing them.

Discussion on the difference between the gradient of the tangent and the secant, highlighting the importance of the limit as h approaches zero.

Illustration of the process to find the derivative of a function from first principles, using the limit definition.

Demonstration of the derivative calculation for a simple function f(x) = x^2, emphasizing the steps and rationale.

The significance of the common factor of h in the numerator for simplifying the derivative expression.

Explanation of why h cannot be zero in the derivative calculation and the concept of approaching a limit.

The final simplification of the derivative of f(x) = x^2 to 2x, showcasing the result of the limit process.

Introduction of the concept of a hole in the derivative function at x = -1 due to the division by zero.

Discussion on the practical implications of a hole in the derivative function and its mathematical significance.

The importance of recognizing the approach to a limit even when the exact value cannot be calculated.

Reinforcement of the conceptual understanding of the tangent versus the secant in the context of derivatives.

The final expression of the derivative as 2x, highlighting the outcome of the limit process and its meaning.

Reflection on the process of deriving the derivative and the importance of understanding each step.

Encouragement for students to internalize the concept of derivatives and their application to functions.

Transcripts

picking up where we left off from

yesterday

what we finished with was thinking about

rise over run

in the specific context where you have a

curve like this and its grain is

changing all the time right so gradient

like we usually with straight lines

corner junction and so on we say oh

gradient

we'll just call it m

right because it's just a number it's

just a constant it's not changing it's

not variable right

but here m is not going to cut it m is

not going to cut because in fact the

gradient is not a number it's not a

constant it is a function itself the

gradient is changing wherever you look

right

so therefore we replace this idea of the

gradient as a

constant with the gradient as a function

in fact we call it the gradient function

right and rather than say rise over run

which is just kind of a nice mnemonic

way of remembering what gradient is we

said rise is really the change d delta

the change in y

and run is really the change in x and

that's where we get this d y over dx

notation from okay

now one word i didn't introduce

yesterday is that we call this thing

not just the gradient right but now that

it's a function it's its own thing we

call it the derivative

and derivative you know it just means it

comes from something else right namely

it comes from the actual function right

we learnt this way of taking this rise

over run and putting on these different

points and comparing it with limits

to what was happening at a particular

point on there okay so this is the

introduction the

actual thing that we said was first

principles right we said f dash which is

just yet another way of indicating the

notation right is equal to

the limit

as h approaches zero of now what was our

numerator what was it

f of x plus h f of x plus h right and

then we take away

f of x now just remember why do we do

that it's because if x plus h is here

and f of x is here and we just want the

difference that's all it is that's the

rise and of course there's the run

do you remember when i said to you we're

introducing this topic the worst thing

that you can do is just get get to work

memorizing stuff and not know where it

comes from um

i remember sitting next to you when i

was in year 11 sitting next to people

who just like look it's just just

memorize it okay doesn't matter what any

of it means okay

that's the quickest way to get on the

path of not actually understanding

what's happening

this is rise

right

this is run

one last thing what difference

does that make if it weren't there that

limit as h approaches zero if it weren't

there it's not meaningless but what

would it be it'd be something else yeah

it'll be the gradient of

not that not the tangent the tangent is

what we want right but if you've got two

points that are actually a part it'll be

the secant wouldn't right it's not

meaningless that's how we started it's

just not what we want this is the

gradient of the tangent the derivative

without that and many people like i have

to write this over and over again

without that it's the gradient of the

second we're not after that

okay so now that's where we stopped

right now we want to apply it to a

particular situation okay so here's a

function right now the one we'll start

with the easiest one to start with is

just the parabola x squared okay

if you see f of x right then you can use

this f dash x notation okay if on the

other hand

all you see is this

there is no function called f right so

none of this really makes sense f dash

what is any of that in here you would

have to use this notation up here right

if you've got y's you'd use d y and d x

if you've got f's you'd use

f and f dash okay

now i'm just going to come back because

for this example we're just starting off

i do actually want to go with um f

because i'll make this a bit easier so

this is f of x equals x squared

okay

let's proceed through this right if f of

x is that

then f dash x

is going to equal 2. now

it begins with just the substitution if

we know what f is i should know what all

those pieces are in there okay so

we begin with the limit

because i'm interested in the tangent

and not the secant

if f of x is x squared

then f of

x plus h

is x plus h all squared you agree with

that

and there's f of x just as we defined it

we're dividing through by h okay now

what we're about to do is what we call

evaluating the derivative evaluating the

derivative from first principles this is

our starting point okay

what we're trying to do is manipulate

this in such a way such that i can

actually put h equals 0 in there and see

what happens i can't do that right now

because h is on the denominator you

divide by zero it explodes okay so i

want to reshape this into something

that gets rid of h being just by itself

on the denominator okay so let's give

this a go obviously you look at the

numerator that's the only thing you can

do anything with here the numerator the

denominator is just simplified so i

write my limit

because i want the tangent not the

secant you're going to get really sick

of me saying that but i want you to get

in your head it's really important to

keep on saying it

on the numerator perfect square when you

expand it you get

x squared plus

2hx plus h squared and then there's that

minus x squared attacking along the end

okay and then of course everything is

divided by h right just because you're

not doing any work with them don't

forget to write this or the denominator

they're still there and they're still

critically important

having expanded you can see i can do

something with this now can't i got an x

squared on the front minus x squared on

the back

and they're going to cancel each other

out okay

now the reason why this is good is

because now i have a common factor of h

on the numerator right common factor

ratio let me take it out let me

factorize it

limit as h approaches 0 because i want

the tangent not the secant

of what's on the numerator

h outside of

2x

plus h good there's still there's still

an h hanging around there that's all

divided through by h okay

fantastic now i can cancel

denominator's gone

yep isn't that like the equivalent of

dividing like

by like like

canceling out

yes this is exactly right i'm glad you

raised that point why can i get rid of

this okay

let me pull back to you if you're here

like this um

this okay now what does this thing look

like okay uh

sorry yes

yes thank you

okay

now i was on autopilot for a second um

what does this thing look like even

though it's got next squared on the top

because of what you get on the bottom

you're actually going to get a straight

line aren't you okay when you factorize

x approaches negative one

um x minus one

so what does this thing actually look

like it looks like this straight line

with one difference namely

there's a hole there there's just a hole

right so

uh x minus one what does that look like

down here

and x equals negative one somewhere over

here i guess

there's my little hole there okay so our

problem is i can't simply input x equals

negative one because then as you notice

i'm i'm multiplying by zero and dividing

by zero and it loses meaning okay

however what i'm just come back to when

we define this idea of our limit right

what i'm trying to think about is what

am i

getting

towards

right and i am actually getting towards

something real even though i can't be

there itself any more than i can

calculate the gradient of you know a

point to itself that's what this is

really doing rise over run as the two

points get close together right

i can't actually calculate that but i

can still see what it's approaching and

if it's approaching the same thing from

both angles then that's fine that's

great i can take that as a meaningful

result okay

so though a very good point to mention

because it's like yeah why can't i do

that and the answer is because h can't

be actually equal to zero so i can take

it out of the equation

expression i should say now that i've

done this

this is the last time i'm going to write

the limit as h approaches zero because i

want say it with me

the tangent

not the secret right

just like a hammer anywhere okay so now

that i'm there

i've gotten rid of h on the denominator

all right

by the way h can be on the denominator

just not by itself because when it's by

itself the denominator becomes zero as

you'll see shortly

now i actually can't say well let's just

see what happens when h is zero and the

answer is it's two x plus zero don't

miss the plus zero it's not trivial okay

just like

multiplying by one sometimes is not

trivial adding zero is not trivial

because i see it comes from here and

that of course is just 2x okay

what's mean