y=mx+b Ecuacíon de la recta, relación funcional
Summary
TLDREn este video, el profesor Toño explica de manera didáctica el origen y la importancia de la ecuación de la recta (y = mx + b). Utiliza ejemplos cotidianos, como el flujo de agua en un tanque, para demostrar cómo las matemáticas y el álgebra se aplican en la vida real. Además, destaca la importancia de la modelación algebraica y cómo entender la variación lineal. El uso de herramientas como tablas y gráficas ayuda a visualizar cómo se construyen las ecuaciones y su relación con el mundo real, haciendo énfasis en conceptos clave como la pendiente y la ordenada al origen.
Takeaways
- 📚 El video aborda el tema de la ecuación de la recta, específicamente la fórmula y = mx + b, y se enfoca en explicar su origen y cómo se llega a esa expresión.
- 🔍 El objetivo principal es enseñar a los estudiantes a modelar situaciones cotidianas usando expresiones algebraicas, facilitando así su comprensión del álgebra.
- 💧 Un ejemplo cotidiano utilizado es la cantidad de agua que cae de una llave por minuto y cómo modelar esta situación mediante una ecuación lineal.
- 🔢 La modelación se realiza traduciendo un problema de la vida real (litros por minuto) al lenguaje algebraico, asignando variables como 'x' para minutos y valores numéricos para la cantidad de agua.
- 📊 Se construye una tabla de valores consecutivos para 'x' (minutos) y se muestra cómo el valor de 'y' (litros) varía en función de 'x'.
- 📈 La pendiente (m) de la ecuación representa la tasa de cambio, en este caso, los litros que caen por minuto, mientras que el término independiente (b) representa el valor inicial (litros ya presentes en el tanque).
- 📏 Se introduce el concepto de variación lineal, que indica cómo la relación entre dos variables forma una línea recta en el plano.
- 🧠 El video explica que la ecuación de la recta tiene una forma estándar (y = mx + b), donde 'm' indica la pendiente y 'b' es el punto de intersección con el eje Y.
- 💡 También se enfatiza la importancia de entender la inclinación de la recta, que depende del valor de la pendiente, y cómo afecta el comportamiento de la ecuación.
- 🎓 Se utiliza la aplicación GeoGebra para visualizar el comportamiento de diferentes ecuaciones lineales y ayudar a los estudiantes a deducir conceptos clave como pendiente, intersección y variación proporcional.
Q & A
¿Cuál es el propósito del video mencionado en el guion?
-El propósito del video es explicar el origen de la ecuación de la recta y cómo se llegó a su forma, así como mostrar cómo modelar situaciones reales utilizando expresiones algebraicas.
¿Qué problema común enfrentan los estudiantes al aprender álgebra según el profesor?
-El problema común es que los estudiantes no saben articular las matemáticas en la vida cotidiana, lo cual hace difícil comprender el álgebra y la modelación de expresiones algebraicas.
¿Qué es la modelación en el contexto de matemáticas, según el profesor?
-La modelación es la traducción del lenguaje natural a una expresión algebraica, permitiendo representar situaciones reales con ecuaciones matemáticas.
¿Qué situación real usa el profesor para explicar la ecuación de la recta?
-El profesor usa la situación de un tanque de agua al que le caen tres litros por minuto para explicar cómo modelar la variación lineal y llegar a la ecuación de la recta.
¿Qué significa que la ecuación sea una variación lineal?
-Una variación lineal significa que una cantidad (como los litros de agua) aumenta de forma proporcional al tiempo, generando una relación que puede ser representada gráficamente como una línea recta.
¿Qué papel tiene la constante en la ecuación de la recta?
-La constante en la ecuación de la recta (m) representa el coeficiente de la variable x, indicando la tasa de cambio o pendiente, que en el ejemplo es la cantidad de litros que caen por minuto.
¿Qué significa el término 'pendiente' en la ecuación de la recta?
-La pendiente es el coeficiente de la variable x y determina qué tan inclinada está la recta en el plano, indicando la razón de cambio entre dos variables.
¿Qué representa la ordenada al origen (b) en la ecuación de la recta?
-La ordenada al origen (b) en la ecuación de la recta indica el punto donde la recta intercepta el eje de las y, es decir, el valor inicial o el desplazamiento vertical de la línea.
¿Cómo se puede visualizar la ecuación de la recta utilizando Geogebra?
-En Geogebra se puede visualizar la ecuación de la recta como una línea que representa la relación entre las variables. Dependiendo de los valores de la pendiente y la ordenada, la línea tendrá una inclinación y un punto de intersección diferente.
¿Qué diferencia hay entre una recta con pendiente mayor y otra con pendiente menor?
-Una recta con pendiente mayor estará más inclinada hacia arriba, mientras que una recta con pendiente menor será menos inclinada. Esto indica que la tasa de cambio es mayor en la primera que en la segunda.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Ex 6: Conic Section: Parabola with Horizontal Axis and Vertex NOT at the Origin (Right)

21. Encontrar la pendiente de una recta dada la ecuación general

Ecuaciones de la recta y sus transformaciones

Introducción a la ecuación de la recta, fundamentos
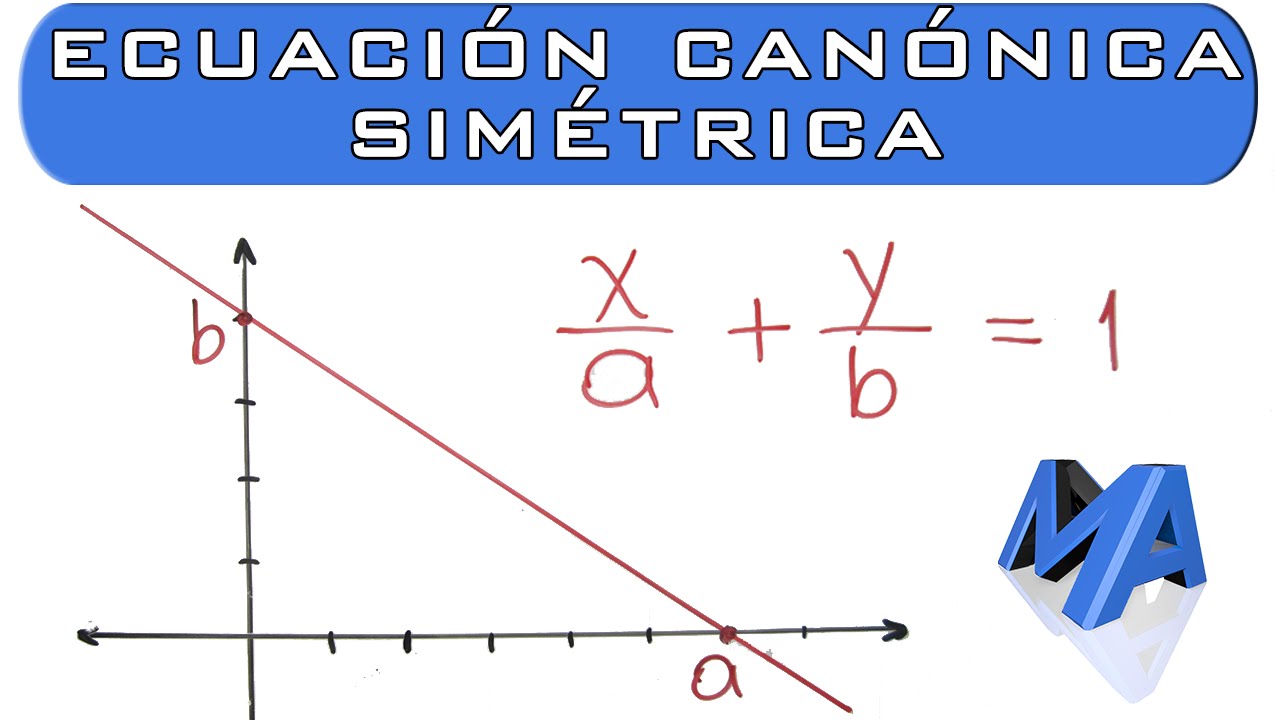
Ecuación canónica o simétrica de la recta

Distancia entre dos puntos Ejemplo 1
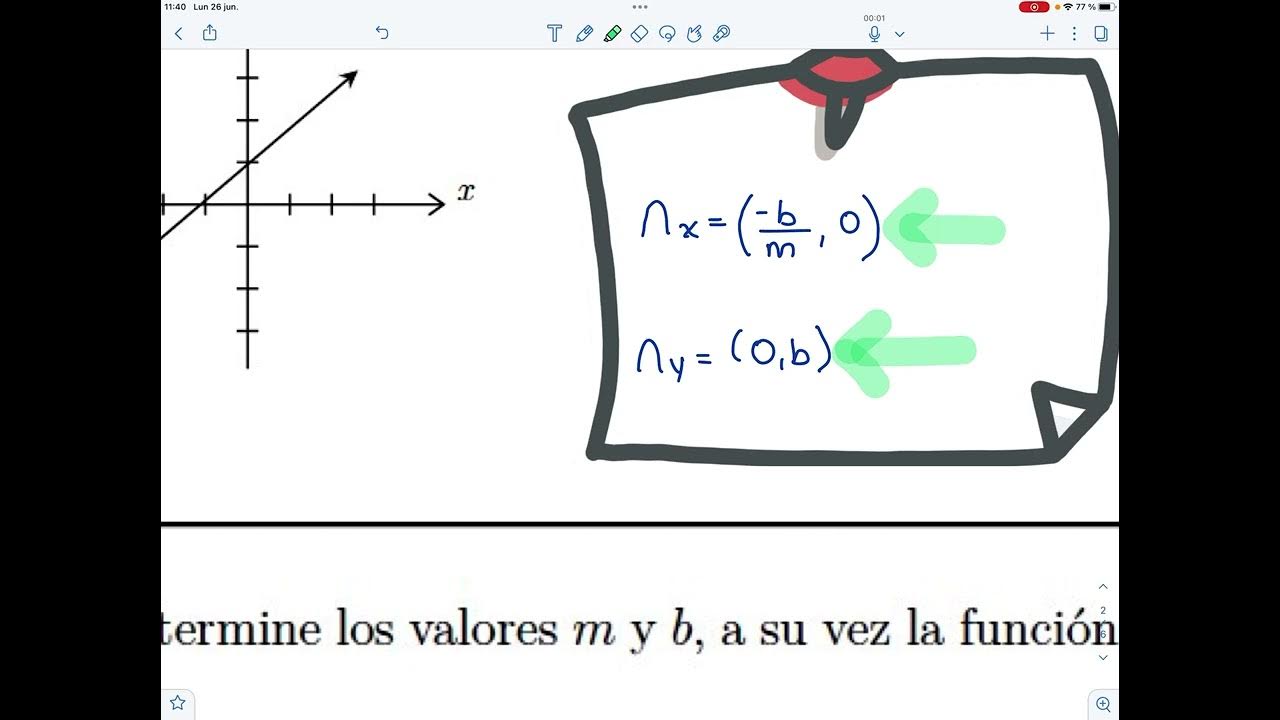
1 Funcion lineal
5.0 / 5 (0 votes)