How To Solve Projectile Motion Problems In Physics
Summary
TLDRThis video provides an in-depth explanation of projectile motion, focusing on key concepts like kinematic equations, constant speed, and acceleration. It covers the fundamental equations for displacement, velocity, and time, emphasizing the relationship between horizontal and vertical velocities in projectile motion. The instructor explains different types of trajectories, such as horizontal motion off a cliff and motion at an angle, highlighting important equations for calculating time, height, and range. The video also demonstrates solving example problems to apply these concepts, making it a comprehensive resource for understanding projectile motion in physics.
Takeaways
- 🚀 The kinematic equations at constant speed include displacement (d) = velocity (v) multiplied by time (t), and at constant acceleration, displacement equals average velocity times time.
- ⚡ Average velocity under constant acceleration is the sum of initial and final velocity, divided by two.
- 🎯 Key equations: final velocity (v final) = initial velocity (v initial) + acceleration (a) × time (t), and final velocity squared = initial velocity squared + 2 × acceleration × displacement.
- 🌍 Gravitational acceleration is approximated as -9.8 m/s², and in the example, it's rounded to -10 m/s² for simplicity.
- ⚖ Horizontal velocity (vx) remains constant in projectile motion, while vertical velocity (vy) changes due to gravitational acceleration.
- 💡 In a projectile, only gravity acts on the object after release; horizontal acceleration is zero, and vertical acceleration is constant.
- 🔄 The speed at the same height on both sides of the projectile’s arc is the same, but vertical velocity changes in direction (positive on the way up, negative on the way down).
- 📏 Three common projectile trajectories: (1) horizontal motion off a cliff, (2) motion starting from the ground going up and coming down, and (3) motion from a height kicked at an angle.
- 📐 The range (horizontal distance) in projectile motion can be calculated using v_x × time, while the height or vertical displacement follows the equation y_final = y_initial + v_initial × time + 1/2 × acceleration × time².
- 🧮 To find the final speed before an object hits the ground, use the Pythagorean theorem: v = sqrt(vx² + vy²).
Q & A
What are the basic kinematic equations under constant speed?
-Under constant speed, displacement (d) is equal to velocity (v) multiplied by time (t): d = vt.
How do you calculate displacement under constant acceleration?
-Displacement is equal to the average velocity multiplied by time. Average velocity is the sum of the initial and final velocity, divided by two.
What is the formula for final velocity under constant acceleration?
-The final velocity (v_final) is equal to the initial velocity (v_initial) plus the acceleration (a) multiplied by time (t): v_final = v_initial + at.
How do you calculate the displacement if the acceleration is constant?
-The displacement (d) can be calculated using the formula: d = v_initial * t + 0.5 * a * t^2.
What happens to the horizontal and vertical velocities of a projectile one second after launch?
-The horizontal velocity remains constant, while the vertical velocity decreases by 10 m/s due to gravitational acceleration (assuming g = 10 m/s² for simplicity).
Why does the vertical velocity change but the horizontal velocity stays the same in projectile motion?
-The vertical velocity changes due to gravitational acceleration acting in the vertical direction, while the horizontal velocity remains constant because there is no acceleration in the horizontal direction (neglecting air resistance).
How does speed differ from velocity?
-Speed is the magnitude of velocity and is always positive. Velocity is a vector, meaning it has both magnitude and direction, and can be positive or negative depending on direction.
What is the formula to calculate the time for a projectile to reach its maximum height?
-The time to reach maximum height is calculated using the formula: t = (v * sin(θ)) / g, where v is the initial speed, θ is the angle of projection, and g is the acceleration due to gravity.
How can you calculate the range of a projectile?
-The range of a projectile can be calculated using the formula: Range = (v² * sin(2θ)) / g, where v is the initial speed, θ is the angle of projection, and g is the acceleration due to gravity.
How do you find the final speed of a projectile before it hits the ground?
-The final speed (v) before hitting the ground can be calculated using the Pythagorean theorem: v = sqrt(v_x² + v_y²), where v_x is the constant horizontal velocity and v_y is the vertical velocity at the final moment.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
AP Physics 1 - Unit 1 Summary - Kinematics

Kinematic Equations in One Dimension | Physics with Professor Matt Anderson | M2-04

Two Dimensional Motion (4 of 4) Horizontal Projection, Worked Example
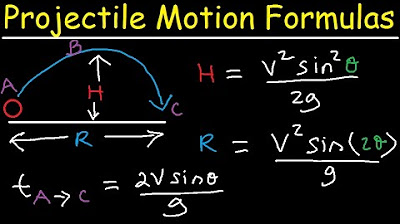
Introduction to Projectile Motion - Formulas and Equations

Movimiento Rectilíneo Uniformemente Acelerado o Variado MRUA MRUV | Ejemplo 2

Projectile Motion: Finding the Maximum Height and the Range
5.0 / 5 (0 votes)
