Graficar Funciones Lineales en 3 pasos (ordenada y pendiente) | Ejemplos
Summary
TLDREste video explica cómo graficar funciones lineales de manera fácil y rápida. Comienza recordando que las funciones lineales tienen una variable independiente de grado uno y un término independiente. Luego, el proceso se ejemplifica con tres funciones diferentes. Se muestran pasos para ubicar los puntos clave en el plano, utilizando el término independiente y el número que acompaña a la variable x, desplazándose en el eje y y en el eje x. También se destaca cómo manejar funciones sin término independiente, y se dan recomendaciones para tratar coeficientes decimales. Es un método práctico para graficar líneas rectas.
Takeaways
- 📊 Las funciones lineales tienen una variable independiente de grado uno y un término independiente.
- 📏 La gráfica de una función lineal es una línea recta, y basta con conocer dos puntos para graficarla.
- 📝 Se puede usar una tabla de valores o puntos de corte con los ejes, pero en este caso se utilizará un método más corto.
- 🟢 En la primera función f(x) = 2/3x + 1, el término independiente es 1 y se ubica en el eje y.
- 🔢 El numerador (2) indica el desplazamiento hacia arriba o abajo, y el denominador (3) indica el desplazamiento hacia la derecha.
- 📐 Después de marcar dos puntos en la gráfica, se unen con una regla para formar la recta.
- 🔴 En la segunda función g(x) = -4x + 2, el término independiente es 2, y se desplaza 4 unidades hacia abajo y 1 unidad a la derecha.
- ⚫ La tercera función y(x) = -5/2x no tiene término independiente, por lo que el primer punto es el origen.
- ⬇️ Se desplazan 5 unidades hacia abajo y 2 hacia la derecha para graficar la tercera función.
- 📎 Si el término independiente es cero, la función pasa por el origen, y es recomendable convertir decimales a fracciones.
Q & A
¿Qué característica principal tienen las funciones lineales?
-Las funciones lineales tienen la variable independiente 'x' de grado uno, es decir, con exponente 1, y un término independiente o un número sin variable.
¿Cómo es la gráfica de una función lineal?
-La gráfica de una función lineal es una línea recta.
¿Qué método se utiliza en el video para graficar una función lineal?
-Se utiliza un procedimiento basado en identificar el término independiente y el número que acompaña a la variable 'x' para ubicar los puntos en el plano y luego trazar la recta.
¿Qué representa el término independiente en una función lineal?
-El término independiente es el número que se ubica en el eje 'y' cuando 'x' es igual a cero.
En la función f(x) = (2/3)x + 1, ¿qué significa el numerador y el denominador del coeficiente 2/3?
-El numerador 2 indica cuántas unidades se desplaza hacia arriba (porque es positivo), y el denominador 3 indica cuántas unidades se desplaza hacia la derecha.
¿Cómo se traza la gráfica de la función f(x) = (2/3)x + 1?
-Primero se ubica el valor 1 en el eje 'y', luego se suben 2 unidades y se desplazan 3 unidades hacia la derecha para marcar el segundo punto. Finalmente, se trazan ambos puntos con una regla.
En la función g(x) = -4x + 2, ¿cómo se interpreta el coeficiente de 'x'?
-El coeficiente -4 indica que se deben bajar 4 unidades (por ser negativo) y luego desplazarse una unidad hacia la derecha.
¿Cómo se grafica la función g(x) = -4x + 2?
-Primero se ubica el 2 en el eje 'y', luego se bajan 4 unidades y se desplaza una unidad hacia la derecha para marcar el segundo punto. Finalmente, se trazan ambos puntos con una regla.
En la función y(x) = (-5/2)x, ¿qué indica que no haya un término independiente?
-Cuando no hay un término independiente, significa que la gráfica pasa por el origen de coordenadas (0,0).
¿Qué se recomienda hacer si el coeficiente de 'x' es un decimal?
-Se recomienda convertir el decimal a fracción y luego aplicar el mismo procedimiento para graficar la función.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Tutorial como crear encuestas en Google Drive Fácil y Rápido 2020

I - ¿Qué es una curva paramétrica? ¿Cómo la graficamos?

GRAFICAR FUNCIONES LINEALES PARTE 3 Super facil - Para principiantes

¿Qué es LA FUNCIÓN LINEAL? l Explicación sencilla l La pendiente l Ejemplos l Gráfica
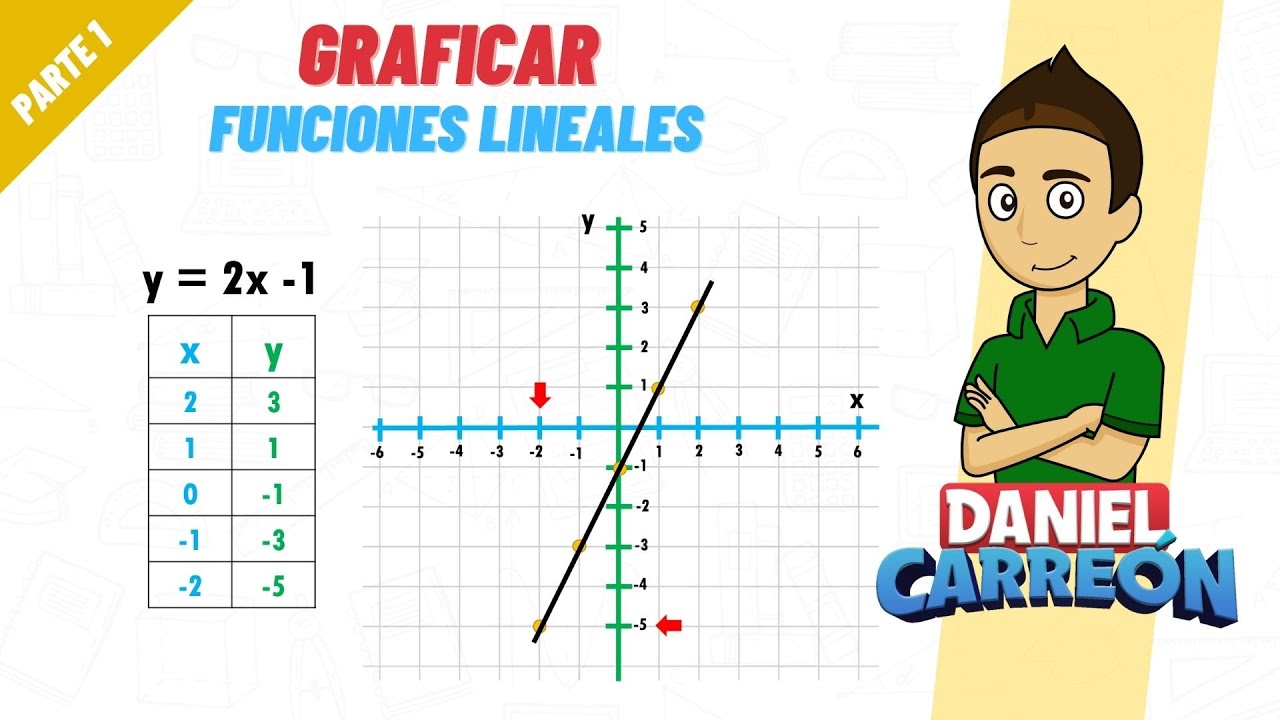
GRAFICAR FUNCIONES LINEALES PARTE 1

Sistemas de ecuaciones | Solución Método Gráfico | Ejemplo 2
5.0 / 5 (0 votes)