Intro to wave superposition
Summary
TLDRThis video explores wave superposition, also known as interference, where overlapping waves create combined effects. It explains how waves add algebraically when they meet, resulting in constructive or destructive interference based on their phase relationship. The video uses interactive simulations to demonstrate these concepts, showing how different waves interact and the mathematical relationships governing their interference patterns.
Takeaways
- 🌊 The concept of wave superposition refers to the overlapping of two waves, which can also be called interference.
- 📐 When two waves meet, their effects add up algebraically, resulting in the combined height of the waves.
- 🔄 If two pulses are identical, their heights add up when they meet; if they differ, their combined height is the sum of their individual heights.
- 🔄 Negative pulses can result in a net effect of zero when they align perfectly, demonstrating destructive interference.
- ⏱ The timing of the wave's movement is crucial as it determines when interference occurs.
- 🌐 Different shaped pulses can interfere, resulting in a pattern that is the sum of the overlapping patterns at any given moment.
- 🌉 Standing waves are a special case of interference where waves travel in opposite directions and create a stationary pattern.
- 🔗 The resultant wave from two interfering waves is the algebraic sum of the two individual waves.
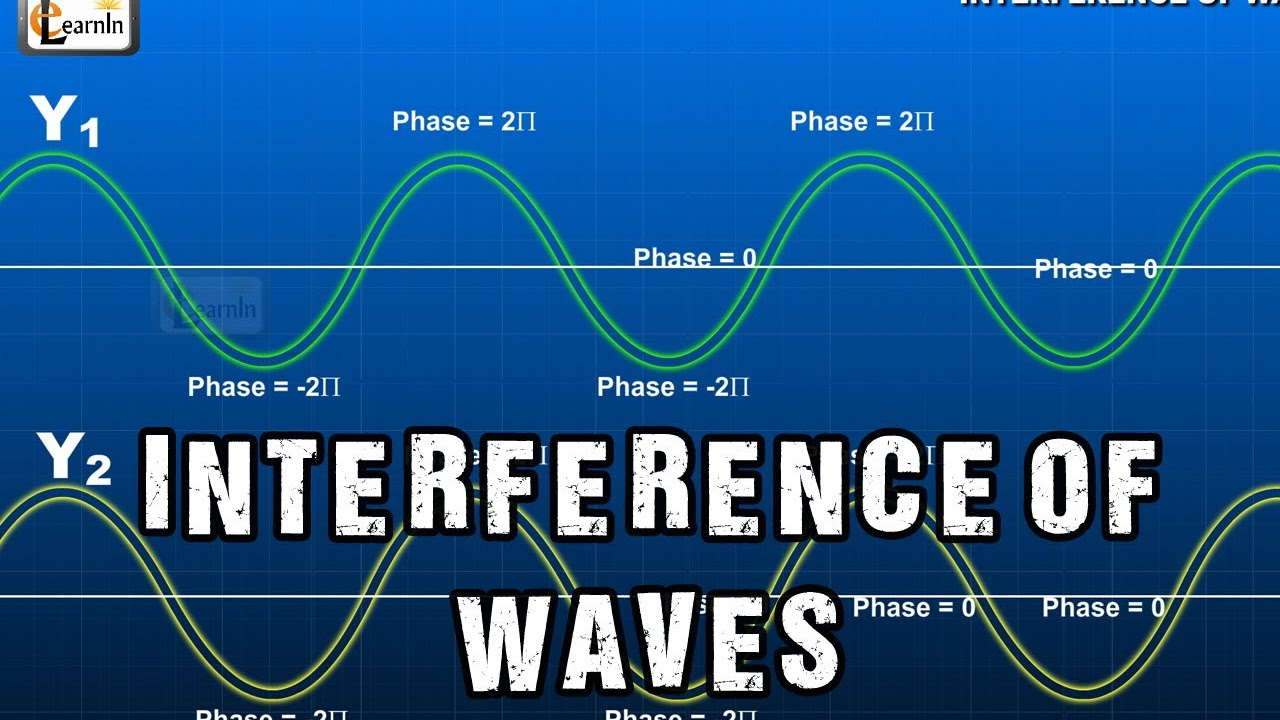
- 📉 The phase difference between two waves is critical in determining whether the interference is constructive or destructive.
- 🔄 Constructive interference occurs when the phase difference is a multiple of 2π, while destructive interference happens when the phase difference is an odd multiple of π.
- 📚 The relationship between phase difference and path difference is given by the equation Δφ = 2π/λ * Δr, where Δφ is the phase difference, Δr is the path difference, and λ is the wavelength.
Q & A
What is meant by 'superposition' in the context of waves?
-Superposition refers to the overlapping of two or more waves in position and time. When this happens, the resulting wave is the algebraic addition of the individual effects of the waves.
What are the two types of interference that occur during superposition?
-The two types of interference are constructive interference, where the waves combine to create a larger amplitude, and destructive interference, where the waves cancel each other out.
What happens when two identical waves meet during constructive interference?
-When two identical waves meet during constructive interference, their amplitudes add together, resulting in a wave with a combined height equal to the sum of their individual heights.
How does destructive interference occur between two waves?
-Destructive interference occurs when two waves meet, and one wave has a positive amplitude while the other has an equal negative amplitude. This causes their effects to cancel each other out, resulting in a net amplitude of zero at that instant.
What is a standing wave, and how is it formed?
-A standing wave is a type of wave that appears to be stationary, formed by the interference of two waves traveling in opposite directions. In a standing wave, certain points (nodes) remain still while others (antinodes) oscillate with maximum amplitude.
What is the significance of phase difference in wave superposition?
-Phase difference refers to the offset between the phases of two waves. It plays a crucial role in determining the type of interference. A phase difference of zero results in constructive interference, while a phase difference of 180° (or π radians) results in destructive interference.
What is the general expression for the superposition of two waves with a phase difference?
-The general expression for the superposition of two waves with a phase difference is given by the equation: 2A * cos(ϕ/2) * sin(Kx - ωt + ϕ/2), where ϕ is the phase difference, K is the wave number, and ω is the angular frequency.
How does the phase difference affect the resultant wave in a simulation of superposition?
-In the simulation, when two waves have a phase difference of zero, they interfere constructively, doubling the amplitude. When they have a phase difference of 180°, they interfere destructively, canceling each other out.
What are the conditions for constructive interference in terms of phase and path difference?
-Constructive interference occurs when the phase difference between two waves is zero or when the path difference is an integer multiple of the wavelength (mλ, where m is an integer).
What are the conditions for destructive interference in terms of phase and path difference?
-Destructive interference occurs when the phase difference is 180° (or π radians) or when the path difference is an odd multiple of half the wavelength ((m + 1/2)λ).
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Wave interference | Mechanical waves and sound | Physics | Khan Academy

A Level Physics Waves Revision: Superposition, phase difference, path difference and interference
Interference of Waves | Superposition and Interference in light and water waves | Physics

Super Position Principle, Interference of Light, Coherent Source, Chapter 10, Wave Optics, Class 12

Interference, Reflection, and Diffraction

[1.5] Interference of waves
5.0 / 5 (0 votes)
