A Level Physics Waves Revision: Superposition, phase difference, path difference and interference

Summary

In this video, the speaker explores key concepts of wave interference, including superposition, phase difference, path difference, and coherence. The principle of superposition is discussed, where the resultant displacement of two waves is the sum of their individual displacements. The video also covers phase differences and how they relate to wave interactions, explaining both constructive and destructive interference. The concept of path difference, along with its mathematical expression and conditions for constructive and destructive interference, is demonstrated through examples like the double-slit experiment. Overall, the video provides a detailed explanation of wave behavior and interference patterns.

Takeaways

• 😀 The principle of superposition states that when two waves interact, the resultant displacement is the vector sum of the individual displacements.
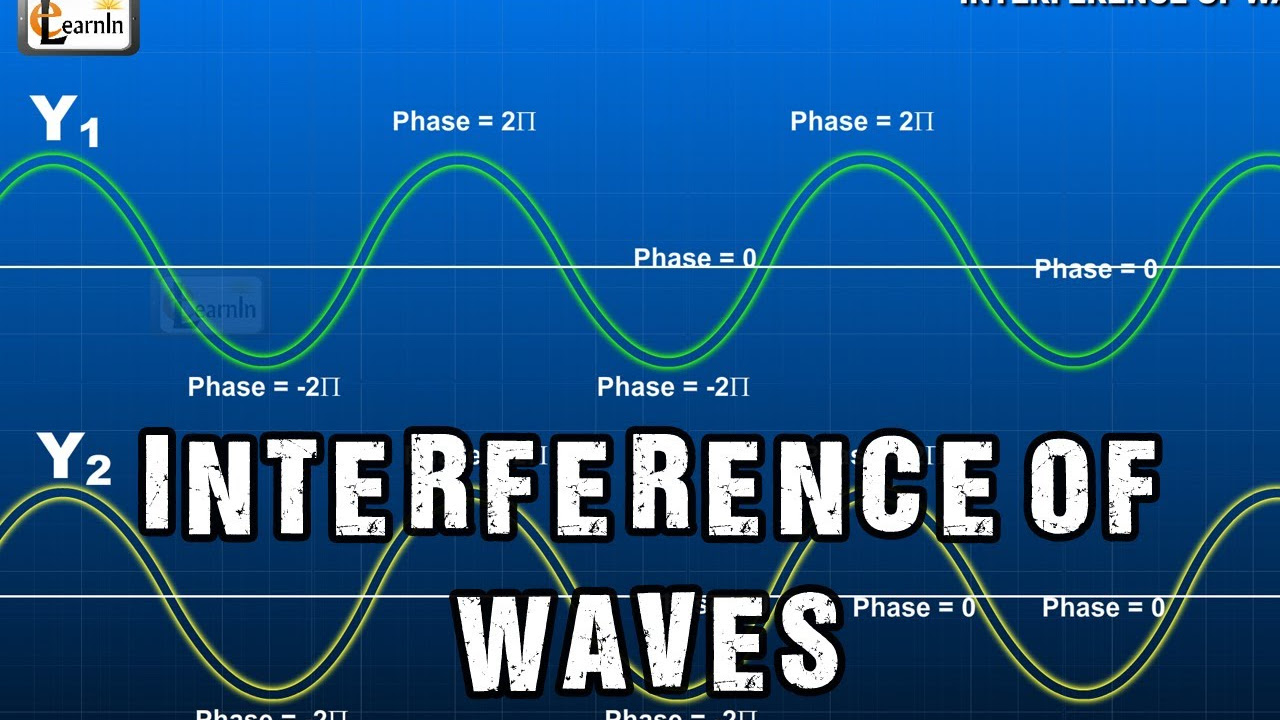
• 😀 Phase difference is a measure of how out-of-sync two waves are, expressed as a fraction of the wavelength times 360 degrees.
• 😀 Coherent waves maintain a constant phase difference, which is essential for analyzing interference patterns.
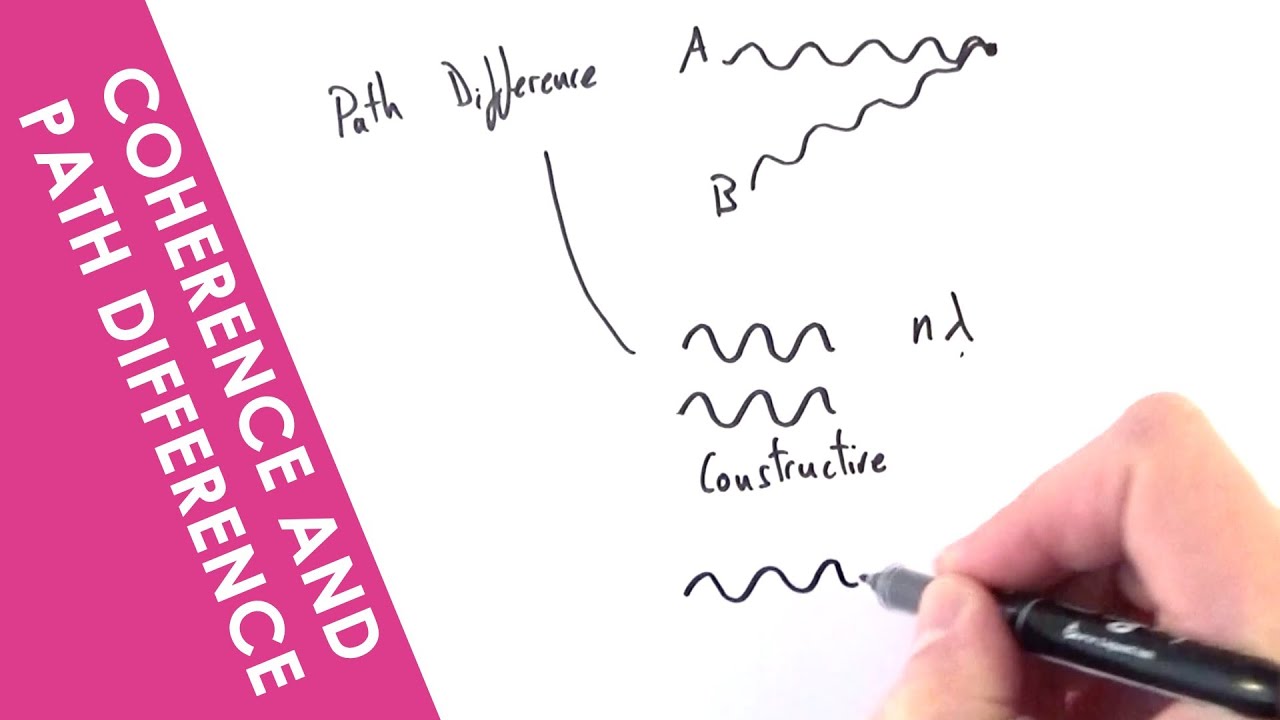
• 😀 In the double-slit experiment, path difference is the difference in distance traveled by two waves to reach a specific point.
• 😀 Constructive interference occurs when the phase difference is 0, 360, or any multiple of 360 degrees, leading to a bright spot.
• 😀 For constructive interference, the path difference must be a multiple of the wavelength.
• 😀 Destructive interference occurs when waves are in antiphase, meaning the peak of one wave meets the trough of another.
• 😀 The path difference for destructive interference must be an odd multiple of half the wavelength (n + 1/2) times the wavelength.
• 😀 A path difference of zero results in constructive interference, while a path difference equal to half the wavelength results in destructive interference.
• 😀 Interference patterns depend on both phase difference and path difference, and these conditions lead to either bright or dark spots on the screen.

Q & A

What does the principle of superposition state?

The principle of superposition states that when two waves interact, the resultant displacement at any point is the vector sum of the individual displacements of the waves at that point.

How do you calculate the resultant displacement of two waves with different amplitudes?

The resultant displacement is the sum of the individual displacements. For example, if one wave has an amplitude of 2 meters and another has an amplitude of 1 meter, the resultant displacement would be 3 meters.

What is phase difference and how is it expressed?

Phase difference refers to how far out of sync two points in a wave or two separate waves are. It is expressed as a fraction of the wavelength times 360 degrees.

What is meant by waves being 'coherent'?

Two waves are coherent if they have a constant phase difference. This means that the phase difference between the waves does not change over time.

What is path difference and how does it relate to interference?

Path difference is the difference in the distance traveled by two waves from their sources to a particular point. It plays a key role in determining whether the waves will interfere constructively or destructively.

What are the conditions for constructive interference?

Constructive interference occurs when the phase difference between the two waves is a multiple of 360 degrees (e.g., 0°, 360°, 720°) and the path difference is a multiple of the wavelength.

How does path difference influence the interference pattern?

The path difference determines whether the waves will meet in phase (constructive interference) or out of phase (destructive interference). A path difference that is a multiple of the wavelength results in constructive interference, while a path difference that is an odd multiple of half the wavelength results in destructive interference.

What is the significance of the wavelength in determining constructive interference?

For constructive interference to occur, the path difference between the waves must be a multiple of the wavelength. For example, if the wavelength is 1 cm, a path difference of 1 cm, 2 cm, or 3 cm will produce constructive interference.

How does destructive interference occur?

Destructive interference occurs when the phase difference between the waves is 180 degrees (anti-phase), meaning the peak of one wave meets the trough of the other. Additionally, the path difference must be an odd multiple of half the wavelength.

What is the mathematical condition for destructive interference?

The mathematical condition for destructive interference is that the path difference must be equal to (n + 0.5) times the wavelength, where 'n' is an integer.