Derivatives of inverse functions | Advanced derivatives | AP Calculus AB | Khan Academy
Summary
TLDRThe video explains the relationship between a function and its inverse, particularly focusing on their derivatives. Using the chain rule, the instructor derives a formula connecting the derivative of a function to the derivative of its inverse. By applying this concept to specific functions like \( e^x \) and its inverse, the natural log, the video demonstrates how this relationship holds true. This technique offers a useful method for calculating the derivative of an inverse function. The video encourages viewers to review inverse functions and apply calculus concepts for deeper understanding.
Takeaways
- 🧮 Inverse functions have the property that g(f(x)) = x, where g(x) is the inverse of f(x).
- 🔄 If f maps x to a value f(x), then the inverse function g takes f(x) back to x.
- 📝 The chain rule can be applied to find the derivative of inverse functions.
- 📉 Taking the derivative of both sides of g(f(x)) = x results in a useful relationship between the derivatives of a function and its inverse.
- ⚙️ Using the chain rule, we find that f'(x) = 1 / g'(f(x)).
- 🔍 This equation provides a link between the derivative of a function and the derivative of its inverse.
- 📚 For example, when f(x) = e^x, its inverse is g(x) = ln(x).
- 💡 The derivative of e^x is e^x, and the derivative of ln(x) is 1/x, supporting the derived relationship.
- 🔄 The formula holds true for other functions as well, verifying the relationship between inverse functions and their derivatives.
- 🧠 This concept helps in understanding and computing the derivative of an inverse function more efficiently.
Q & A
What is the relationship between two functions that are inverses of each other?
-If f(x) and g(x) are inverse functions, then applying g to f(x) (or f inverse of f(x)) results in x, meaning g(f(x)) = x.
How do inverse functions map values?
-An inverse function g maps the output of f(x) back to the original input x. If f(x) takes x to f(x), then g(f(x)) brings it back to x.
What rule is applied to find the derivative of inverse functions?
-The chain rule is applied to find the derivative of inverse functions, leading to a relationship between the derivatives of a function and its inverse.
How do you express the relationship between the derivatives of inverse functions?
-The derivative of f(x), f'(x), is equal to 1 divided by the derivative of g at f(x), or f'(x) = 1 / g'(f(x)).
Why is the relationship between the derivatives of inverse functions useful?
-This relationship allows you to calculate the derivative of an inverse function if you know the derivative of the original function.
What happens when you differentiate the equation g(f(x)) = x using the chain rule?
-Using the chain rule, the derivative of g(f(x)) = x results in g'(f(x)) * f'(x) = 1, which helps derive the formula f'(x) = 1 / g'(f(x)).
How can you verify the derivative relationship for exponential and logarithmic functions?
-For f(x) = e^x and g(x) = ln(x), f'(x) = e^x and g'(x) = 1/x. Substituting into the formula f'(x) = 1 / g'(f(x)) confirms the result.
What is the derivative of e^x, and why is it significant?
-The derivative of e^x is e^x itself, which is a unique and important result in calculus because the function equals its own derivative.
What is the derivative of the natural logarithm function?
-The derivative of the natural logarithm function ln(x) is 1/x.
Can you use the derivative relationship to find the derivative of inverse functions without directly differentiating them?
-Yes, using the relationship f'(x) = 1 / g'(f(x)), you can deduce the derivative of an inverse function by knowing the derivative of the original function.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
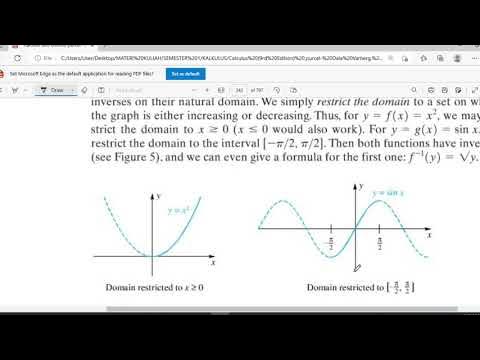
Fungsi Transenden 2 (Invers Fungsi dan Turunannya)

📚 Derivada - Definição e Cálculo - Cálculo 1 (#16)

FUNGSI INVERS KELAS 11, KONSEP DAN CONTOH SOAL mudah dipahami

Matematika Teknik I: 101 Fungsi Logaritma Natural - Definisi ln x dan turunannya
What does area have to do with slope? | Chapter 9, Essence of calculus
Graphing Inverse Functions
5.0 / 5 (0 votes)
