Pensamiento matemático 3. Progresión 2a. Origenes del calculo.

Summary

En este vídeo, se exploran los orígenes del cálculo diferencial y integral, enfocándose en cuatro problemas fundamentales: la recta tangente, la velocidad y aceleración de vehículos, el cálculo de áreas bajo curvas y los problemas de máximos y mínimos en optimización. Se mencionan conceptos clave como el plano cartesiano, las rectas y las curvas cónicas, como parábolas, circunferencias y elipses, y se promete un análisis detallado de sus funciones en futuras sesiones.

Takeaways

• 📐 El primer problema de cálculo mencionado es la recta tangente, que es una línea que toca una curva en un solo punto.
• 🚗 El segundo problema se refiere a la velocidad y aceleración de un vehículo, que son temas clave en el cálculo diferencial.
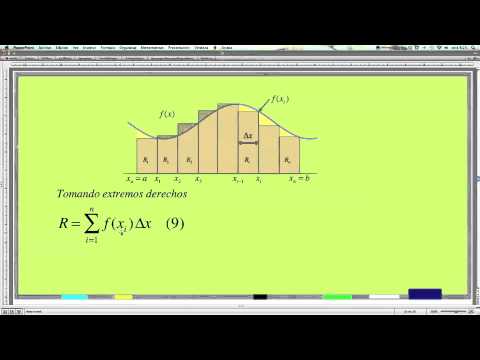
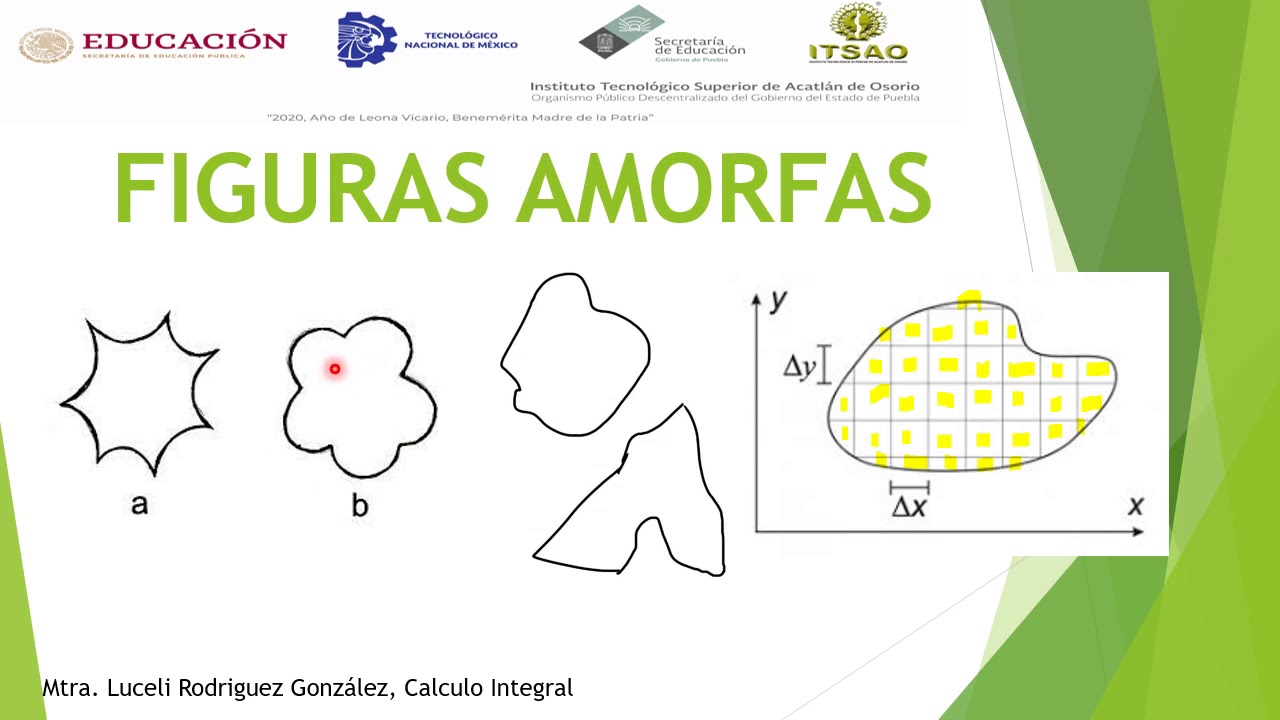
• 📉 El tercer punto trata sobre el cálculo de áreas bajo curvas, un tema central en el cálculo integral.
• 📏 El cuarto problema discute la longitud de curvas y el volumen, que también son problemas originarios del cálculo.
• 🔍 Se menciona que los problemas de cálculo también incluyen la búsqueda de máximos y mínimos, es decir, la optimización.
• 📋 Se destaca la importancia del plano cartesiano y su utilización en el cálculo, incluyendo el dominio y el contradominio de una función.
• 📘 Se habla sobre la necesidad de repasar conceptos de geometría analítica, como las ecuaciones de líneas rectas.
• 📊 Se menciona que cada curva en un plano cartesiano se puede representar mediante una función y una tabla de valores.
• 🌐 Se anuncia que en un próximo video se explorarán las características y funciones de las curvas conicas como la parábola, la circunferencia y la elipse.
• 🔢 Se enfatiza la importancia de entender las diferentes curvas y sus funciones asociadas en el contexto del cálculo.

Q & A

¿Cuáles son los cuatro problemas que dieron origen al cálculo?

Los cuatro problemas que dieron origen al cálculo son: la recta tangente, la velocidad y aceleración de un vehículo, el cálculo del área bajo una curva y los problemas de máximos y mínimos o de optimización.

¿Qué problema se refiere a la recta tangente y cómo se relaciona con el cálculo?

La recta tangente es una recta que toca en un solo punto a una curva. Determinar la recta tangente en un punto dado de la curva es un problema de cálculo que se aborda para entender la tasa de cambio instantáneo de una función en ese punto.

¿Cómo está relacionada la velocidad de un vehículo con el cálculo?

La velocidad de un vehículo, que se determina por la distancia y el tiempo, está relacionada con el cálculo porque implica entender cómo la velocidad cambia con el tiempo, lo que conduce a conceptos de derivadas y aceleración.

¿Qué problema se refiere al cálculo del área bajo una curva y por qué es importante?

El problema de calcular el área bajo una curva es importante en el cálculo integral. Sirve para entender la cantidad total de una variable fluyendo bajo la curva de otra, lo que es esencial en muchas aplicaciones prácticas, como en física y economía.

¿Cuál es la relación entre los problemas de máximos y mínimos y la optimización?

Los problemas de máximos y mínimos son una parte fundamental de la optimización. Consisten en encontrar el valor que maximiza o minimiza una función dada, lo cual es crucial en áreas como la ingeniería, la economía y la investigación operativa.

¿Qué es el plano cartesiano y cómo se relaciona con el cálculo?

El plano cartesiano es un sistema de coordenadas bidimensional formado por dos ejes perpendiculares, el eje de las x y el eje de las y. Es fundamental en el cálculo analítico, ya que permite representar gráficamente funciones y resolver problemas geométricos y algebraicos.

¿Cómo se expresa la ecuación de una línea recta en el contexto del cálculo?

En el cálculo, la ecuación de una línea recta se expresa en la forma y = mx + b, donde m es la pendiente de la línea y b es el término independiente.

¿Qué son las curvas bajo la cónica y cuáles son algunas de las más comunes?

Las curvas bajo la cónica son aquellas que se pueden obtener como la intersección de una superficie cónica con un plano. Algunas de las más comunes son la parábola, la circunferencia y la elipse.

¿Cómo se relaciona la parábola con una función matemática?

Una parábola se relaciona con una función matemática a través de la función f(x) = ax^2 + bx + c, donde a no es cero. Esta función representa la ecuación de una parábola en el plano cartesiano.

¿Qué es la función de una circunferencia en el plano cartesiano?

La función de una circunferencia en el plano cartesiano generalmente se escribe en la forma (x - h)^2 + (y - k)^2 = r^2, donde (h, k) es el centro de la circunferencia y r es su radio.

¿Cuál es la importancia de las tablas de valores en el cálculo?

Las tablas de valores son importantes en el cálculo porque proporcionan una manera de entender la relación entre la entrada (dominio) y la salida (contradominio) de una función, lo que es esencial para visualizar y analizar el comportamiento de la función.