DERIVADAS | MATEMÁTICA APLICADA.

Erich Argel

7 Jun 202308:12

Summary

TLDREl script explora el origen y aplicaciones fundamentales de la derivada en matemáticas, destacando su importancia en problemas antiguos como la velocidad, área bajo curvas, rectas tangentes y máximos y mínimos. Se ilustra con un ejemplo práctico de optimización en economía, donde se busca el tamaño del pedido óptimo para minimizar costos. La derivada se utiliza para encontrar puntos críticos y determinar el mínimo costo total de 480 equipos clínicos. Destaca cómo la derivada es esencial en ciencia, tecnología, economía y la vida cotidiana, ayudando a la toma de decisiones eficientes.

Takeaways

📚 La derivada es un concepto fundamental del cálculo diferencial que tiene sus orígenes en la antigua Grecia y surge para resolver cuatro problemas clave: la velocidad, el área bajo una curva, la recta tangente y los máximos y mínimos.
📈 La derivada es una herramienta matemática utilizada para calcular la respuesta de una función cuando se alteran sus valores iniciales.
📉 Representada gráficamente, la derivada de una función se observa cuando se superpone una línea recta a una curva, indicando la pendiente de la función en ese punto.
🔍 La determinación de la derivada no es solo un punto de vista teórico, sino que tiene una serie de aplicaciones vitales en diferentes campos, como la ingeniería física, los negocios y la economía.
📝 Un ejemplo práctico de aplicación de las derivadas es el cálculo del costo total en un pedido, utilizando la fórmula cdx = 4x + 720 + 921.600/x, donde x es el número de equipos clínicos.
🔑 La optimización de una función, como encontrar sus valores máximos y mínimos, es una de las aplicaciones más importantes de la derivada y es fundamental para resolver problemas en termodinámica, física y economía.
📉 Para encontrar el tamaño del pedido que minimiza el costo total, es necesario realizar un proceso de optimización utilizando la derivada de la función de costo.
🔍 El proceso de optimización implica reescribir la función y calcular su derivada para encontrar los puntos críticos, donde la derivada es cero.
📊 Una vez que se encuentran los puntos críticos, se evalúan para determinar cuál de ellos minimiza el costo total, como en el caso del ejemplo donde se buscaba el número óptimo de equipos clínicos.
📌 El ejemplo del costo total muestra que la derivada es una herramienta esencial para ayudar a las empresas a tomar decisiones de optimización y a economizar de manera eficiente.
🌐 La derivada tiene una amplia gama de aplicaciones en la ciencia, la tecnología, la economía y en la vida diaria, siendo una parte integral de la matemática moderna.

Q & A

¿Cuál es el origen de la derivada en el ámbito de la matemática?
-La derivada, considerada como el eje principal del cálculo diferencial, tiene su origen en la antigua Grecia y surge como resultado de cuatro problemas fundamentales: la velocidad, el área bajo la curva, la recta tangente y los máximos y mínimos.
¿Qué es una derivada y cómo se representa gráficamente?
-Una derivada es un elemento utilizado en la matemática para calcular respuestas de una función a la que se le están alterando sus valores iniciales. Está representada gráficamente cuando una línea recta se superpone sobre cualquier curva, indicando la pendiente de la función respecto al eje sobre el cual se está estudiando.
¿Por qué son importantes las derivadas en el ámbito de la ingeniería física y otros campos?
-Las derivadas son importantes porque tienen una serie de aplicaciones vitales en la ingeniería física, negocios y economía, permitiendo calcular áreas, optimizar costos y resolver problemas relacionados con la maximización de ganancias, entre otros.
¿Qué es un punto crítico en el contexto de las funciones matemáticas?
-Un punto crítico es aquel donde la derivada de la función es cero, lo que significa que no existe una variación en el valor de la función en ese punto específico.
¿Cómo se definen los costos fijos y variables en relación con la optimización de costos?
-Los costos fijos son aquellos que no dependen de la cantidad producida, mientras que los costos variables se incrementan o disminuyen en función del número de unidades fabricadas. La optimización de costos busca encontrar los valores que minimizan el costo total.
¿Qué significa optimizar una función y cómo se relaciona con las derivadas?
-Optimizar una función consiste en encontrar sus valores máximos y mínimos, es decir, determinar los valores en el dominio de la función para los cuales se alcanza el máximo o mínimo. Las derivadas son fundamentales en este proceso, ya que permiten identificar los puntos críticos donde podrían ocurrir estos valores extremos.
¿Cómo se plantea el problema de optimización en el script proporcionado?
-El problema de optimización planteado en el script es determinar el tamaño del pedido que minimiza el costo total, dado por la función cdx = 4x + 720 + 921.600/x, siendo x el número de equipos clínicos.
¿Cómo se reestructura la función para encontrar el punto crítico en el problema de optimización del costo total?
-Para encontrar el punto crítico, se reestructura la función de costo total como cdx = 4x + 720 + (921.600/x - 1), y luego se toma la derivada de esta expresión para igualarla a cero y resolver para x.
¿Cuál es el resultado de la derivada de la función de costo total presentada en el script?
-La derivada de la función de costo total, c'(x), es igual a 4 - (921.600/x^2), donde 4 es la derivada de 4x, 0 es la derivada de la constante 720, y -(921.600/x^2) es la derivada de (921.600/x - 1).
¿Cómo se determina el tamaño del pedido que minimiza el costo total según el script?
-Para determinar el tamaño del pedido que minimiza el costo total, se iguala a cero la derivada de la función de costo total y se resuelve la ecuación resultante, encontrando que x = 480, lo que indica que el pedido que minimiza el costo total es de 480 equipos clínicos.
¿En qué áreas se aplican las derivadas más allá del ámbito académico?
-Las derivadas se aplican en áreas como la ciencia, la tecnología, la economía y en la vida diaria de las personas, ayudando a determinar tamaños de pedidos, tiempos de entrega, ganancias máximas y muchos otros aspectos.

Outlines

00:00

📚 Origen y Aplicaciones de la Derivada

El primer párrafo introduce la derivada como un concepto fundamental del cálculo diferencial, con raíces en la antigua Grecia y asociada a cuatro problemas clave: la velocidad, el área bajo una curva, la recta tangente y los máximos y mínimos. Se describe cómo la derivada, representada gráficamente por una línea tangente a una curva, es utilizada para estudiar el cambio de una función cuando se alteran sus valores iniciales. Además, se menciona que la derivada no solo tiene un valor teórico sino que tiene aplicaciones prácticas en áreas como la ingeniería física, los negocios y la economía, como se ejemplifica con un problema de optimización del costo total de un pedido de equipos clínicos.

05:00

🔍 Proceso de Optimización y Cálculo de la Derivada

El segundo párrafo se enfoca en el proceso de optimización a través de la derivada, utilizando el ejemplo del costo total de un pedido de equipos clínicos. Se describe cómo se reescribe la función de costo total para facilitar el cálculo de su derivada. Luego, se procede a encontrar los puntos críticos, que son los valores donde la derivada es cero, indicando posibles máximos o mínimos. El texto guía a través de los pasos para resolver la ecuación y encontrar el tamaño del pedido que minimiza el costo, que resulta ser de 480 equipos. El párrafo concluye destacando la importancia de la derivada en la matemática y su aplicación en diversas disciplinas y áreas de la vida cotidiana, como la economía y la gestión empresarial.

Mindmap

Keywords

💡Derivada

La derivada es un concepto fundamental del cálculo diferencial, que se utiliza para calcular la tasa de cambio de una función en un punto específico. En el video, la derivada es presentada como una herramienta para resolver problemas antiguos y modernos, como la velocidad, el área bajo una curva, la recta tangente y la localización de máximos y mínimos. Se relaciona con el tema principal al ser una herramienta clave para la optimización y la determinación de puntos críticos en la función de costos del ejemplo dado.

💡Optimización

La optimización se refiere al proceso de encontrar los valores máximos o mínimos de una función, lo cual es una de las aplicaciones destacadas de las derivadas. En el contexto del video, la optimización es usada para determinar el tamaño del pedido que minimiza el costo total, lo que es un ejemplo práctico de cómo las derivadas pueden ser aplicadas en problemas de negocio y economía.

💡Puntos críticos

Los puntos críticos son los valores en los que la derivada de una función es cero o no existe, y son esenciales para la identificación de máximos y mínimos. En el video, se menciona la importancia de encontrar puntos críticos al resolver el problema de optimización del costo total, donde se busca el número óptimo de equipos clínicos que se deben pedir.

💡Costo total

El costo total es la suma de los costos fijos y variables asociados a la producción de un bien o servicio. En el video, se presenta una ecuación de costo total que incluye términos fijos y variables, y se utiliza para encontrar el tamaño del pedido que minimiza este costo mediante el uso de derivadas.

💡Función

Una función en matemáticas es una relación que asigna un único valor de salida para cada valor de entrada. En el tema del video, la función representa el costo total en relación con la cantidad de equipos clínicos, y se manipula para encontrar su derivada y los puntos críticos que indican la optimización del costo.

💡Área bajo la curva

El cálculo del área bajo una curva es una de las aplicaciones históricas de las derivadas, donde se utiliza para determinar volúmenes y áreas en geometría analítica. Aunque no se utiliza directamente en el ejemplo del video, es mencionado como uno de los problemas fundamentales que dio origen a la derivada.

💡Recta tangente

La recta tangente es una línea que toca una curva en un solo punto sin cruzarla, y su pendiente es igual a la derivada de la función en ese punto. En el video, la recta tangente se menciona como uno de los problemas que condujeron al desarrollo de las derivadas.

💡Máximos y mínimos

Los valores máximos y mínimos de una función son puntos donde la función alcanza su valor más alto o bajo en un determinado intervalo. En el video, la búsqueda de estos valores es crucial para la optimización del costo total, ya que se desean encontrar los puntos en los que el costo es mínimo.

💡Ingeniería física

La ingeniería física es una rama de la ingeniería que aplica el conocimiento de las ciencias físicas a la resolución de problemas técnicos. En el video, se menciona que las derivadas tienen aplicaciones vitales en la ingeniería física, aunque no se da un ejemplo específico, implica que las derivadas son esenciales para el análisis y diseño en este campo.

💡Negocios y economía

El video destaca que las derivadas tienen aplicaciones en los negocios y la economía, donde se utilizan para problemas de optimización y toma de decisiones basadas en el análisis de costos y beneficios. El ejemplo del costo total y el tamaño del pedido que se debe minimizar es un claro reflejo de cómo las derivadas pueden ser aplicadas en estos ámbitos.

Highlights

La derivada es considerada el eje principal del cálculo diferencial y tiene su origen en la antigua Grecia.

La derivada surge como resultado de cuatro problemas fundamentales: la velocidad, el área bajo la curva, la recta tangente y los máximos y mínimos.

La derivada es un elemento utilizado en la matemática para calcular respuestas de una función a cambios en sus valores iniciales.

La derivada de una función se representa gráficamente mediante una línea recta que se superpone sobre una curva.

El valor de la pendiente de la derivada respecto al eje es conocido como el derivado.

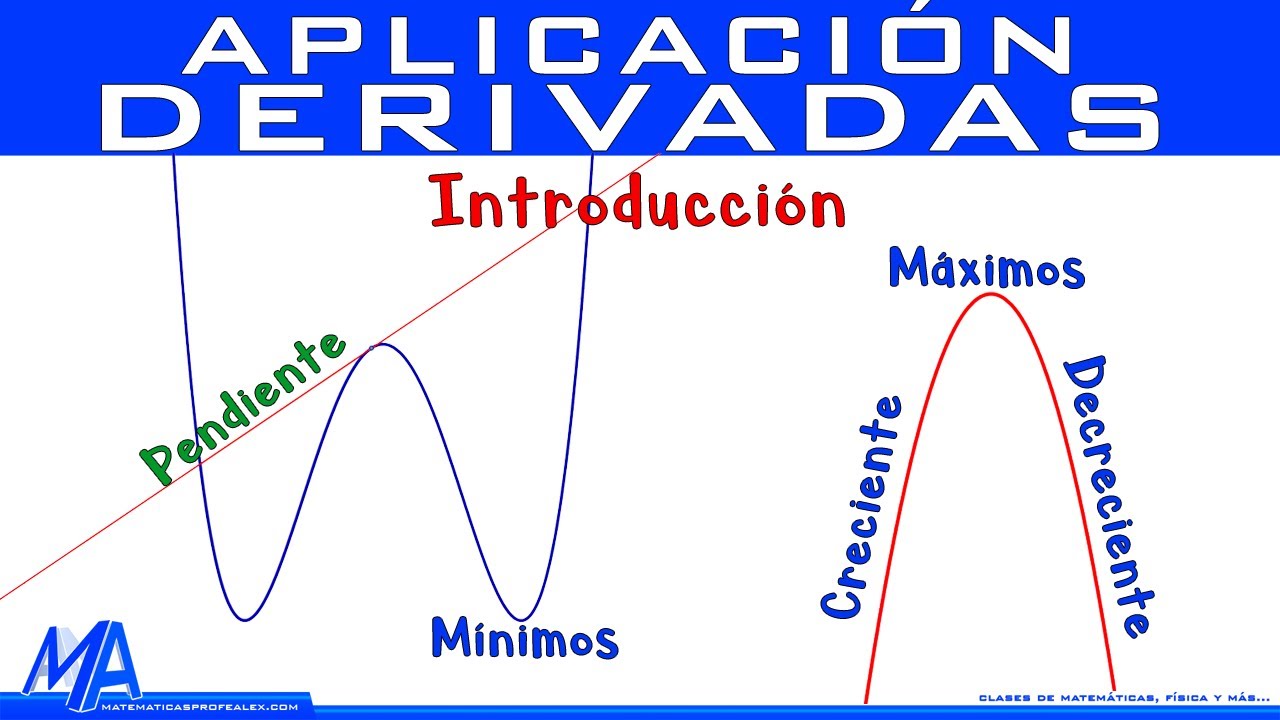
La aplicación de la derivada va más allá del ámbito teórico y tiene aplicaciones vitales en diversos campos.

Las derivadas son fundamentales en la ingeniería física, negocios y economía.

Se plantea un ejercicio para determinar el tamaño del pedido que minimiza el costo total, utilizando una función dada.

El costo total es la suma de los costos fijos y los costos variables, que dependen de la cantidad producida.

Para optimizar una función, se buscan sus valores máximos y mínimos en su dominio.

Los puntos críticos son donde la derivada de la función es cero.

El proceso de optimización es una de las aplicaciones más importantes de la derivada.

Se describe un método para reescribir y reestructurar la función dada para encontrar su derivada.

Se calcula la derivada de la función dada, simplificando y encontrando la expresión para c'(x).

Para encontrar los puntos críticos, se iguala la primera derivada a cero y se resuelve la ecuación.

Se resuelve la ecuación 4 - 921.600x^(-2) = 0 para encontrar el tamaño del pedido que minimiza el costo total.

Se determina que el tamaño del pedido que minimiza el costo total es de 480 equipos clínicos.

La derivada tiene una gran cantidad de aplicaciones en la ciencia, la tecnología, la economía y en la vida cotidiana.