ESTADISTICA DESCRIPTIVA.- PARAMETROS DE CENTRALIZACION Y DISPERSION.
Summary
TLDREste vídeo tutorial explica conceptos estadísticos como la moda, mediana y media, utilizando los personajes de 'Los Simpson' como ejemplo. Se calcula la mediana, moda y media de una muestra de 9 habitantes, y se procede a analizar la dispersión de datos mediante el rango, la desviación media, la varianza y la desviación típica. Además, se introduce el coeficiente de variación para comparar la dispersión en diferentes muestras.
Takeaways
- 😀 El vídeo trata sobre estadísticas y cómo se pueden calcular los parámetros de descentralización y dispersión utilizando ejemplos sencillos.
- 👨🏫 Se explica que para estudios complejos, en lugar de preguntar a toda la población, se elige una muestra representativa para realizar los cálculos estadísticos.
- 🔢 Se calcula la mediana como el valor central en una lista ordenada de datos, siendo más fácil de entender cuando hay un número impar de datos.
- 📊 Se menciona la moda como el valor que se repite con mayor frecuencia en los datos, y cómo puede cambiar dependiendo de la muestra elegida.
- 📈 Se describe cómo calcular la media aritmética, que es el promedio de los datos, sumando todos los valores y dividiendo por la cantidad de datos.
- 📉 Se explica la descentralización a través del rango, que es la diferencia entre el valor máximo y mínimo en los datos.
- 📊 Se detalla la desviación media, que es el promedio de las distancias de cada dato respecto a la media, y cómo se calcula.
- 📈 Se habla sobre la varianza, que es el promedio de las distancias al cuadrado de cada dato respecto a la media, y su importancia en la medición de la dispersión.
- 🔍 Se introduce la desviación típica como la raíz cuadrada de la varianza, proporcionando una medida de la dispersión en términos de la unidad de los datos.
- 📊 Se explica el coeficiente de variación, que es una medida de la dispersión en proporción al valor representativo de la muestra, y cómo se utiliza para comparar muestras.
Q & A
¿Qué parámetros de descentralización se discuten en el vídeo?
-El vídeo trata sobre la moda, la mediana y la media como parámetros de descentralización.
¿Cómo se define la moda según el vídeo?
-La moda es el valor que se repite con más frecuencia en un conjunto de datos.
¿Cuál es la fórmula para calcular la mediana cuando se tienen datos ordenados?
-Si el número de datos es impar, la mediana es el valor central. Si es par, es el promedio de los dos valores centrales.
¿Cómo se calcula la media de una muestra?
-La media se calcula sumando todos los valores de la muestra y dividiendo el resultado por la cantidad total de valores.
¿Qué significa el rango en el contexto del vídeo?
-El rango es la diferencia entre el valor más grande y el más pequeño en un conjunto de datos, indicando la dispersión de la muestra.
¿Qué es la desviación media y cómo se calcula?
-La desviación media es el promedio de las distancias absolutas que cada dato se aleja de la media. Se calcula restando la media a cada dato y luego tomando el valor absoluto, sumando todos estos valores y dividiendo por la cantidad de datos.
¿Cuál es la fórmula para calcular la varianza?
-La varianza se calcula sumando los valores de las desviaciones al cuadrado de cada dato, dividiendo por la cantidad de datos y luego tomando la raíz cuadrada del resultado.
¿Qué es la desviación típica y cómo se relaciona con la varianza?
-La desviación típica es la raíz cuadrada de la varianza, indicando la magnitud promedio de la dispersión de los datos alrededor de la media.
¿Cómo se calcula el coeficiente de variación?
-El coeficiente de variación se calcula dividiendo la desviación típica por la media y multiplicando por 100 para obtener un porcentaje que indica la dispersión relativa en relación con la media.
¿Qué implica el coeficiente de variación en el análisis estadístico?
-El coeficiente de variación permite comparar la dispersión de diferentes conjuntos de datos, proporcionando una medida de la variabilidad relativa en términos del valor representativo de la muestra.
¿Cuál es la importancia de entender los parámetros de descentralización y dispersión en la estadística?
-Los parámetros de descentralización y dispersión son cruciales para entender la variabilidad de los datos, comparar diferentes muestras y hacer inferencias sobre la población de la que provienen los datos.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Media, Mediana y Moda para datos agrupados puntualmente

MEDIDAS DE TENDENCIA CENTRAL Super facil – Para principiantes

Medidas de tendencia central

MEDIA, MODA y MEDIANA Muy Fácil - Medidas de Tendencia Central
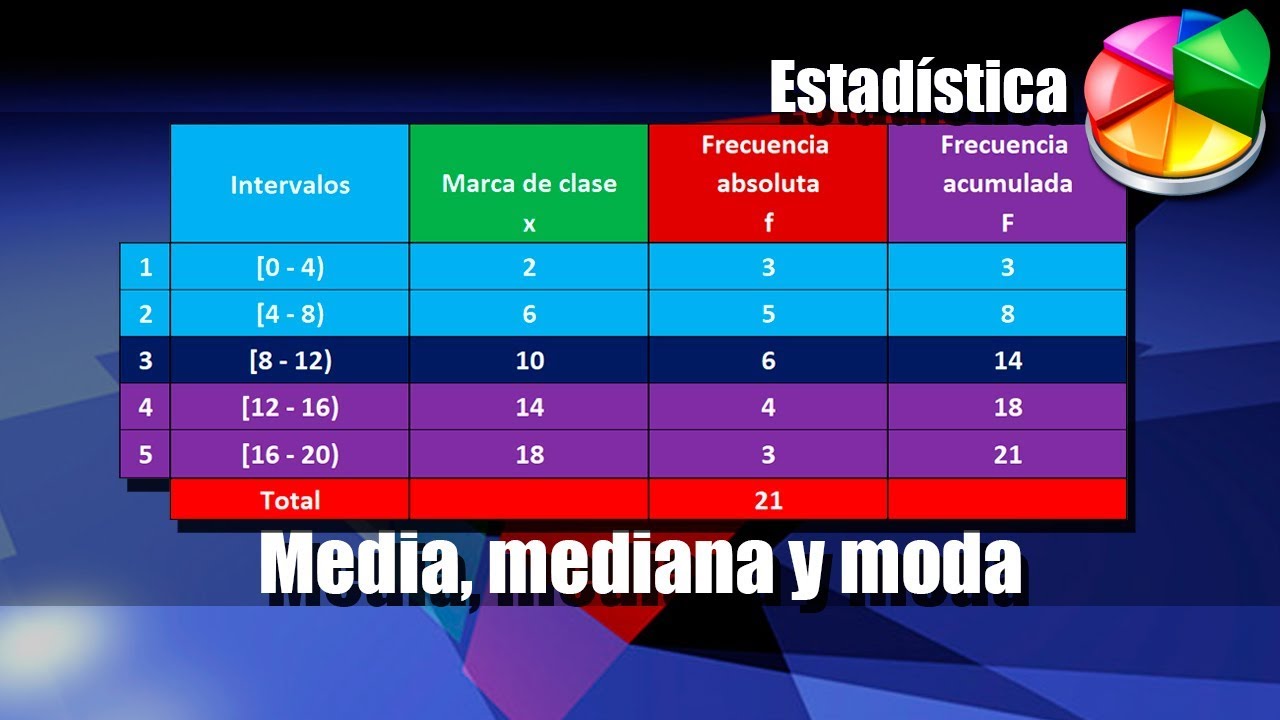
Media, Mediana y Moda para Datos Agrupados en Intervalos
Parámetros de posición: mediana, cuartiles, deciles y percentiles, estadística descriptiva

Medidas de tendencia central ¿Qué significan y cómo se interpretan?
5.0 / 5 (0 votes)