Biot Savart law (vector form) | Moving charges & magnetism | Khan Academy
Summary
TLDRThis video explores how to calculate the magnetic field produced by a current-carrying wire, focusing on the Biot-Savart Law. The law involves analyzing tiny segments of the wire and using vector equations to determine the magnetic field's strength at a given point. The video explains the relationship between current, distance, angle, and the magnetic field. It also introduces constants like permeability and demonstrates techniques like the right-hand rule and cross products to find the magnetic field's direction. Ultimately, it highlights how magnetic fields are calculated through integration for entire wires.
Takeaways
- 🔋 Current-carrying wires generate a magnetic field around them, calculable via the Biot-Savart law.
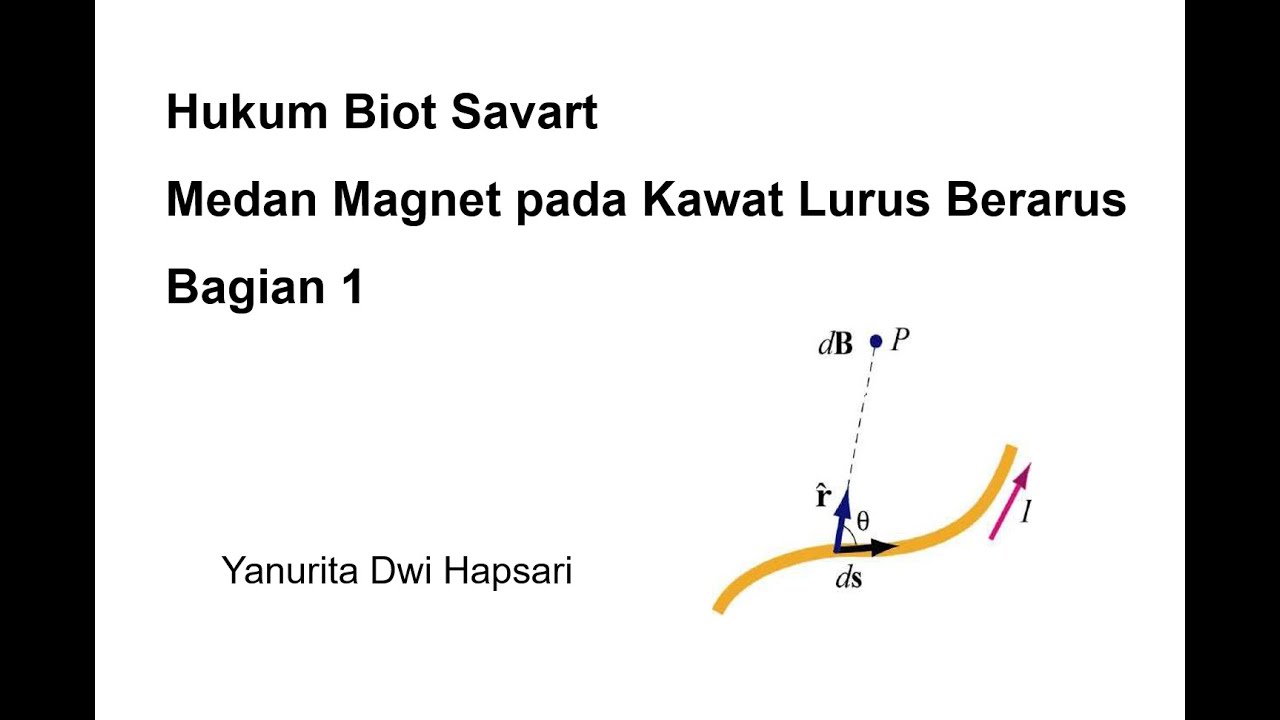
- 🧲 To apply the Biot-Savart law, you must focus on a small segment of the wire, not the entire length.
- 📏 The law involves calculating the magnetic field due to a tiny wire segment of length 'dl' at a distance 'r' from the segment.
- ✖️ The magnetic field, represented by 'dB', is a vector and calculated using a cross-product involving 'dl' and 'r'.
- 📐 The magnitude of the magnetic field depends on current (I), the length of the current element (dl), and the sine of the angle between dl and r.
- 🌀 Magnetic field strength decreases as the distance from the current element increases, following an inverse-square law (1/r²).
- 📏 The magnetic field is strongest at 90 degrees relative to the current element and weakest (or zero) along the axis (0 or 180 degrees).
- 🧲 The constant μ₀ (permeability of free space) is a fundamental value, approximately 4π × 10⁻⁷ Tesla meters per Ampere.
- 👋 The direction of the magnetic field can be determined using the right-hand clasp rule or by using the vector cross-product.
- 🔄 To calculate the total magnetic field of the entire wire, sum the contributions of all small segments (integral).
Q & A
What is the Biot-Savart law, and why is it important in calculating magnetic fields?
-The Biot-Savart law is a fundamental equation in magnetism that describes the magnetic field produced by a current-carrying element of wire. It is important because it allows the calculation of the magnetic field's strength and direction at any point in space around the wire.
Why can't we calculate the magnetic field for the entire wire at once using the Biot-Savart law?
-The Biot-Savart law requires dividing the wire into infinitesimally small elements (dl) to calculate the magnetic field, as it only applies to small current elements. Summing the magnetic field contributions of each tiny element gives the total magnetic field around the entire wire.
What does the vector form of the Biot-Savart law tell us about the magnetic field?
-The vector form of the Biot-Savart law shows that the magnetic field (dB) is a vector that depends on the current (I), the length of the wire element (dl), the unit vector in the direction of the point of interest (r̂), and the distance from the current element (r). It also includes a cross product, which means the magnetic field depends on the angle between the current element and the position vector.
How does the magnitude of the magnetic field vary with distance from the wire?
-The magnitude of the magnetic field decreases with the square of the distance from the wire, following the inverse-square law (1/r²). This means that the farther you are from the wire, the weaker the magnetic field becomes.
What role does the angle (θ) play in the Biot-Savart law?
-The angle θ is the angle between the direction of the current element (dl) and the position vector (r̂). The magnetic field is proportional to the sine of this angle (sinθ), meaning the magnetic field is strongest when θ = 90° and zero when θ = 0° or 180°.
What is the significance of the constant μ₀ in the Biot-Savart law?
-The constant μ₀, called the permeability of free space, determines the strength of the magnetic interaction in a vacuum. Its value is 4π × 10⁻⁷ T·m/A, and it plays a similar role to the permittivity constant in Coulomb's law for electric fields.
How do you determine the direction of the magnetic field produced by a current element?
-The direction of the magnetic field is determined using the right-hand rule. Point your thumb in the direction of the current, and your fingers will curl in the direction of the magnetic field around the wire. Alternatively, the direction can be found using the cross product of dl and r̂.
Why does the magnetic field differ from that of an electric field in terms of directionality?
-Unlike electric fields, which radiate uniformly from a point charge, the magnetic field produced by a current-carrying wire is directional due to the cross product between the current element and the position vector. This creates a magnetic field that is strongest perpendicular to the current and zero along the current's axis.
What happens to the magnetic field at different points around the current element?
-At points perpendicular to the current element, the magnetic field is at its maximum because the angle between the current and the position vector is 90°, making sinθ = 1. At points along the current’s axis, the magnetic field is zero since the angle is 0° or 180°, making sinθ = 0.
How can you calculate the total magnetic field around a wire using the Biot-Savart law?
-To calculate the total magnetic field around a wire, you must integrate the magnetic field contributions (dB) from each infinitesimal current element (dl) over the entire length of the wire. This integration accounts for all the small magnetic fields generated by each segment of the wire.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Derivation of the Biot-Savart law and calculating the magnetic field of a long straight wire.
Hukum Biot Savart Bagian 1- Medan Magnet oleh Kawat Lurus Berarus - Fisika 2 Bab 4

Soal & pembahasan || KEMAGNETAN kelas IX Semester genap

Medan Magnetik • Part 5: Gaya Lorentz Pada Kawat Berarus Listrik

Fisika kelas 12 | Medan magnet #part1

FISIKA Kelas 12 - Gaya Magnetik | GIA Academy
5.0 / 5 (0 votes)
