SUMAS DE RIEMANN

Summary

El guion del video explica conceptos fundamentales del cálculo integral, centrándose en las sumas de Riemann. Se describe cómo se calcula el área bajo una curva utilizando rectángulos, diferenciando entre sumas inferiores y superiores. Se enfatiza la importancia de la base constante de los rectángulos y cómo la altura varía según la función. El video utiliza Geogebra para ilustrar cómo mejorar la aproximación al área al aumentar el número de rectángulos, concluyendo que, con un número suficientemente grande, ambas metodologías de sumas son igualmente efectivas para determinar el área bajo la curva.

Takeaways

• 📚 El cálculo integral se utiliza para determinar el área bajo una curva o función.
• 📐 Las sumas de Riemann son una técnica para aproximar el área bajo una curva mediante rectángulos.
• 🔢 Las sumas inferiores y superiores son dos métodos distintos para realizar estas aproximaciones.
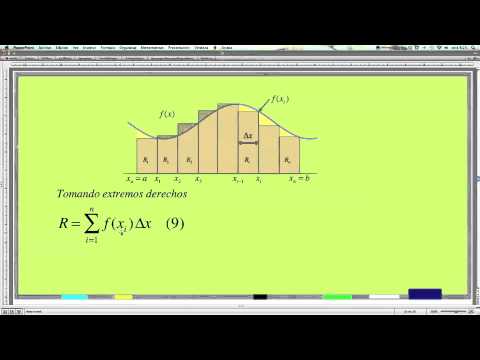
• 📏 La base de los rectángulos en las sumas de Riemann debe ser la misma para todos, mientras que la altura varía según la función.
• 📉 Las sumas inferiores colocan los rectángulos por debajo de la curva, mientras que las superiores los colocan por encima.
• 🔍 A medida que aumenta el número de rectángulos, las aproximaciones se vuelven más precisas, acercándose más a la curva.
• 📝 El límite cuando n (número de rectángulos) tiende a infinito es fundamental para obtener una aproximación exacta del área.
• 📏 Delta x (Δx) representa la base de los rectángulos y se calcula como la diferencia entre los puntos a y b dividida por n.
• 📖 La fórmula para las sumas superiores y las inferiores incluye la suma de rectángulos, donde la base y la altura varían según la función y el intervalo.
• 🔄 Con un número suficientemente grande de rectángulos, tanto las sumas inferiores como superiores pueden determinar el área debajo de la curva con igual precisión.

Q & A

¿Qué es una suma de Riemann?

Una suma de Riemann es una técnica utilizada en el cálculo integral para aproximar el área bajo la gráfica de una función en un intervalo dado. Se realiza sumando el producto de la base de los rectángulos (generalmente el intervalo dividido en subintervalos) y su altura correspondiente, que es el valor de la función en cierto punto.

¿Cuál es la diferencia entre sumas inferiores y sumas superiores en el contexto de las sumas de Riemann?

Las sumas inferiores utilizan el valor mínimo de la función en cada subintervalo para calcular la altura de los rectángulos, mientras que las sumas superiores usan el valor máximo. Esto afecta la forma en que se aproxima el área bajo la curva, ya que las sumas inferiores tienden a ser menores y las superiores mayores que el área real.

¿Para qué sirven las sumatorias en el cálculo de las sumas de Riemann?

Las sumatorias son fundamentales en el cálculo de las sumas de Riemann porque permiten sumar el área de un gran número de rectángulos, cada uno calculado con la base y la altura correspondientes. Esto es esencial para aproximar el área total bajo la curva cuando se aumenta el número de subintervalos.

¿Qué significa 'delta x' en el contexto de las sumas de Riemann?

En el cálculo de las sumas de Riemann, 'delta x' (denotado como Δx) representa la longitud de la base de los rectángulos, que es el intervalo total dividido por el número de subintervalos (n). Cuanto más grande sea n, más pequeño será Δx, lo que conduce a una mejor aproximación del área.

¿Cómo se relaciona el número de rectángulos (n) con la precisión de la aproximación en las sumas de Riemann?

A medida que aumenta el número de rectángulos (n), la base de cada rectángulo (Δx) disminuye, lo que lleva a una aproximación más precisa del área bajo la curva. Idealmente, cuando n tiende a infinito, las sumas de Riemann convergen al área exacta.

¿Qué es la fórmula general para calcular las sumas inferiores en el cálculo de Riemann?

La fórmula general para las sumas inferiores es: Área = límite cuando n tiende a infinito de la suma desde i=1 hasta n de [f(x_i^*) * Δx], donde x_i^* es el punto de mínimo en el subintervalo y Δx es la longitud de la base del rectángulo.

¿Cuál es la fórmula general para calcular las sumas superiores en el cálculo de Riemann?

La fórmula general para las sumas superiores es: Área = límite cuando n tiende a infinito de la suma desde i=1 hasta n de [f(x_i^**) * Δx], donde x_i^** es el punto de máximo en el subintervalo y Δx es la longitud de la base del rectángulo.

¿Por qué es importante que la base de los rectángulos sea la misma en todas las sumas de Riemann?

Es crucial que la base de los rectángulos sea la misma en todas las sumas de Riemann porque esto garantiza que se estén considerando rectángulos uniformes a lo largo del intervalo, lo que permite una comparación justa y una suma coherente de las áreas.

¿Cómo se determina el punto de evaluación (x_i^* o x_i^**) para las alturas de los rectángulos en las sumas de Riemann?

El punto de evaluación para las alturas de los rectángulos se determina dependiendo si se están calculando sumas inferiores o superiores. Para sumas inferiores, se toma el punto de mínimo en el subintervalo, y para sumas superiores, se toma el punto de máximo.

¿Cuál es la relación entre las sumas de Riemann y el concepto de integral definida en el cálculo?

Las sumas de Riemann son la base conceptual para el cálculo de integrales definidas. La integral definida se obtiene tomando el límite de las sumas de Riemann cuando el número de rectángulos, n, tiende a infinito, lo que proporciona el área exacta bajo la curva en el intervalo considerado.