Cálculo Diferencial: Introducción
Summary
TLDREste vídeo introductorio al curso de cálculo diferencial, presentado por Daniela, explica la importancia del cálculo diferencial en las ciencias naturales y sociales. A través de una analogía de viaje en auto, se ilustra cómo el cálculo diferencial permite calcular velocidades instantáneas, una herramienta crucial desarrollada por Newton y Leibniz. El curso abordará conceptos clave como funciones, límites y derivadas, y su aplicación en contextos reales, promoviendo la eficiencia y el entendimiento de cambios instantáneos en diversas cantidades.
Takeaways
- 📚 Este video es un curso introductorio al cálculo diferencial.
- 🚀 El cálculo diferencial es esencial para comprender descubrimientos y avances en ciencias naturales y sociales.
- 🤔 Se busca explicar la importancia del cálculo diferencial y su aplicación práctica.
- 👨🎓 Isaac Newton y Gottfried Leibniz desarrollaron el cálculo diferencial en el siglo 17.
- 🛣️ Se utiliza el ejemplo de un viaje en coche para ilustrar la necesidad de calcular velocidades instantáneas.
- 📊 La velocidad promedio no siempre representa la velocidad en un momento específico, lo cual es donde el cálculo diferencial es útil.
- 🔍 El cálculo diferencial permite inferir velocidades o aceleraciones instantáneas a partir de la posición.
- 🌟 La herramienta matemática desarrollada por Newton permitió entender conceptos como la gravedad y el movimiento.
- 📉 El cálculo diferencial también se aplica a conceptos más allá de la física, como la propagación de enfermedades o el crecimiento de costos.
- 📚 El curso se divide en tres partes: construcción de conceptos, aplicación de técnicas y análisis de ejemplos reales.
- 🔢 Se cubren temas como funciones, límites y derivadas, que son fundamentales para entender el cálculo diferencial.
Q & A
¿Qué es el cálculo diferencial y por qué es importante?
-El cálculo diferencial es una rama de las matemáticas desarrollada en el siglo 17 por Isaac Newton y Gottfried Leibniz. Es fundamental para comprender descubrimientos y avances en ciencias naturales y sociales, ya que permite calcular velocidades y aceleraciones instantáneas, así como el cambio instantáneo de una cantidad en función de otra.
¿Cuál es el objetivo del primer vídeo del curso de cálculo diferencial?
-El objetivo del primer vídeo es explicar por qué el cálculo diferencial es importante y necesario, así como presentar los temas que se abordarán en los siguientes vídeos para que el estudiante pueda entender el propósito de lo que está aprendiendo en cada momento.
¿Cómo se utiliza el cálculo diferencial en el ejemplo del viaje en automóvil?
-En el ejemplo del viaje, el cálculo diferencial se usa para calcular la velocidad instantánea en diferentes puntos del trayecto, en lugar de la velocidad promedio. Esto se hace tomando intervalos de tiempo más pequeños y calculando la razón entre la distancia recorrida y el tiempo transcurrido en esos intervalos.
¿Qué problemas presenta el cálculo diferencial para resolver en el ejemplo del viaje?
-El cálculo diferencial resuelve tres problemas principales en el ejemplo del viaje: 1) No alcanzar un valor preciso de velocidad instantánea, 2) El proceso de acercamiento es aburrido y dispendioso, y 3) Tener que repetir el proceso para calcular la velocidad en puntos diferentes.
¿Cómo se relaciona el cálculo diferencial con la física y otros campos científicos?
-El cálculo diferencial es esencial en la física para entender conceptos como la gravedad, el movimiento de los planetas y la aceleración. También se aplica en otras ciencias para medir cambios instantáneos en diversas situaciones, como la propagación de enfermedades o el aumento de costos de producción.
¿Qué es una función en el contexto del cálculo diferencial?
-Una función en el cálculo diferencial es una relación que conecta dos cantidades, donde cada valor de una cantidad (la independiente) determina un valor único de la otra cantidad (la dependiente). Por ejemplo, la posición en relación con el tiempo.
¿Qué son los límites y cómo se relacionan con la velocidad instantánea?
-Los límites son una herramienta matemática que representa el comportamiento de una función cerca de un punto específico. En el contexto de la velocidad instantánea, los límites se usan para calcular la velocidad en un punto exacto al acercar los puntos de medición lo más posible a ese punto.
¿Qué es la derivada y cómo se relaciona con el cálculo diferencial?
-La derivada es el concepto principal del cálculo diferencial y representa el cambio instantáneo de una cantidad con respecto a otra. Es la magnitud que indica la velocidad a la que una función cambia en un punto específico.
¿Cómo se estructura el curso de cálculo diferencial?
-El curso de cálculo diferencial se estructura en tres partes: el primer tercio se enfoca en construir conceptos y sus implicaciones, el segundo tercio aplica estos conceptos para encontrar derivadas de diferentes funciones, y el último tercio se centra en aplicaciones prácticas y análisis de gráficas.
¿Cuál es el propósito del cálculo diferencial en el análisis de gráficas?
-El cálculo diferencial se utiliza en el análisis de gráficas para interpretar visual y intuitivamente las derivadas, proporcionando información sobre la tasa de cambio de una función, la concavidad de la gráfica y otros aspectos relevantes.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Derivadas (Universo Mecánico 3)

¿QUÉ ES EL CÁLCULO DIFERENCIAL? Super facil - Para principiantes

🔵TRUCOS para LÍMITES: La guía completa para CALCULAR CUALQUIER LÍMITE en tu CURSO DE CÁLCULO

Aplicación de funciones matemáticas en la vida cotidiana.

PARA QUÉ SIRVE EL CÁLCULO DIFERENCIAL. LA VERDADERA RAZÓN
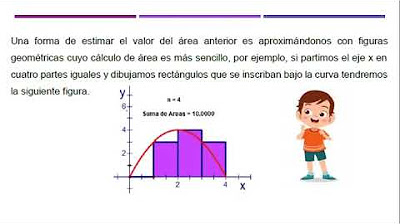
Cálculo de Áreas por Aproximación
5.0 / 5 (0 votes)