Finding Modular Inverses
Summary
TLDRThis video script explores the concept of modular inverses, focusing on how to find the multiplicative inverse of a number 'a' modulo 'M'. It explains that an inverse exists if and only if the greatest common divisor of 'a' and 'M' is one. The script provides step-by-step examples, demonstrating how to calculate the inverses of numbers like 5 mod 7, 5 mod 11, and 18 mod 19. It also introduces a shortcut for finding inverses when a number is equivalent to a negative value modulo 'M'. The script concludes with an example illustrating that no inverse exists when the greatest common divisor is greater than one, such as with 5 mod 10.
Takeaways
- 🔢 Modular inverses are multiplicative inverses that, when multiplied by a number, result in 1 modulo M.
- 🔄 A number 'a' has an inverse modulo M if and only if the greatest common divisor (GCD) of 'a' and M is 1.
- 🚫 If the GCD of 'a' and M is greater than 1, then 'a' does not have an inverse modulo M.
- 🌰 Examples are given to illustrate how to find the modular inverse, such as finding the inverse of 5 modulo 7 and modulo 11.
- 📝 The notation for expressing a modular inverse is 'a^-1 ≡ b (mod M)', indicating 'b' is the inverse of 'a' modulo M.
- ⏱️ Finding modular inverses can be time-consuming, so shortcuts are sometimes used, like recognizing that 18 is equivalent to -1 modulo 19.
- 🔁 Negative numbers can have modular inverses; for example, the inverse of -2 modulo 19 is -10, which is also 9 modulo 19.
- 💡 A shortcut for finding inverses involves using the property that a number and its negative have the same inverse modulo M.
- ❌ There is no modular inverse when the GCD of the number and the modulus is greater than 1, as shown with the example of 5 modulo 10.
- 📚 The script emphasizes the importance of understanding the relationship between GCD and the existence of modular inverses.
Q & A
What are modular inverses?
-Modular inverses are pairs of numbers that, when multiplied together, result in 1 when considering the modulus operation. Specifically, a number 'a' has an inverse mod 'M' if there exists a number 'b' such that (a * b) % M = 1.
How can you determine if a number has a modular inverse modulo M?
-A number 'a' has a modular inverse modulo 'M' if and only if the greatest common divisor (GCD) of 'a' and 'M' is equal to one. If the GCD is greater than one, there is no modular inverse.
What is the modular inverse of 5 modulo 7?
-The modular inverse of 5 modulo 7 is 3, because 5 * 3 % 7 = 1.
What is the process to find the modular inverse of a number?
-To find the modular inverse of a number 'a' modulo 'M', you start with 1 and keep adding 'M' until you find a multiple of 'a'. The quotient of that multiple divided by 'a' is the modular inverse.
What happens if the greatest common divisor between a number and the modulus is greater than one?
-If the greatest common divisor between a number 'a' and the modulus 'M' is greater than one, then 'a' does not have a modular inverse modulo 'M'.
Can you provide an example of finding the modular inverse of 5 modulo 11?
-To find the modular inverse of 5 modulo 11, you would start with 1 and keep adding 11 until you find a multiple of 5 that is congruent to 1 modulo 11. In this case, 45 is 5 times 9 and 45 % 11 = 1, so the inverse of 5 modulo 11 is 9.
Why is the inverse of 18 modulo 19 equal to 18?
-The inverse of 18 modulo 19 is 18 because 18 * 18 % 19 = 1. This is a special case where the number and its inverse are the same.
How can you find the modular inverse of a negative number modulo M?
-You can find the modular inverse of a negative number modulo 'M' by recognizing that the negative number is equivalent to a positive number modulo 'M'. For example, if you want to find the inverse of -2 modulo 19, you can see that -2 is equivalent to 17 modulo 19, and then find the inverse of 17.
What is the shortcut mentioned in the script for finding modular inverses?
-The shortcut mentioned is to recognize that if a number 'a' is equivalent to a negative number modulo 'M', you can find the inverse of the negative number and then adjust it to be positive if necessary. For example, if 'a' is equivalent to -1 modulo 'M', then 'a' is its own inverse.
Why doesn't the number 5 have a modular inverse modulo 10?
-The number 5 does not have a modular inverse modulo 10 because the greatest common divisor of 5 and 10 is 5, which is greater than one. This violates the condition that the GCD must be one for a modular inverse to exist.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

How to Convert a Negative Integer in Modular Arithmetic - Cryptography - Lesson 4

SIFAT SEDERHANA GRUP I
Inverse Functions

Komposisi Fungsi Part 3 - Fungsi invers dan Sifat-sifatnya [ Matematika Wajib Kelas X ]
Fungsi Transenden 2 (Invers Fungsi dan Turunannya)
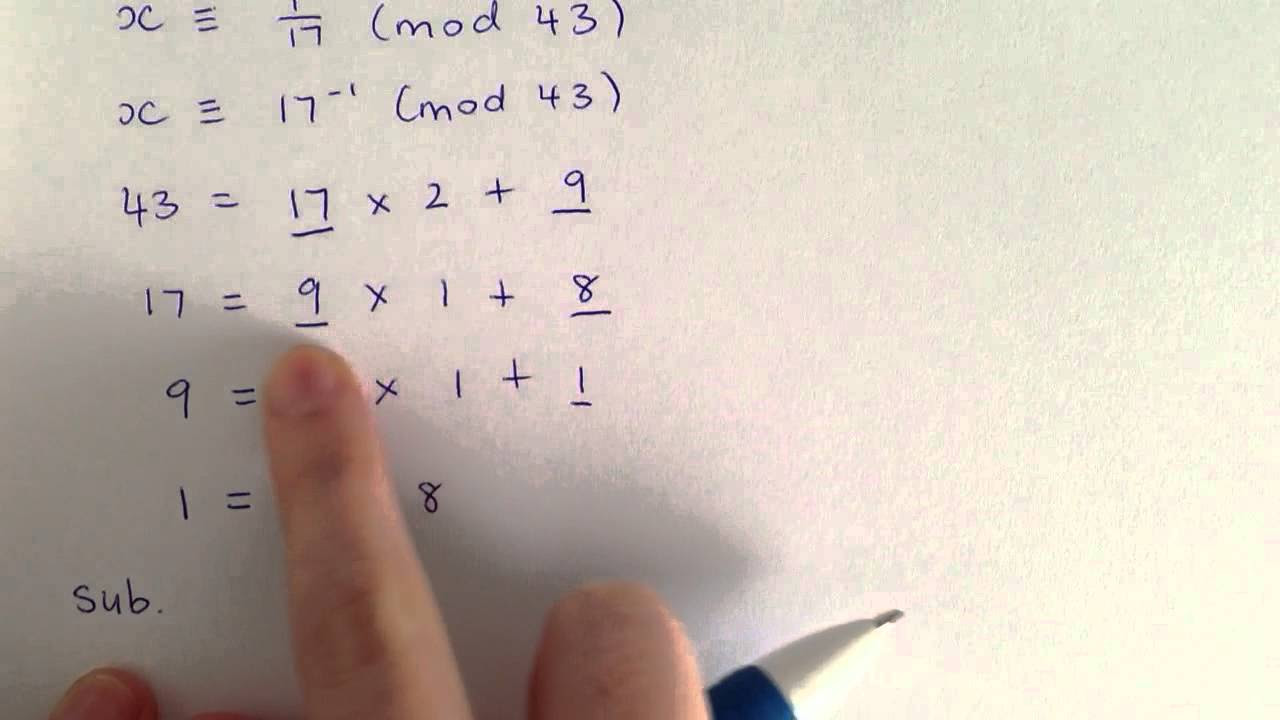
Extended Euclidean Algorithm and Inverse Modulo Tutorial
5.0 / 5 (0 votes)
