Distancia de un punto a una recta
Summary
TLDREl profesor Raúl Vega, de 'Muñoz de Cursos de Álgebra puntocom', presenta un nuevo video sobre geometría analítica, específicamente cómo calcular la distancia de un punto a una recta. Utiliza la ecuación de la recta 5x + y - 30 = 0 y el punto (5,7) como ejemplo. La fórmula para la distancia es |a * x1 + b * y1 - c| / √(a² + b²), donde a, b y c son los coeficientes de la recta y x1, y1 son las coordenadas del punto. El resultado es 4.73 unidades, y se puede racionalizar como 37√61 / 61 para cumplir con las convenciones de la geometría analítica.
Takeaways
- 📚 El script es una introducción a un nuevo canal de Geometría Analítica por el profesor Raúl Vega Muñoz.
- 🔗 Se invita a los espectadores a suscribirse al nuevo canal a través del enlace proporcionado en la descripción del video.
- 📈 El tema principal del video es el cálculo de la distancia de un punto a una recta en Geometría Analítica.
- 📐 Se presenta una ecuación de recta y coordenadas de un punto específico para ejemplificar el cálculo: la recta con ecuación 5x + y - 30 = 0 y el punto (5, 7).
- 📏 Se enfatiza que la distancia perpendicular entre el punto y la recta es la que se busca calcular.
- 📘 Se explica que la fórmula para calcular la distancia es el valor absoluto de 'a * x1 + b * y1 - c' dividido por la raíz cuadrada de 'a^2 + b^2'.
- 🔢 Se da un paso a paso para sustituir los valores en la fórmula, utilizando los coeficientes de la recta y las coordenadas del punto.
- 🧮 Se muestran los cálculos detalladamente, incluyendo potencias, multiplicaciones y el uso del valor absoluto.
- 📉 Se menciona la importancia de realizar las operaciones en la correcta jerarquía matemática para obtener el resultado.
- 📌 Se aclara que en Geometría Analítica no se utilizan decimales y se sugiere cómo racionalizar el resultado para no tener raíces en el denominador.
- 📝 El resultado final de la distancia es expresado como una fracción que no contiene raíces, ejemplificada como 37 raíz de 61 sobre 61.
Q & A
¿Quién es el creador del canal de Geometría Analítica Fácil?
-El creador del canal es el profesor Raúl Vega Muñoz.
¿En qué tema se centra el video que presenta el profesor Raúl Vega Muñoz?
-El video se centra en cómo calcular la distancia de un punto a una recta en geometría analítica.
¿Cuál es la ecuación de la recta que se utiliza en el ejemplo del video?
-La ecuación de la recta es 5x + y - 30 = 0.
¿Cuáles son las coordenadas del punto que se utiliza en el ejemplo del video?
-Las coordenadas del punto son (5, 7).
¿Qué tipo de distancia se busca calcular entre el punto y la recta en el video?
-Se busca calcular la distancia perpendicular, es decir, la que forma un ángulo de 90 grados con la recta.
¿Cuál es la fórmula para calcular la distancia de un punto a una recta en geometría analítica?
-La fórmula es: distancia = |a * x1 + b * y1 - c| / √(a² + b²), donde 'a', 'b' y 'c' son los coeficientes de la recta en su forma general y (x1, y1) son las coordenadas del punto.
¿Cómo se sustituyen los valores en la fórmula para calcular la distancia en el ejemplo del video?
-Se multiplica el valor de 'a' (5) por el valor de x1 (5), el valor de 'b' (1) por el valor de y1 (7), y se resta el valor de 'c' (30), todo ello dentro del valor absoluto y dividido por la raíz cuadrada de la suma de a² y b².
¿Cuál es el resultado numérico de la distancia calculada en el video?
-El resultado numérico es de 4.73 unidades.
¿Por qué se utiliza el valor absoluto en la fórmula para calcular la distancia?
-El valor absoluto se utiliza para asegurar que la distancia sea un valor no negativo, independientemente del orden de los signos en la expresión.
¿Qué significa 'racionalizar' un resultado en el contexto del video?
-Racionalizar un resultado significa eliminar cualquier raíz en el denominador de una fracción, obteniendo así una expresión más simple y común en las matemáticas.
¿Cómo se racionaliza el resultado final en el ejemplo del video?
-Se multiplica el numerador y el denominador por la raíz cuadrada del mismo número (en este caso, 61) para eliminar la raíz en el denominador, dejando un resultado más simple.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Geometría analítica: Las rectas y sus ecuaciones

GEOMETRÍA ANALÍTICA desde CERO | ¿Qué es un SISTEMA COORDENADO?

DISTANCIA ENTRE 2 PUNTOS EN LA CIRCUNFERENCIA

Derivadas algebraicas y concepto preliminar de una diferencial - ROMATH

Definición de vector - MATEMÁTICAS
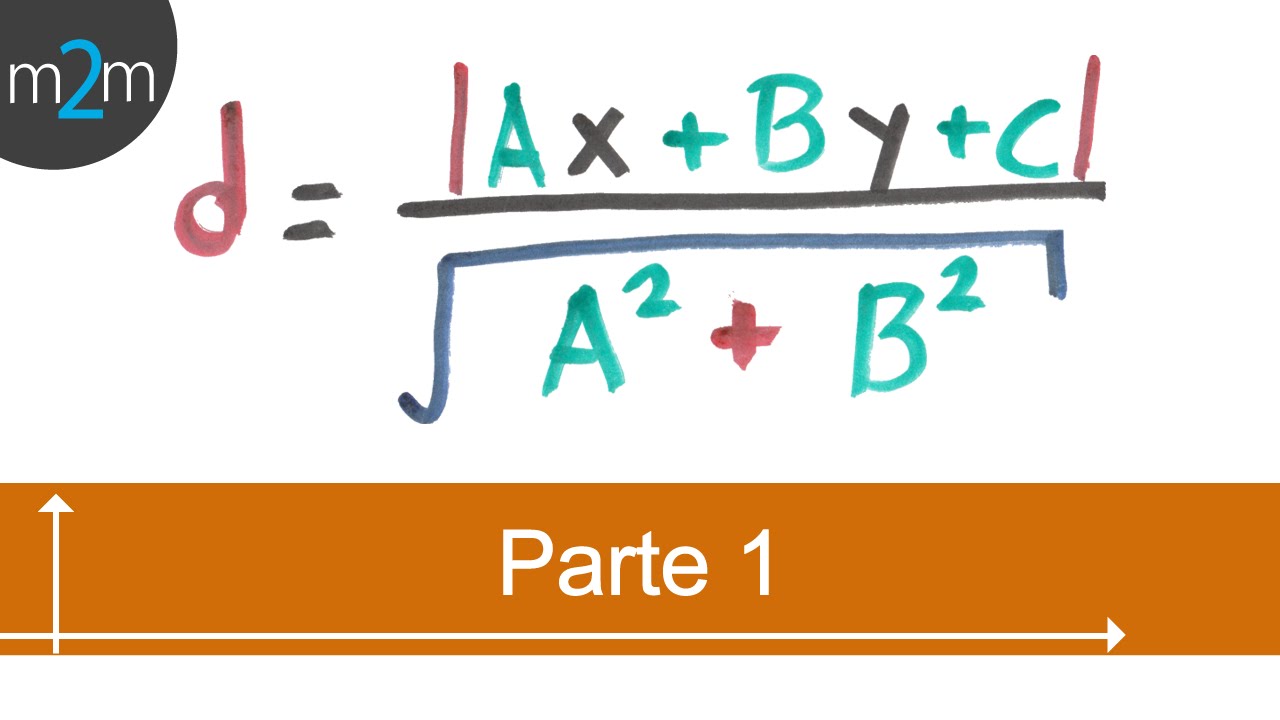
* Distancia entre un punto y una recta (PARTE 1)
5.0 / 5 (0 votes)
