Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geometry
Summary
TLDRThis instructional video script offers a comprehensive guide to calculating the areas of various geometric shapes, including rectangles, triangles, squares, circles, and more. It covers basic formulas for rectangles and triangles, introduces the concept of sectors and semi-circles in circles, and explains the area calculation for parallelograms, trapezoids, rhombuses, and scalene triangles. The script also touches on Heron's formula and the area of a circle with a known diameter or radius, providing a valuable resource for students of geometry.
Takeaways
- 📏 The area of a rectangle is found by multiplying its length by its width.
- 🔺 The area of a right triangle is calculated as one-half times the base times the height.
- 📐 For a non-right triangle, the area can be found using the formula: \( \frac{1}{2} \times \text{base} \times \text{height} \), where the height is the perpendicular distance from the base.
- 🔶 The area of an equilateral triangle is given by the formula: \( \frac{\sqrt{3}}{4} \times s^2 \), where \( s \) is the length of a side.
- 🔳 The area of a square is the length of one side squared.
- ⭕ To find the area of a circle, use the formula: \( \pi \times r^2 \), where \( r \) is the radius.
- 📉 The area of a sector of a circle is the fraction of the circle's angle over 360 degrees, times the area of the whole circle.
- 🏞 The area of a parallelogram is the base times the height.
- 🔸 For a trapezoid, the area is calculated as the average of the two bases times the height: \( \frac{1}{2} \times (b1 + b2) \times h \).
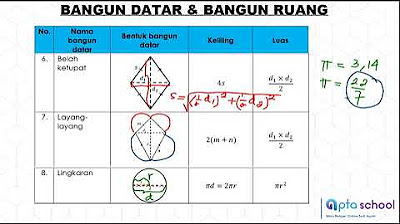
- 💠 The area of a rhombus is half the product of its diagonals: \( \frac{1}{2} \times d1 \times d2 \).
- 📐 Heron's formula can be used to find the area of a scalene triangle when all three sides are known: \( \sqrt{s(s-a)(s-b)(s-c)} \), where \( s \) is the semi-perimeter.
- 🔴 If given the diagonal of a square, the area can be found using the relationship between the diagonal and the side length in a 45-45-90 right triangle.
- 🌀 The area of a shaded region in a circle with a right triangle inside can be found by subtracting the area of the triangle from the area of the circle.
Q & A
What is the formula to calculate the area of a rectangle?
-The area of a rectangle is calculated by multiplying the length by the width (Area = Length × Width).
If the base of a right triangle is 10 and the height is 8, what is the area?
-The area of a right triangle is calculated as one half times the base times the height (Area = 1/2 × Base × Height). So, for a base of 10 and height of 8, the area is 40 square units.
How do you find the area of a triangle when you know the lengths of all three sides but it's not a right triangle?
-You can use Heron's formula, which is the square root of s(s - a)(s - b)(s - c), where s is the semi-perimeter of the triangle (s = (a + b + c) / 2), and a, b, and c are the lengths of the sides.
What is the formula for the area of an equilateral triangle?
-The area of an equilateral triangle is given by the formula (sqrt(3) / 4) × s², where s is the length of a side.
How is the area of a square calculated?
-The area of a square is found by squaring the length of one of its sides (Area = Side × Side or Area = Side²).
What is the formula to find the area of a circle?
-The area of a circle is calculated using the formula πr², where r is the radius of the circle.
If you have a sector of a circle with a 60-degree angle and a radius of 10, what is the area of the sector?
-The area of a sector is found by taking the fraction of the circle the sector represents (in this case, 60/360) and multiplying it by the area of the entire circle (πr²). So, the area is (60/360) × π × 10² = 50π/3 square units.
What is the area of a semi-circle with a radius of 8?
-The area of a semi-circle is half the area of a full circle, so it is (1/2)πr². With a radius of 8, the area is (1/2) × π × 8² = 32π square units.
How do you calculate the area of a parallelogram?
-The area of a parallelogram is calculated by multiplying the base by the height (Area = Base × Height).
What is the formula for the area of a trapezoid?
-The area of a trapezoid is found by taking the sum of the lengths of the two bases, multiplying by the height, and then dividing by two (Area = (Base1 + Base2) / 2 × Height).
How is the area of a rhombus determined?
-The area of a rhombus is calculated by taking half the product of the lengths of the diagonals (Area = 1/2 × Diagonal1 × Diagonal2).
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführen5.0 / 5 (0 votes)