Pencerminan/Refleksi 1| Transformasi Geometri

Summary

This video tutorial covers the concept of reflection transformations in geometry, specifically focusing on reflections across the x-axis, y-axis, y=x axis, and y=-x axis. The content is presented in an easy-to-understand manner, using practical examples to demonstrate how to reflect points and apply transformation matrices. It explains the basic properties of reflection, such as how the distance of the object point and the reflected image point are equal. The tutorial includes step-by-step demonstrations with specific examples, making complex concepts accessible and engaging for viewers.

Takeaways

• 😀 Reflection is a geometric transformation that moves an object to its mirrored position, maintaining equal distance from the mirror (e.g., flat mirror).
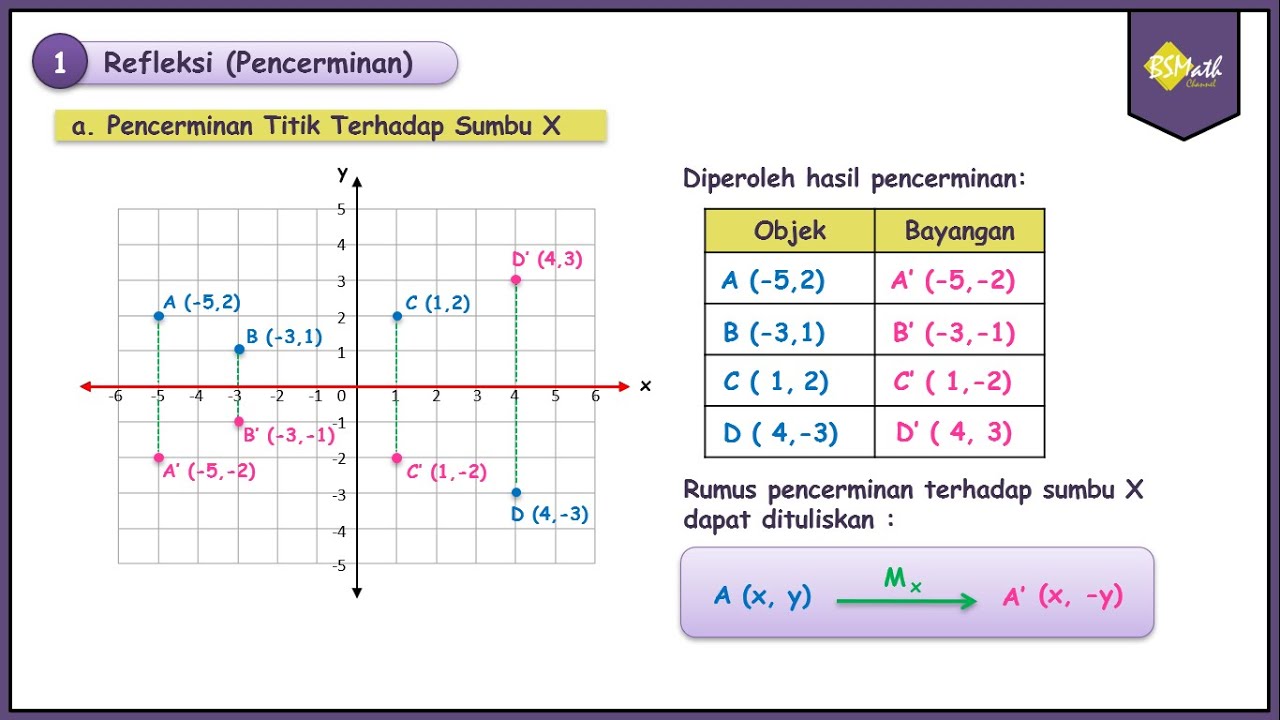
• 😀 Reflection on the x-axis means flipping a point across the x-axis, changing the y-coordinate's sign while keeping the x-coordinate the same.
• 😀 Example: Reflecting point (1,2) across the x-axis results in (1, -2).
• 😀 The reflection matrix for the x-axis is [1, 0; 0, -1], which can be applied to find the reflected image of any point.
• 😀 Reflection on the y-axis means flipping a point across the y-axis, changing the x-coordinate's sign while keeping the y-coordinate the same.
• 😀 Example: Reflecting point (2,1) across the y-axis results in (-2, 1).
• 😀 The reflection matrix for the y-axis is [-1, 0; 0, 1], which can be applied to find the reflected image of any point.
• 😀 Reflection on the line y = x swaps the x- and y-coordinates of a point.
• 😀 Example: Reflecting point (4,1) across the line y = x results in (1, 4).
• 😀 Reflection on the line y = -x involves swapping the coordinates and changing the signs of both x and y.
• 😀 Example: Reflecting point (4,1) across the line y = -x results in (-1, -4).

Q & A

What is the basic concept of reflection transformation as discussed in the video?

Reflection transformation is a geometric transformation that moves the position of an object to the position of its reflection, similar to how a flat mirror works. The distance from the object to the mirror is the same as the distance from the reflected point to the mirror.

How is reflection on the x-axis defined in the video?

Reflection on the x-axis means that the y-coordinate of a point is inverted, while the x-coordinate remains the same. For example, a point (x, y) reflected on the x-axis becomes (x, -y).

Can you provide an example of reflecting a point on the x-axis?

Yes, for example, if the point is (3, 5), when reflected on the x-axis, the resulting image will be (3, -5).

What is the reflection matrix for the x-axis and how is it used?

The reflection matrix for the x-axis is [[1, 0], [0, -1]]. This matrix is used by multiplying it with the coordinates of the point to find the image after reflection.

How is reflection on the y-axis different from the x-axis?

Reflection on the y-axis means the x-coordinate of a point is inverted, while the y-coordinate remains unchanged. For example, a point (x, y) reflected on the y-axis becomes (-x, y).

Could you explain the reflection matrix for the y-axis?

The reflection matrix for the y-axis is [[-1, 0], [0, 1]]. This matrix is applied to the coordinates of a point to reflect it over the y-axis.

How does the reflection on the line y = x work?

When reflecting a point on the line y = x, the x- and y-coordinates are swapped. For example, a point (x, y) reflected over y = x becomes (y, x).

Can you provide an example of reflecting a point over y = x?

Sure! If the point is (3, 5), reflecting it on the line y = x will give the result (5, 3).

What is the reflection matrix for the line y = x?

The reflection matrix for the line y = x is [[0, 1], [1, 0]]. Multiplying this matrix with the point’s coordinates swaps the values of x and y.

How does the reflection on the line y = -x work?

Reflection on the line y = -x means swapping the coordinates and negating both of them. A point (x, y) reflected over y = -x becomes (-y, -x).