TRANSFORMASI GEOMETRI || Matematika Kelas XI SMA
Summary
TLDRIn this educational video, Nuria Hasma Rifatul Ulya introduces the concept of geometric transformations, specifically focusing on reflection. Through the use of batik designs, such as Kawung, Silamtra, and Tambal, viewers are taught the principles of reflection across various axes and lines. The video explains how to reflect shapes across the x-axis, y-axis, lines y=x, y=-x, x=h, and y=k, with real-world examples of batik patterns. The viewer is guided through mathematical proofs, formulas, and sample problems, making learning both engaging and practical.
Takeaways
- 😀 The lesson introduces the concept of geometric transformations, specifically focusing on reflection using batik motifs.
- 😀 The importance of understanding reflection in geometry is highlighted, as it is applied to patterns in traditional batik designs.
- 😀 Reflection is demonstrated through batik examples like batik kawung, batik dlamprang, and batik tambal, each carrying symbolic meanings.
- 😀 Reflection across the x-axis, y-axis, and specific lines such as y = x and y = -x is explained with examples involving coordinates.
- 😀 The mathematical concept of reflection is linked to batik design, showcasing how geometric principles can be applied to real-world art.
- 😀 The reflection of coordinates is demonstrated with practical examples, showing how the coordinates change when reflected across different axes.
- 😀 Transformation matrices for reflections across the x-axis, y-axis, y = x, and y = -x are provided, with clear explanations of how to use them in calculations.
- 😀 Students are encouraged to solve problems involving reflections, such as determining the new coordinates of batik motifs after reflection.
- 😀 Reflection on lines other than the axes, such as x = h and y = k, is explored, with formulas for reflecting points across these lines.
- 😀 The session concludes with a summary of the main types of reflections and their impact on geometric figures, reiterating the connection between geometry and batik art.
Q & A
What is the main topic of the video script?
-The main topic of the video script is about understanding and applying the concept of geometric transformations, specifically reflections, through the context of batik patterns.
What are the main types of batik discussed in the script?
-The script discusses three main types of batik: Batik Kawung, Batik Silamtra, and Batik Tambal.
What does the Batik Kawung pattern symbolize?
-The Batik Kawung pattern symbolizes perfection, purity, and holiness. It originated in the 13th century in Yogyakarta.
How is reflection explained using Batik Kawung?
-Reflection is explained by showing how the Batik Kawung motif, when reflected across a line, results in a mirrored version of the pattern. For example, reflecting a pattern across the x-axis flips the coordinates vertically.
What is the role of matrices in the explanation of reflections?
-Matrices are used to mathematically represent the transformation of coordinates during reflections. The script uses specific transformation matrices for reflections across the x-axis, y-axis, y = x line, and y = -x line.
What happens when a point is reflected across the x-axis?
-When a point is reflected across the x-axis, its y-coordinate is inverted while the x-coordinate remains the same.
How does reflection work with respect to the line y = x?
-When a point is reflected across the line y = x, the coordinates of the point are swapped. For example, a point with coordinates (a, b) would be reflected to (b, a).
What is the significance of reflection against the line y = -x?
-Reflection against the line y = -x involves not only swapping the coordinates of the point but also negating them. Thus, a point (a, b) would reflect to (-b, -a).
What is the purpose of the example with Batik Jlamprang and the circle equation?
-The example with Batik Jlamprang and the circle equation demonstrates how reflections can be applied to more complex geometric shapes, such as circles, by reflecting their equations and finding the new centers after the reflection.
What is the result of reflecting a triangle with coordinates A(3,1), B(0,4), and C(6,4) across the line y = 1?
-After reflecting the triangle with coordinates A(3,1), B(0,4), and C(6,4) across the line y = 1, the new coordinates are A'(3,1), B'(0,-2), and C'(6,-2). The centroid of the triangle after reflection is (3, -1).
Outlines

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowMindmap

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowKeywords

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowHighlights

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowTranscripts

This section is available to paid users only. Please upgrade to access this part.
Upgrade NowBrowse More Related Video

Transformasi Geometri Bagian 3 - Rotasi (Putaran) Matematika Wajib Kelas 11
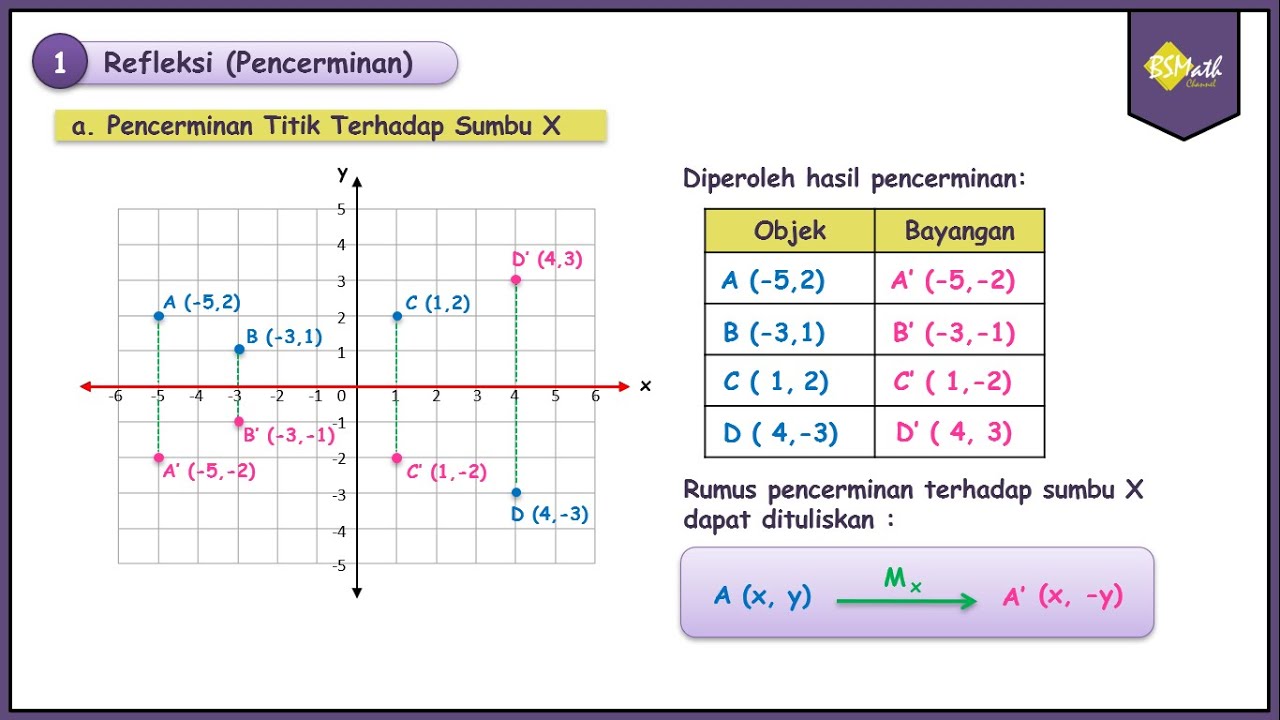
Transformasi Refleksi, Pencerminan Titik Terhadap Sumbu X - Matematika Tingkat Lanjut Kelas XI
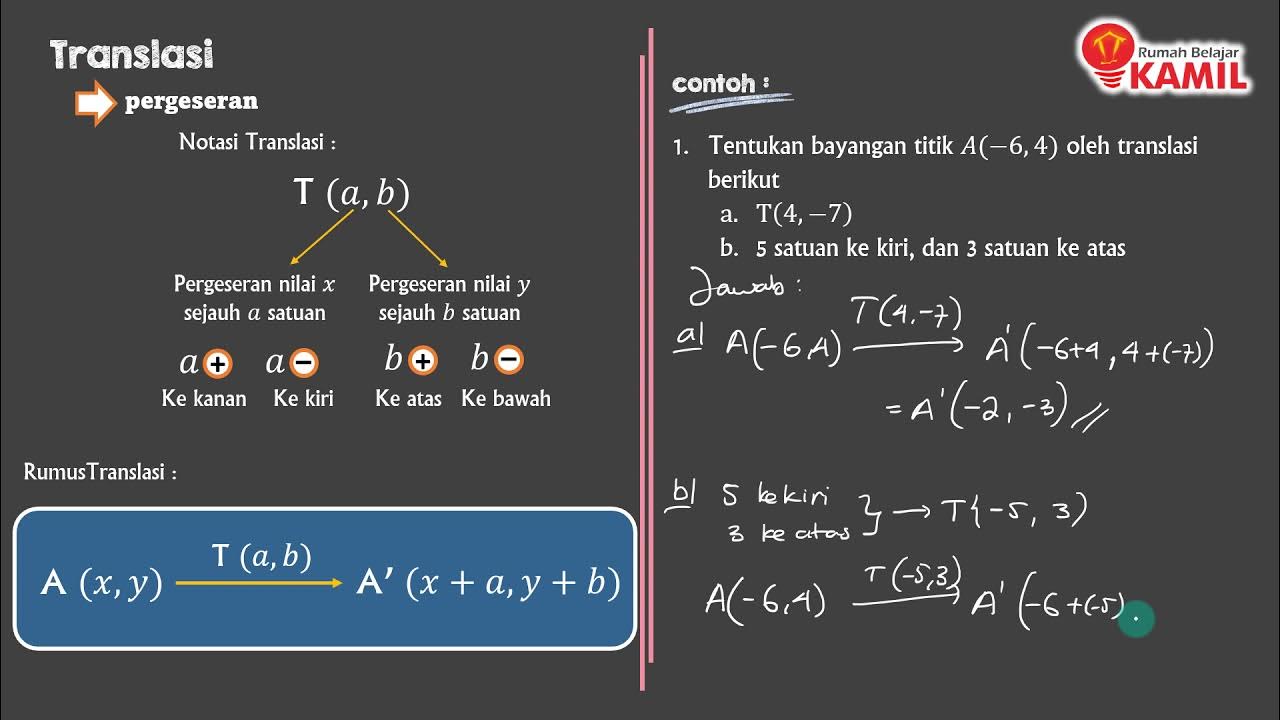
Matematika Kelas 9 : Transformasi Geometri (part 1 : Translasi)

Cara Cepat Memahami Transformasi Geometri [Matematika Kelas IX]

TRANSFORMAÇÕES ISOMÉTRICAS E HOMOTÉTICAS

TRANSFORMASI FUNGSI PART 1
5.0 / 5 (0 votes)