Sudut pada Dua Garis Sejajar Kelas 7

Summary

In this video, the concepts of angles formed by two parallel lines and a transversal are explained. The script covers the three possible positions of two lines (intersecting, perpendicular, and parallel), followed by an in-depth look at the various angles formed when two parallel lines are intersected by a transversal. These include adjacent, vertical, alternate interior, alternate exterior, and consecutive interior angles. Detailed examples are provided to demonstrate how to calculate the missing angle values, using relationships like supplementary and vertical angles. The video is both informative and instructional for solving geometry problems involving parallel lines.

Takeaways

• 😀 Two lines can have three possible relationships: intersecting, perpendicular, or parallel.
• 😀 Parallel lines, when extended, will never meet or intersect with each other.
• 😀 When two parallel lines are intersected by another line, they form 8 angles in total.
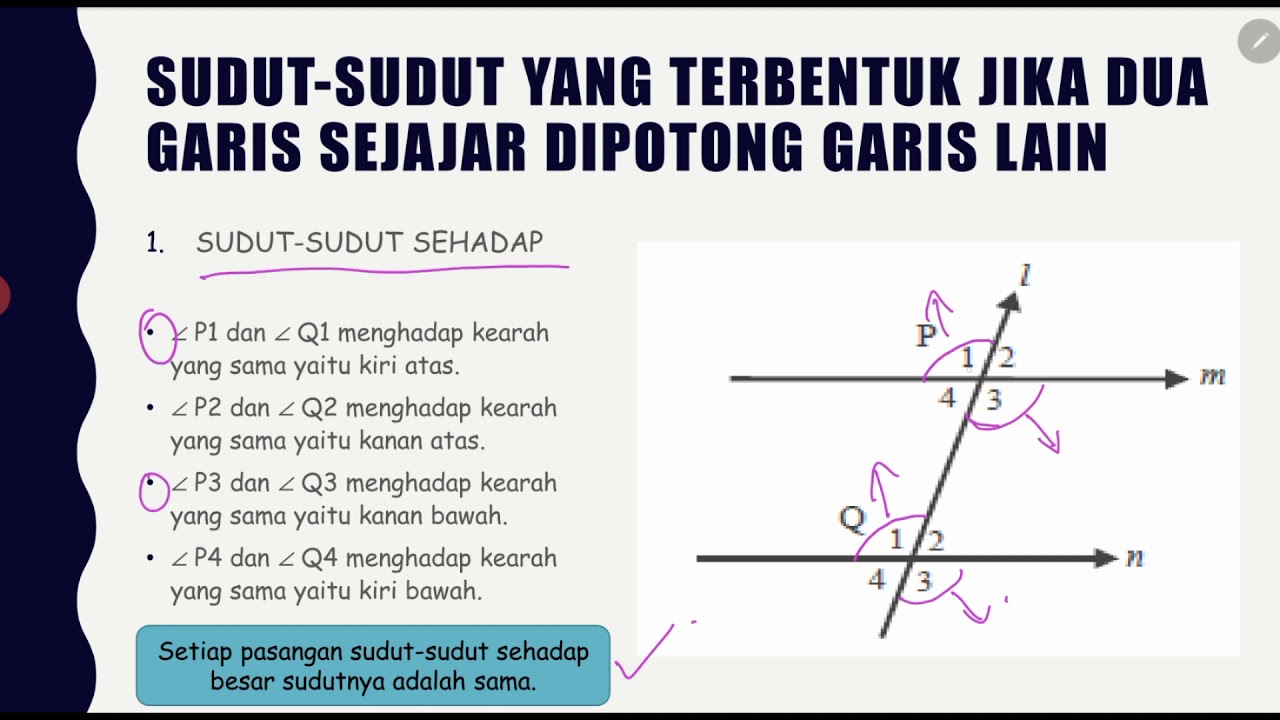
• 😀 Opposite angles (also called vertical angles) are equal. For example, angle 1 equals angle 5, angle 2 equals angle 6, etc.
• 😀 Angles that are opposite to each other across the intersection are called 'opposite' or 'vertical' angles, and they are always equal.
• 😀 Adjacent angles that share a common side and vertex can add up to 180° if they are supplementary.
• 😀 'Alternate interior angles' or 'alternate exterior angles' formed by parallel lines and a transversal are equal.
• 😀 'Consecutive interior angles' or 'same-side interior angles' add up to 180° when formed by a transversal cutting through parallel lines.
• 😀 The video provides practical examples for solving angle problems involving parallel lines, transversals, and the angle relationships mentioned.
• 😀 The script also includes step-by-step explanations for solving specific angle problems, such as finding unknown angles based on known ones, with calculations for angles like 110°, 70°, and more.

Q & A

What are the three possible positions that two lines can have in relation to each other?

The three possible relationships between two lines are: 1) The lines intersect at a point, 2) The lines are perpendicular to each other (forming a 90-degree angle), 3) The lines are parallel, meaning they never intersect no matter how far they are extended.

How are the angles formed when two parallel lines are cut by a transversal?

When two parallel lines are cut by a transversal, eight angles are formed. These angles include vertical angles, opposite angles, adjacent angles, and supplementary angles.

What are vertical angles, and how do they relate to each other?

Vertical angles are pairs of opposite angles formed when two lines intersect. These angles are always equal to each other. For example, if one angle measures 100°, its vertical angle will also be 100°.

What is the relationship between opposite angles in terms of their size?

Opposite angles (or vertical angles) are congruent, meaning they have the same measure. For example, if angle 1 is 100°, angle 5 (opposite angle) will also be 100°.

What are supplementary angles, and how are they related to each other?

Supplementary angles are two angles that add up to 180°. For example, if angle 1 measures 100°, angle 6 (which is supplementary to angle 1) will measure 80° to make the sum 180°.

What is the relationship between alternate interior angles when two parallel lines are intersected by a transversal?

Alternate interior angles are congruent when two parallel lines are intersected by a transversal. For example, if angle 2 measures 50°, then angle 7 will also measure 50°.

How do you calculate the measure of angle 2 if angle 1 is 110°?

To calculate angle 2, we use the fact that angles 1 and 2 are supplementary. Since their sum is 180°, we subtract 110° from 180° to find that angle 2 is 70°.

What is the method for finding the measure of angle 7 in this scenario?

To find angle 7, we can use the fact that it is either vertically opposite angle 1 or it can be considered as an exterior angle that is supplementary to angle 2. Either way, angle 7 will be 110°.

How can we calculate the value of x in the geometry problem involving angles A and B?

To calculate x, we first find angle A by using supplementary angles (180° - 110° = 70°). Then, we find angle B by using opposite angles (which are congruent). The value of x is the sum of angle A and angle B, which gives 70° + 50° = 120°.

How do you solve for angle x when two angles are supplementary and given specific angle measures?

If two angles are supplementary (their sum is 180°), and one angle is given as 50° and the other angle as 130°, we subtract 130° from 180° to find that the unknown angle x is 50°.