RazonesTrigonométricas
Summary
TLDREn este video de la Universidad de Costa Rica, se enseña a los estudiantes a identificar las razones trigonométricas de un triángulo rectángulo. Se explican los términos hipotenusa, cateto opuesto y cateto adyacente, y se definen las tres razones básicas: seno, coseno y tangente, junto con sus correspondientes razones recíprocas. Se utiliza el teorema de Pitágoras para encontrar la hipotenusa y se presentan ejemplos prácticos para calcular las razones trigonométricas y sus valores recíprocos. El video también sugiere practicar con ángulos en radianes para comprobar la consistencia de los resultados.
Takeaways
- 📚 Este video es una lección de matemáticas de la Universidad de Costa Rica sobre trigonometría en triángulos rectángulos.
- 🔍 Se identifican los términos clave: ángulo agudo (Alfa), hipotenusa (M), cateto opuesto (opuesto a Alfa) y cateto adyacente (unido a Alfa).
- 📐 Se definen las razones trigonométricas básicas: seno (freno), coseno y tangente, relacionadas con las medidas de los lados del triángulo.
- 🔄 Se presentan las razones trigonométricas recíprocas: cosecante, secante y cotangente, que son inversas a las razones básicas.
- 🧠 Se utiliza la técnica 'socatóa' para recordar las tres razones trigonométricas básicas por sus iniciales.
- 📘 Se hace un ejemplo práctico para aplicar la teoría, donde se calcula la hipotenusa utilizando el teorema de Pitágoras.
- 📝 Se calculan las seis razones trigonométricas para un triángulo rectángulo dado, usando las medidas de los catetos y la hipotenusa.
- 🔢 Se pide a los estudiantes que calculen los valores de X e Y en otro ejemplo, donde se conoce el ángulo y se debe usar la relación con las razones trigonométricas.
- 📐 Se sugiere que se compruebe la consistencia de los resultados al utilizar ángulos en radianes.
- 👍 Se agradece la atención y se anima a la práctica adicional para mejorar la comprensión de la trigonometría en triángulos rectángulos.
Q & A
¿Qué es un triángulo rectángulo y cómo se relaciona con la trigonometría?
-Un triángulo rectángulo es un triángulo que tiene un ángulo de 90 grados. En la trigonometría, se utilizan las relaciones entre los lados y los ángulos de este tipo de triángulo para definir las razones trigonométricas.
¿Cuáles son los nombres de los lados de un triángulo rectángulo en relación con un ángulo Alfa?
-El lado opuesto al ángulo de 90 grados se llama hipotenusa. El lado opuesto al ángulo Alfa se llama cateto opuesto, y el lado que une el ángulo Alfa con el ángulo de 90 grados es el cateto adyacente.
¿Qué son las razones trigonométricas y cómo se definen?
-Las razones trigonométricas son relaciones matemáticas entre los ángulos y los lados de un triángulo rectángulo. Se definen como: el seno de Alfa es el cateto opuesto dividido por la hipotenusa, el coseno de Alfa es el cateto adyacente dividido por la hipotenusa y la tangente de Alfa es el cateto opuesto dividido por el cateto adyacente.
¿Qué son las razones trigonométricas recíprocas y cómo se relacionan con las básicas?
-Las razones trigonométricas recíprocas son las que se generan a partir de las tres razones básicas. La cosecante es el inverso del seno, la secante es el inverso del coseno y la cotangente es el inverso de la tangente.
¿Cómo se puede recordar las tres razones trigonométricas básicas?
-Se puede utilizar el acrónimo 'SOCATOA', que se forma con las iniciales de cada una de las razones: seno, coseno, tangente, cotangente, secante y cosecante.
¿Qué herramienta matemática se utiliza para calcular la hipotenusa de un triángulo rectángulo si se conocen los catetos?
-Se utiliza el teorema de Pitágoras, que establece que el cateto al cuadrado más el cateto al cuadrado es igual a la hipotenusa al cuadrado.
En el ejemplo dado, ¿cómo se calcula la hipotenusa si los catetos miden 3 y 5 unidades?
-Para calcular la hipotenusa, se utiliza la fórmula dada por el teorema de Pitágoras: hipotenusa = √(cateto1^2 + cateto2^2). En este caso, hipotenusa = √(3^2 + 5^2) = √(9 + 25) = √34.
Si se conoce el valor de la hipotenusa y el cateto opuesto en un ángulo Alfa, ¿cuál es la fórmula para calcular el seno de Alfa?
-El seno de Alfa se calcula dividiendo el cateto opuesto por la hipotenusa: seno(Alfa) = cateto_opuesto / hipotenusa.
En el segundo ejemplo del guión, ¿qué información adicional se proporciona para determinar los valores de X y Y?
-En el segundo ejemplo, se proporciona la medida de un ángulo (30 grados), la hipotenusa y se pide determinar los valores de X (cateto opuesto) y Y (cateto adyacente) utilizando las razones trigonométricas apropiadas.
¿Cómo se puede utilizar la razón seno para determinar el valor de X en el segundo ejemplo del guión?
-Dado que X es el cateto opuesto al ángulo de 30 grados, se puede utilizar la fórmula del seno: seno(30°) = X / hipotenusa. Conociendo el valor de la hipotenusa, se puede despejar X.
¿Qué es un buen ejercicio para comprobar la consistencia de los resultados al utilizar ángulos en radianes?
-Un buen ejercicio es calcular las razones trigonométricas utilizando ángulos en radianes y comparar los resultados con los obtenidos utilizando ángulos en grados para asegurar que no varían.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
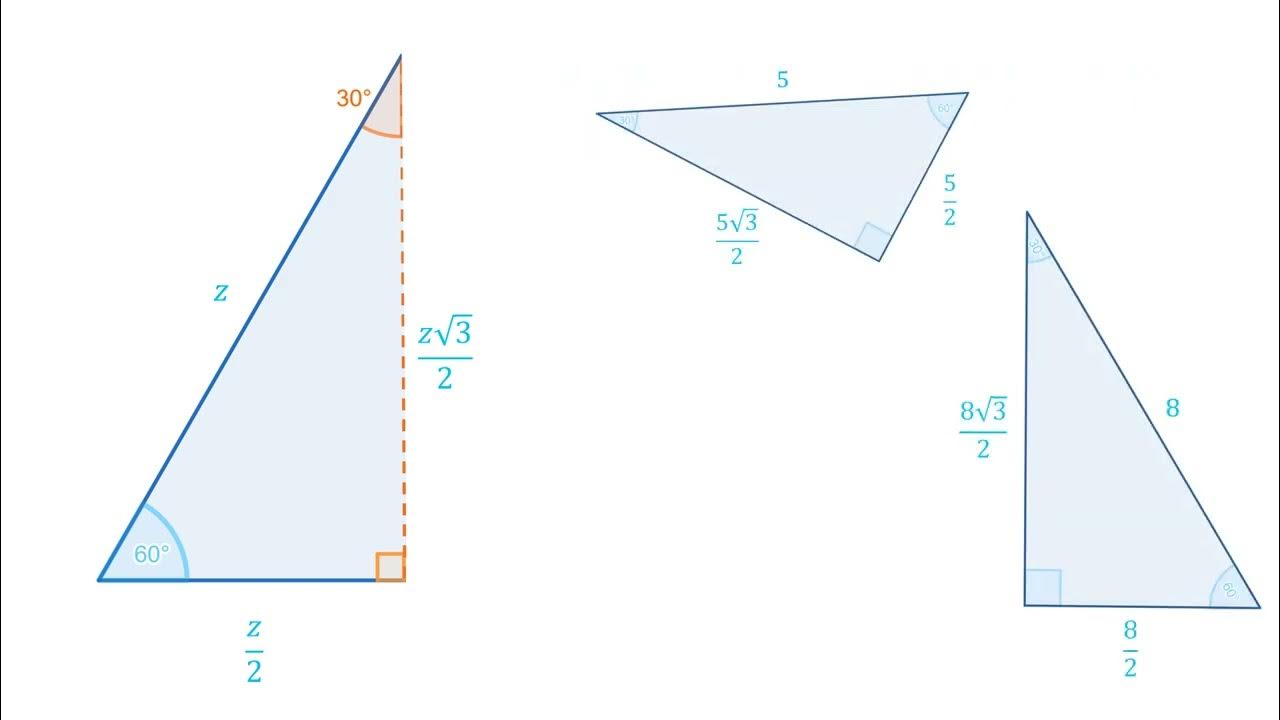
Razones Trigonométricas en Triángulos Especiales

Solucionar un triángulo rectángulo | Razones trigonométricas | Ejemplo 1
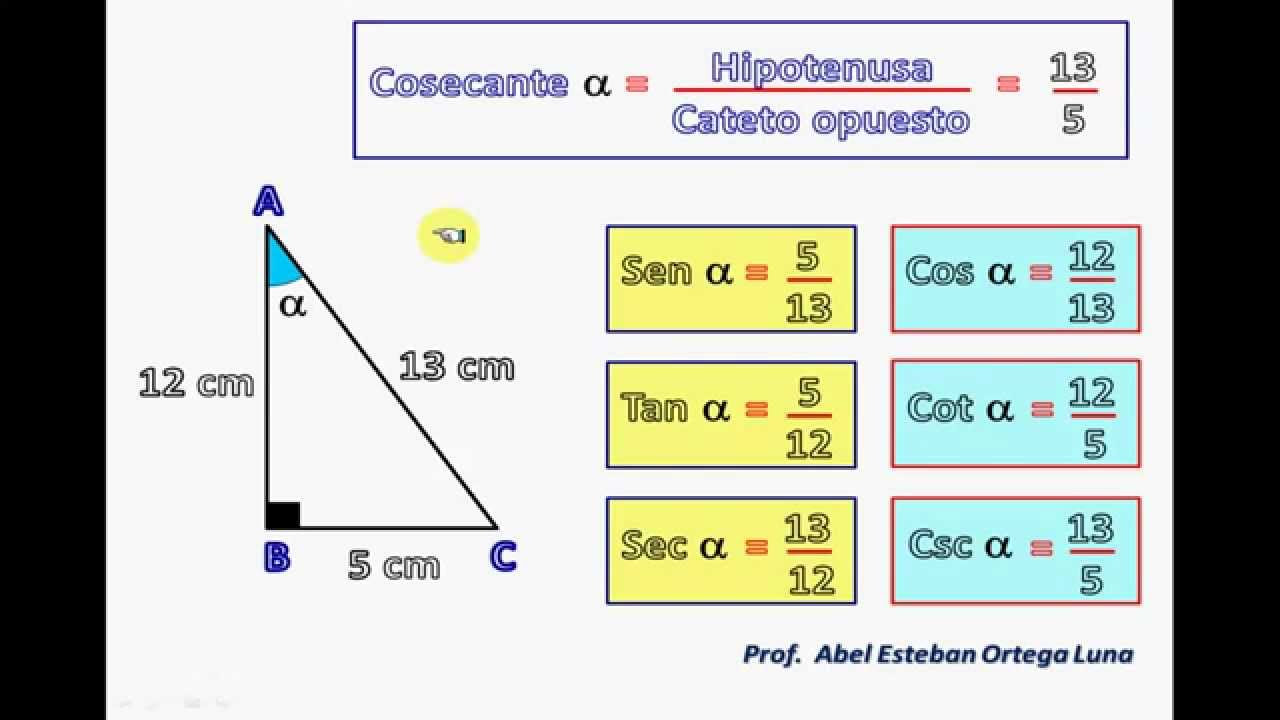
RAZONES TRIGONOMÉTRICAS EN UN TRIÁNGULO RECTÁNGULO

Razones trigonométricas de un ángulo | Ejemplo 1

Razones: elevación depresión

Como calcular los lados de un triángulo rectángulo conociendo un lado y un angulo
5.0 / 5 (0 votes)
